Phối Hợp Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim Bằng Mô Hình Cây Quyết Định

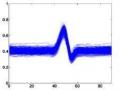
Trích kết quả của thuật toán phát hiện phức bộ QRS, thử nghiệm với bản ghi 100 trong bộ cơ sở dữ liệu MIT-BIH, kết quả thể hiện trên hình 3.6-f.

(a)

(b)

(c)

(d)

(e)

(f)

Hình 3.6. Ví dụ các bước phát hiện đỉnh R: (a) tín hiệu ECG gốc, (b) kết quả sau lọc,

(c) kết quả sau lấy đạo hàm, (d) kết quả sau lấy trị tuyệt đối, (e) kết quả sau khi lấy trung bình, (f) kết quả phát hiện đỉnh R.

3.1.2. Phân tích phức bộ QRS theo các hàm Hermite cơ sở

Phân tích tín hiệu điện tim theo hàm Hermite là một phương pháp khá phổ biến, đã được nhiều tác giả sử, kết quả đưa ra đều tốt và phương pháp này cũng là lựa chọn của luận văn. Trong mục này, tác giả sẽ trình bày quy trình tạo véc-tơ đặc tính của tín hiệu điện tim.

a) Hàm Hermite

Đa thức Hermite cho ở dạng đệ quy theo công thức sau:

Hn1 (x)  2x Hn (x)  2n Hn1 (x)

(3.6)

cho

n  1,

với

H0 (x)  1; H1(x)  2x.

Hàm Hermite được định nghĩa theo công thức sau:



n (x) 

 2nn!2e

x2

2 Hn (x)

1

(3.7)

Một số hình dạng của các hàm Hermite thể hiện trên hình 3.7. Ta thấy bậc của hàm Hermite càng cao thì tốc độ biến thiên của hàm càng lớn, hay nói cách khác hàm sẽ chứa nhiều các thành phần bậc càng cao. Đồng thời dáng điệu của các hàm cũng khá tương đồng với hình dạng các thành phần cơ bản trong tín hiệu ECG. Đây chính là cơ sở của việc sử dụng hàm Hermite để phân tích tín hiệu điện tâm đồ.

-10

-5	0	5	10 -10	-5	0	5	10
		(c)				(d)

Có thể bạn quan tâm!

• Một Số Mạng Nơ-Rôn Được Đề Xuất Để Ứng Dụng Nhận Dạng Tín Hiệu Điện Tim
• Thuật Toán Học Theo Bước Giảm Cực Đại Cho Mạng Mlp
• Xây Dựng Mô Hình Phối Hợp Các Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim
• Quy Trình Xây Dựng Cây Quyết Định Cho Khối Tổng Hợp Kết Quả
• Các Chỉ Tiêu Đánh Giá Chất Lượng Mô Hình Nhận Dạng Tín Hiệu Điện Tim
• Xây dựng mô hình phối hợp các mạng Nơ-rôn nhận dạng tín hiệu điện tim (ECG) - 11

Xem toàn bộ 98 trang tài liệu này.

-10 -5

0

(a)

5 10 -10 -5

0

(b)

5

10

Hình 3.7. Đồ thị của hàm Hermite bậc n: a) n=0, b) n=1, c) n=3, d) n=10.

Để biểu diễn một tín hiệu s(n) theo N hàm Hermite cơ sở đầu tiên, cần tìm các hệ số ci sao cho:

N 1

s(t) ci i (t)

i0

Khi ta có tín hiệu đã được số hóa, thay cho hàm thời gian

(3.8)

s(t) , ta có một chuỗi

p giá trị của tín hiệu tại các thời điểm (lấy mẫu) t0 ,t1, ,t p1 , khi đó các hệ số ci

chọn để thỏa mãn tốt nhất hệ phương trình sau:

được

c00 (t0 ) c11(t0 ) cN 1N 1(t0 ) s(t0 )

c (t ) c(t ) c (t ) s(t )

0 0 1 1 1 1

N 1

N 1 1 1



... ... ...

c00(t p) c11(t p) cN1N1(t p1) s(t p1)

với N=16, p=91. Hoặc chuyển sang dạng ma trận:

(3.9)

0 (t0 )

0 (t1)

1(t0 ) ...

1(t1) ...

N 1(t0 ) 

N 1(t1) 

c0 

c1 

s(t0 ) 

s(t1) 



 ... ... ... ... 

(t ) (t ) ... (t )c s(t )

0 p

Ta ký hiệu:

1 p N 1

p1 

N 1 

p1

 (3.10)

0 (t0 )

0 (t1 )

1 (t0 ) ...

1 (t1 ) ...

N 1 (t0 ) 

N 1 (t1 ) 

s(t0 ) c0 

s(t1 ) c1 

A  ;b  ; x 

 ... ... ... ... 

(t

) (t

) ... 

(t )s(t

)c

0

p1 1

p1

N 1

p1 

p1 

N 1 

Khi đó, hệ phương trình (3.10) sẽ có dạng ma trận:

A x b

hay

min

x

A x b

(3.11)

Các hệ số ci thỏa mãn tốt nhất hệ phương trình trên tương đương với việc đạt

cực tiểu của hàm sai số min

x

A x b . Thông thường, số liệu điểm lấy mẫu p=91 lớn

hơn so với số đa thức N=16 sử dụng để xấp xỉ nên đây là hệ phương trình có

nhiều phương trình hơn số ẩn. Nghiệm tối ưu của hệ phương trình có thể được xác định bằng việc sử dụng phương pháp phân tích theo các giá trị kỳ dị SVD (Singular Value Decomposition).

b) Sử dụng phương pháp SVD để xác định đặc tính tín hiệu điện tim

Để tìm nghiệm tối ưu của hệ phương trình bậc nhất có số phương trình nhiều

hơn số ẩn

A x b , như đã trình bày ở trên. Theo phương pháp SVD, trước tiên phân

tích ma trận A thành tích của 3 ma trận đặc biệt:

A pN

S pp VpN DT N

(3.12)

N

với S và D là các ma trận trực giao, V là ma trận đường chéo. Khi đó, ma trận

giả nghịch đảo



A

N p

của ma trận A có thể được xác định theo công thức:

AD VST

Np NN Np pp

(3.13)

với V+ là ma trận giả nghịch đảo của ma trận V, được xác định bằng cách thay các phần tử trên đường chéo của ma trận V bằng giá trị nghịch đảo, sau đó chuyển vị ma trận kết quả. Khi đã xác định được ma trận giả nghịch đảo A+ thì nghiệm x tối ưu

của hệ phương trình

A x b có thể được dễ dàng tính toán theo công thức:

x Ab (3.14)

Như đã trình bày ở phần trên, kết quả nghiệm x chính là các hệ số khai triển ci của tín hiệu điện tim ECG sẽ sử dụng làm các giá trị của véc-tơ đặc tính. Tín hiệu điện tim s t b có thể khôi phục lại theo công thức sau:

N 1

b ci i (t) b A x

i0

(3.15)

Trên hình 3.8 là một số ví dụ phân tích phức bộ QRS theo các hàm Hermite.

Trong đó, mầu xanh thể hiện là tín hiệu gốc

s t , mầu đỏ thể hiện tín hiệu xấp xỉ b.

Do tín hiệu

s t 

là tổ hợp của các hàm Hermite, số bậc Hermite càng cao thì sẽ biểu

diễn được các thành phần biến thiên nhanh, ví dụ như hình 3.8-a khi sử dụng ít hàm Hermite (N=5) thì chỉ biểu diễn được các thành phần biến thiên chậm và sai lệch khá lớn, còn khi sử dụng được nhiều hàm Hermite hơn ví dụ như các trường hợp N=10

(hình 3.8-b), N=12 (hình 3.8-c), N=16 (hình 3.8-d) thì biểu diễn tốt hơn rất nhiều, đặc biệt với N=16 sự trùng khít tương đối cao.

(a)

(b)

(c) (d)

Hình 3.8. Xấp xỉ tín hiệu ECG bằng N hàm Hermite cơ sở đầu tiên: a) N=5; b) N=10;

c) N=12; d) N=16.

Tuy nhiên việc lựa chọn số lượng hàm Hermite cũng cần phải khảo sát cụ thể, vì nếu sử dụng quá ít sẽ khiến cho mô hình nhận dạng bị thiếu hụt thông tin nên kết quả không chính xác, nếu sử dụng quá nhiều sẽ khiến cho mô hình trở nên cồng kềnh,

khối lượng tính toán lớn. Khảo sát sai số giữa tín hiệu gốc N hàm Hermite đầu tiên:

s tvà tín hiệu xấp xỉ theo

N 1

E s(t) cii (t)

i0

E 

s(t) b

(3.16)

20

Sai số E

10

0

4 8 12 14 16

Số lượng hàm Hermite N

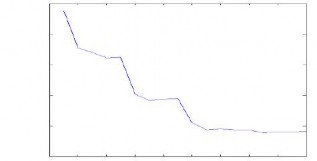
Hình 3.9. Đồ thị khảo sát sai số xấp xỉ theo số lượng các hàm Hermite cơ sở

Các biểu đồ khảo sát sai số E cho thấy khi tăng dần số lượng hàm Hermite để phân tích tín hiệu điện tim thì sai số E càng giảm, tức là càng trùng khít với tín hiệu gốc, trên hình 3.9 kết quả sai số ứng với số lượng hàm Hermite là N= 16 tiệm cận min,

nếu tiếp tục tăng số hàm Hermite thì sai số không giảm thêm được nhiều, do vậy luận văn đề xuất sử dụng trường hợp N=16.

Tiếp tục khảo sát khi khai triển sáu loại nhịp tim khác nhau theo 16 hàm Hermite, thể hiện trên hình 3.10 cho sử dụng hàm Hermite vẫn xấp xỉ khá tốt.

Tâm thất lỗi nhịp (E)

Block nhánh trái (L)

Block nhánh phải (R)

Ngoại tâm thu thất (V) Rung thất (I) Ngoại tâm thu nhĩ (A)

Hình 3.10. Hình ảnh khai triển các loại nhịp tím khác theo 16 hàm Hermite đầu tiên

c) Tạo véc-tơ đặc tính của tín hiệu điện tim ECG

,c15 ,RRlast ,RRmean 

18

- Theo quy trình trích chọn đặc tính tín hiệu điện tim ECG trong hình 2.4 ở mục

2.3, véc-tơ đặc tính gồm 18 thành phần:

x c0 ,

của mỗi nhịp (phức bộ QRS)

- 16 hệ số khai triển ci

i  0  15của tín hiệu điện tim ECG theo các hàm

Hermite như phương trình 3.9;

- 2 đặc tính trong miền thời gian của tín hiệu điện tim, là

RRlast khoảng cách

giữa hai đỉnh R liên tiếp (còn gọi là khoảng cách R-R), và

của 10 khoảng cách R-R cuối cùng.

3.2. Xây dựng các mô hình nhận dạng đơn

3.2.1. Quy trình xây dựng các mô hình đơn

RRmean giá trị trung bình

Trong luận văn, tác giả sử dụng bốn mô hình nhận dạng đơn, đó là các mô hình MLP, TSK, SVM và RF. Như đã trình bày ở trên, lý do sự lựa chọn các mô hình đơn này là:

- Trong các hệ thống tổng hợp ý kiến, số khối đơn vị thường phải lớn hơn hai

(để tránh trường hợp hai khối đưa ra kết quả trái ngược thì không biết nên theo kết

quả của khối nào). Hệ thống ba khối nhận dạng đơn là vừa đủ, không quá phức tạp cho các thử nghiệm trong luận văn;

- Các mạng được lựa chọn đều là các mạng kinh điển, đã được sử dụng trong rất nhiều ứng dụng xử lý tín hiệu nói chung và trong các bài toán nhận dạng nói riêng;

Sau đây, sẽ lần lượt giới thiệu tóm tắt về cấu trúc, thuật toán xây dựng các mạng dựa trên các quá trình học của bốn mạng cơ sở này.

3.2.2. Xây dựng mô hình mạng MLP

Lựa chọn cấu trúc một mạng MLP có một lớp ẩn, có cấu trúc như trong [6].

Quy trình huấn luyện (học) cho mạng nơ-rôn MLP như sau:

- Đầu tiên, khởi tạo các giá trị ban đầu của mạng nơ-rôn MLP như ma trận trọng số W, V và số nơ-rôn ẩn M. Tăng dần số nơ-rôn ẩn M từ 1 cho tới khi đạt được độ chính xác mong muốn, luận văn tìm M trong khoảng từ 1 đến 30;

- Tiếp theo, là quá trình điều chỉnh thích nghi (quá trình học) để hiệu chỉnh các trọng số ghép nối giữa các lớp của mạng MLP là ma trận trọng số W, ma trận trọng số V, trong luận văn sử dụng thuật toán bước giảm cực đại;

- Kiểm tra sai số học, nếu đạt thì dừng lại, ngược lại quay lại bước đầu tiên để tăng số nơ-rôn ẩn. Quá trình huấn luyện dừng khi sai số đạt yêu cầu đặt ra;

- Kiểm tra mô hình huận luyện được bằng bộ mẫu kiêm tra, đánh giá sai số.

3.2.3. Xây dựng mô hình mạng TSK

Tương tự như với mạng nơ-rôn MLP, với mạng nơ-rôn là tăng số nơ-rôn ẩn M còn với mạng logic mờ TSK là số luật, trong luận văn số luật được tìm từ 1 đến 25 luận, cấu trúc của mạng TSK như trong [5, 6], cụ thể:

- Khởi tạo các giá trị ban đầu của các tham số tuyến tính và phi tuyến, đặt số luật khởi điểm;

- Điều chỉnh các tham số tuyến tính và phi tuyến, luận văn sử dụng thuật toán lặp sử dụng bước giảm cực đại của hàm gradient;

- Kiểm tra sai số học, nếu đạt thì dừng lại, ngược lại quay lại bước 1 tăng số luật. Quá trình huấn luyện dừng khi sai số đạt yêu cầu đặt ra;

- Kiểm tra mô hình huận luyện được bằng bộ mẫu kiêm tra, đánh giá sai số.

3.2.4. Xây dựng mô hình véc-tơ hỗ trợ SVM

Quy trình xây dựng mô hình nhận dạng dùng máy hỗ trợ véc-tơ SVM có khác so với hai mô hình trên. Như đã trình bày ở trên, do mô hình SVM chỉ là phân lớp nhị phân (hai lớp), nếu đối với các bài toán phân loại nhiều lớp (lớn hơn hai lớp) thì cần cải tiến thành các mô hình SVM đa lớp, hiện nay có nhiều phương pháp để xây dựng mô hình SVM đa lớp, trong luận văn lựa chọn phương án một chọi một

(Onevesus–One), tức là nếu phân loại N lớp thì cần xây dựng tất cả mô hình

SVM nhị phân, chúng được kết nối lại với nhau và thông qua phương pháp bỏ phiếu để đánh giá kết quả phân lớp cuối cùng, lớp nào có số phiếu nhiều nhất sẽ được chọn làm kết quả dự đoán.

3.2.5. Mô hình rừng ngẫu nhiên RF

Mô hình nhận dạng đơn cuối cùng dùng trong luận án là mô hình rừng ngẫu nhiên RF (Random Forest) được phát triển từ L. Breiman (2001) [19]. RF và SVM là hai giải thuật học nhanh, chịu nhiễu tốt, các bước xây dựng chính:

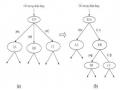
- Xây dựng rừng ngẫu nhiên RF (được mô tả trong hình 3.11) tạo ra một tập hợp M cây quyết định không cắt nhánh, mỗi cây được xây dựng trên tập mẫu bootstrap (lấy mẫu ngẫu nhiên có hoàn lại);

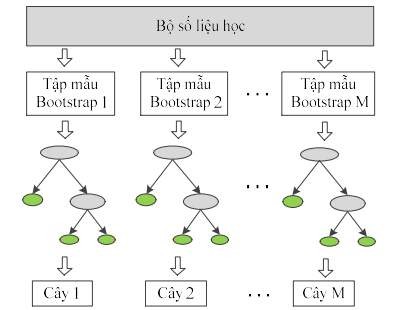
Hình 3.11. Quá trình xây dựng các cây quyết định thành phần

X

Cây 1

Bộ số liệu học/ kiểm tra

Cây 2

Cây M

y1

y2

Kết quả học/ kiểm tra

yM

Khối tổng hợp kết quả (phương pháp bỏ phiếu)

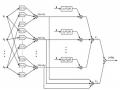
- Khâu tổng hợp các kết quả nhận dạng từ M cây quyết định phổ biến sử dụng phương pháp bỏ phiểu theo đám đông để đưa ra kết quả cuối cùng, như trong hình 3.12.

Hình 3.12. Quá trình kiểm tra của mô hình rừng ngẫu nhiên RF

3.3. Phối hợp mạng nơ-rôn nhận dạng tín hiệu điện tim bằng mô hình cây quyết định

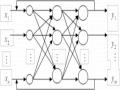
3.3.1. Đề xuất mô hình kết hợp

Hình 3.13 biểu diễn sơ đồ chung của mô hình kết hợp sử dụng nhiều mô hình nhận dạng đơn, trong đó, M  số mô hình nhận dạng đơn, xin  tín hiệu điện tim ECG đầu vào, Pi  là các khối tiền xử lý và trích chọn đặc tính, Ci  các khối phân loại, z kết quả nhận dạng cuối cùng tương ứng với tín hiệu đầu vào xin .

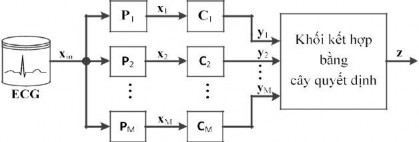
Hình 3.13. Sơ đồ chung của mô hình kết hợp sử dụng nhiều mô hình nhận dạng đơn

Nhìn chung, các mô hình nhận dạng cơ sở làm việc độc lập với tín hiệu điện tim đầu vào xin có thể từ các chuyển đạo khác nhau, các khối tiền xử lý và trích chọn đặc tính Pi dùng các phương pháp khác nhau. Như đã trình bày ở phần mở đầu, định hướng nghiên cứu của luận văn là sử dụng chung một phương pháp tiền xử lý và trích chọn đặc tính P1  P2  ...  PM  cho các mô hình nhận dạng đơn Ci.

Nếu bài toán nhận dạng K loại nhịp tim khác nhau, thì mỗi mô hình nhận dạng đơn Ci (với i=1, 2,…, M) sẽ có M kết quả yi (với i=1, 2,…, M) biểu diễn dưới dạng véc-tơ (công thức 3.1), một véc-tơ yi lý tưởng khi có một giá trị bằng ‘1’ và tất cả các giá trị còn lại đều bằng ‘0’, nhưng thông thường các giá trị của chúng thường dao động trong khoảng [0, 1]. Trong luận văn, các kết quả đầu ra yi từ các mô hình nhận dạng cơ sở được hợp lại thành một véc-tơ tổng Y (có kích thước M- K) như (3.2) và được tiếp tục xử lý tại khối kết hợp kết quả để đưa ra kết luận cuối cùng là véc-tơ z (có kích thước K) tương ứng với mã của K loại nhịp tim khác nhau.

- Kết quả của mô hình nhận dạng đơn Ci (với i=1, 2,…, M):

yi yi1 yi2 ... yiK (3.17)

- Véc-tơ tổng hợp:

Y = [y1 y2 ... yM]

= [y11y12...y1K y21y22...y2K ... yM1yM2...yMK] (3.18)

Một số giải pháp kết hợp kết quả thông dụng đã được nhiều nghiên cứu khác đề xuất: Biểu quyết theo đa số [11, 16], biểu quyết có trọng số [28, 34], tổng hợp theo xác suất điều kiện Bayes [28]… Nhìn chung các giải pháp này khá đơn giản, ổn định, hiệu

Xem tất cả 98 trang.