Một Số Mạng Nơ-Rôn Được Đề Xuất Để Ứng Dụng Nhận Dạng Tín Hiệu Điện Tim

Hàm kích hoạt hay còn được gọi là hàm nén vì chúng nén tín hiệu đầu ra vào một khoảng nhỏ. Hàm kích hoạt hay được sử dụng là:

- Gồm một tập các đơn vị xử lý (các nơ-rôn nhân tạo) - Trạng thái kích hoạt hay đầu ra của đơn vị xử lý - Liên kết giữa các đơn vị. Xét tổng quát, mỗi liên kết được định nghĩa bởi một trọng số Wjk cho ta biết hiệu ứng mà tín hiệu của đơn vị j có trên đơn vị k - Một luật lan truyền quyết định cách tính tín hiệu ra của từng đơn vị từ đầu vào của nó - Một hàm kích hoạt, hay hàm chuyển (activation function, transfer function), xác định mức độ kích hoạt khác dựa trên mức độ kích hoạt hiện tại - Một đơn vị điều chỉnh (độ lệch) (bias, offset) củ a mỗi đơn vị - Phương pháp thu thập thông tin (luật học - learning rule) - Môi trường hệ thống có thể hoạt động.

* Định nghĩa mạng nơ-rôn nhân tạo

Hiện vẫn chưa có một định nghĩa tổng quát nào về mạng nơ-rôn, song phần lớn những người làm việc trong lĩnh vực mạng nơ-rôn đều có thể đồng ý với định nghĩa sau [3]: “Mạng nơ-rôn là một hệ thống gồm nhiều phần tử xử lý đơn giản gọi là các nơ-rôn được liên kết với nhau và cùng hoạt động song song. Tính năng hoạt động của mạng phụ thuộc vào cấu trúc mạng, trọng số liên kết giữa các nơ-rôn và quá trình xử lý bên trong các nơ-rôn. Ngoài chức năng xử lý, hệ thống còn có khả năng học số liệu và tổng quát hóa từ các số liệu đã học”.

Những mô hình mạng nơ-rôn có tiềm năng tạo nên một cuộc cách mạng trong công nghệ máy tính và các quá trình xử lý thông tin. Nhận xét đó hoàn toàn có cơ sở và chủ yếu bắt nguồn từ các đặc trưng chính sau của mạng nơ-rôn:

- Một là, tính chất phi tuyến. Đây là một tính chất này rất quan trọng. Mạng nơ- rôn nhân tạo có thể tính toán một cách tuyến tính hay phi tuyến. Nó cho phép mạng nơ-rôn tạo ra các mặt cắt trong không gian dữ liệu không phải là siêu phẳng mà lồi lòm không đều. Như vậy không gian mẫu có thể chia thành nhiều miền. Mỗi miền được gọi là một lớp. Đặc trưng này được sử dụng nhiều, ví dụ trong xấp xỉ mạng, miền nhiễu và có khả năng phân lớp.

- Hai là, tự thích nghi và tự tổ chức. Các mạng nơ-rôn có khả năng xử lý thích nghi và điều chỉnh bền vững dựa vào các thuật toán học và quy tắc tự tổ chức. Khả năng xử lý thích nghi thể hiện ở khả năng biến đổi các trọng số trong mạng tuỳ theo sự thay đổi của môi trường xung quanh. Một mạng nơ-rôn đã được huấn luyện trong môi trường xác định, vẫn có thể thích nghi trong môi trường khác bằng cách tự thay đổi trọng số các kết nối. Vì vậy dù mẫu không ổn định hay bị nhiễu thì nó vấn có thể đáp ứng thích hợp. Tuy nhiên, không phải lúc nào tính tự thích nghi cũng mang lại hiệu quả hay sức mạnh cho mạng.

- Ba là, tính chịu lỗi. Não của con người có khả năng dung thứ lỗi, tức là với những thông tin thiếu chính xác, không đầy đủ mà vẫn có thể xử lý, giải quyết được các vấn đề đặt ra. Mạng nơ-rôn bắt chước khả năng này của bộ não. Hệ thống mạng nơ-rôn vẫn có thể tiếp tục hoạt động và điều chỉnh, khi nhận tín hiệu vào có một

Có thể bạn quan tâm!

• Xây dựng mô hình phối hợp các mạng Nơ-rôn nhận dạng tín hiệu điện tim (ECG) - 2
• Tổng Quan Về Các Phương Pháp Nhận Dạng Tín Hiệu Điện Tim‌
• Định Hướng Nghiên Cứu Của Đề Tài
• Thuật Toán Học Theo Bước Giảm Cực Đại Cho Mạng Mlp
• Xây Dựng Mô Hình Phối Hợp Các Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim
• Phối Hợp Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim Bằng Mô Hình Cây Quyết Định

Xem toàn bộ 98 trang tài liệu này.

phần thông tin bị sai lệch hay bị thiếu. Khi một số nơ-rôn không thực hiện tính toán, hay một vài kết nối bị hỏng thì khả năng của mạng chỉ bị giảm đi chứ không bị đổ vỡ. Mạng nơ-rôn luôn đưa ra kết quả thích hợp trong mọi tình huống.

- Bốn là, tính đồng dạng trong thiết kế. Các mô hình mạng nơ-rôn đều có chung đặc điểm là được cấu thành từ các nơ-rôn riêng biệt liên kết với nhau. Liên kết càng phức tạp thì mô hình mạng nơ-rôn càng mạnh. Các mạng tổ hợp có thể xây dựng bằng cách tích hợp nhiều mạng khác nhau.

Với những tiềm năng to lớn ANN thực sự đã và đang mang lại rất nhiều lợi ích cho cuộc sống của con người và chứng minh sức mạnh của nó.

2.3.3. Các hàm kích hoạt

Phần lớn các đơn vị trong mạng nơ-rôn chuyển net input bằng cách sử dụng một hàm vô hướng (scalar-to-scalar function) gọi là hàm kích hoạt, kết quả của hàm này là một giá trị gọi là mức độ kích hoạt của đơn vị (unit's activation). Loại trừ khả năng đơn vị đó thuộc lớp ra, giá trị kích hoạt được đưa vào một hay nhiều đơn vị khác. Các hàm kích hoạt thường bị ép vào một khoảng giá trị xác định, do đó thường được gọi là các hàm bẹp (squashing). Các hàm kích hoạt hay được sử dụng là:  Hàm đồng nhất (Linear function, Identity function )

g(x)=x (2.4)

Nếu coi các đầu vào là một đơn vị thì chúng sẽ sử dụng hàm này. Đôi khi một hằng số được nhân với net-input để tạo ra một hàm đồng nhất.

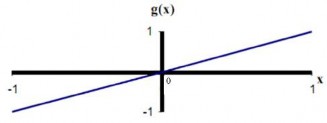
Hình 2.6. Hình hàm đồng nhất

Hàm bước nhị phân (Binary step function, Hard limit function) Hàm này cũng được biết đến với tên "Hàm ngưỡng" (Threshold function hay Heaviside function). Đầu ra của hàm này được giới hạn vào một trong hai giá trị:

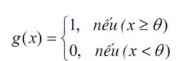(2.5)

Dạng hàm này được sử dụng trong các mạng chỉ có một lớp. Trong hình vẽ sau, θ được chọn bằng 1.

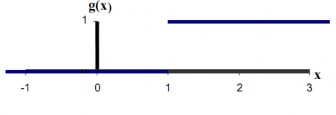
Hình 2.7. Hàm bước nhị phân (Binary step function)

Hàm sigmoid (Sigmoid function (logsig))

(2.6)

Hàm này đặc biệt thuận lợi khi sử dụng cho các mạng được huấn luyện (trained) bởi thuật toán Lan truyền ngược (back-propagation), bởi vì nó dễ lấy đạo hàm, do đó có thể giảm đáng kể tính toán trong quá trình huấn luyện. Hàm này được ứng dụng cho các chương trình ứng dụng mà các đầu ra mong muốn rơi vào khoảng [0,1].

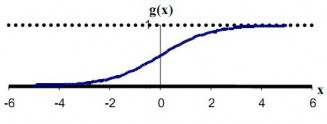
Hình 2.8. Hàm Sigmoid

Hàm sigmoid lưỡng cực (Bipolar sigmoid function (tansig))

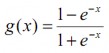(2.7)

Hàm này có các thuộc tính tương tự hàm sigmoid. Nó làm việc tốt đối với các ứng dụng có đầu ra yêu cầu trong khoảng [-1,1].

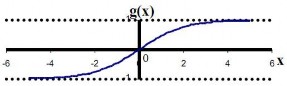
Hình 2.9. Hàm sigmoid lưỡng cực

Hàm chuyển của các đơn vị ẩn (hidden units) là cần thiết để biểu diễn sự phi tuyến vào trong mạng. Lý do là hợp thành của các hàm đồng nhất là một hàm đồng nhất. Mặc dù vậy nhưng nó mang tính chất phi tuyến (nghĩa là, khả năng biểu diễn các hàm phi tuyến) làm cho các mạng nhiều tầng có khả năng rất tốt trong biểu diễn các ánh xạ phi tuyến. Tuy nhiên, đối với luật học lan truyền ngược, hàm phải khả vi (differentiable) và sẽ có ích nếu như hàm được gắn trong một khoảng nào đó. Do vậy, hàm sigmoid là lựa chọn thông dụng nhất. Đối với các đơn vị đầu ra (output units), các

hàm chuyển cần được chọn sao cho phù hợp với sự phân phối của các giá trị đích mong muốn. Chúng ta đã thấy rằng đối với các giá trị ra trong khoảng [0,1], hàm sigmoid là có ích; đối với các giá trị đích mong muốn là liên tục trong khoảng đó thì hàm này cũng vẫn có ích, nó có thể cho ta các giá trị ra hay giá trị đích được căn trong một khoảng của hàm kích hoạt đầu ra. Nhưng nếu các giá trị đích không được biết trước khoảng xác định thì hàm hay được sử dụng nhất là hàm đồng nhất (identity function). Nếu giá trị mong muốn là dương nhưng không biết cận trên thì nên sử dụng một hàm kích hoạt dạng mũ (exponential output activation function).

2.3.4. Phân loại các mạng nơ-rôn

Liên kết các đầu vào và ra của nhiều nơ-rôn với nhau ta được một mạng nơ-rôn. Nguyên lý cấu tạo của một mạng nơ-rôn bao gồm một hoặc nhiều lớp. Mỗi lớp bao gồm nhiều nơ-rôn có cùng một chức năng trong mạng. Dựa vào số lớp hay sự liên kết giữa các lớp trong mạng mà người ta phân mạng nơ-rôn nhân tạo thành các nhóm khác nhau.

* Phân loại theo số lớp

Dựa theo số lớp thì mạng nơ-rôn gồm hai loại: mạng một lớp và mạng nhiều lớp.

- Mạng một lớp: Mạng một lớp cấu thành từ một lớp mạng, nó vừa là lớp vào vừa là lớp ra.

y1

y2

ym

x1

x2

- Mạng nhiều lớp

xn

Hình 2.10. Mô hình mạng nơ-rôn một lớp

Mạng nhiều lớp được cấu thành từ nhiều lớp liên kết với nhau, bao gồm một lớp vào, lớp ẩn và một lớp ra. Trong đó, lớp nhận tín hiệu đầu vào được gọi là lớp vào. Các tín hiệu đầu ra của mạng được sản sinh bởi lớp ra của mạng. Các lớp nằm giữa lớp vào và lớp ra được gọi là lớp ẩn. Lớp ẩn là thành phần nội tại của mạng, nó không có bất kỳ tiếp xúc nào với môi trường bên ngoài. Số lượng lớp ẩn có thể dao động từ 0 đến một vài lớp. Tuy nhiên, thực tế cho thấy chỉ cần một lớp ẩn là mạng đã đủ để giải quyết được một lớp các bài toán phức tạp nào.

lớp vào

lớp

ẩn

lớp ra

Hình 2.11. Mô hình mạng nơ-rôn 3 lớp truyền thẳng

* Phân loại theo sự liên kết giữa các lớp

Sự liên kết trong mạng nơ-rôn tuỳ thuộc vào nguyên lý tương tác giữa đầu ra của từng nơ-rôn riêng biệt với nơ-rôn khác và tạo ra cấu trúc mạng nơ-rôn. Về nguyên tắc sẽ có rất nhiều kiểu liên kết giữa các nơ-rôn, nhưng chỉ có một số cấu trúc hay gặp trong ứng dụng sau:

- Mạng truyền thẳng (Feedforward neural networks)

Dòng dữ liệu đầu vào từ các nơ-rôn đầu vào đến các nơ-rôn đầu ra chỉ được truyền thẳng. Việc xử lý dữ liệu có thể mở rộng ra nhiều lớp, nhưng không có các liên kết ngược. Tức là, không có các liên kết từ các đơn vị đầu ra tới các đơn vị đầu vào trong cùng một lớp hay các lớp trước đó.

Nếu mô hình hoá mạng truyền thẳng bằng một đồ thị, thì nó là một đồ thị có hướng hữu hạn không chu trình. Trong đó, mỗi nơ-rôn là một nút, các liên liên kết giữa các nơ-rôn là các cung của đồ thị. Hình 2.11 là một minh họa về mạng truyền thẳng nhiều lớp.

- Mạng hồi quy (mạng nối ngược) (Recurrent neural network)

Khác với mạng truyền thẳng, mạng hồi quy có chứa các liên kết ngược. Mô hình hoá mạng hồi quy bằng một đồ thị thì nó là một đồ thị có hướng hữu hạn có chu trình. Hình 2.12 minh họa cho một mạng hồi quy.

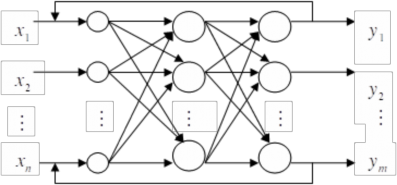
Hình 2.12. Mô hình mạng nơ-rôn 3 lớp hồi quy

2.4. Huấn luyện mạng nơ-rôn

Chức năng của một mạng nơ-rôn được quyết định bởi các nhân tố như: hình trạng mạng (số lớp, số đơn vị trên mỗi tầng và cách mà các lớp được liên kết với nhau) và các trọng số của các liên kết bên trong mạng. Hình trạng của mạng thường là cố định và các trọng số được quyết định bởi một thuật toán huấn luyện (training algorithm). Tiến trình điều chỉnh các trọng số để mạng “nhận biết” được quan hệ giữa đầu vào và đích mong muốn được gọi là học (learning) hay huấn luyện (training). Rất nhiều thuật toán học đã được phát minh để tìm ra tập trọng số tối ưu làm giải pháp cho các bài toán. Các thuật toán đó có thể chia làm hai nhóm chính: Học có thầy (Supervised learning) và Học không có thầy (Unsupervised Learning).

- Học có thầy (Supervised learning):

Hình 2.13 là mô hình học có thầy. Mạng được huấn luyện bằng cách cung cấp cho nó các cặp mẫu đầu vào và các đầu ra mong muốn (target values). Các cặp được cung cấp bởi "thầy giáo", hay bởi hệ thống trên đó mạng hoạt động. Sự khác biệt giữa các đầu ra thực tế so với các đầu ra mong muốn được thuật toán sử dụng để thích ứng các trọng số trong mạng. Điều này thường được đưa ra như một bài toán xấp xỉ hàm số

- cho dữ liệu huấn luyện bao gồm các cặp mẫu đầu vào x và một đích tương ứng t, mục đích là tìm ra hàm f(x) thoả mãn tất cả các mẫu học đầu vào.

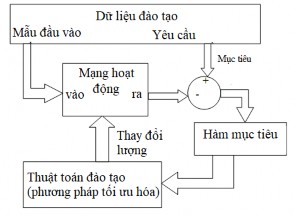
Hình 2.13. Mô hình học có thầy (Supervised learning model)

- Học không có thầy (Unsupervised Learning):

Với cách học không có thầy, không có phản hồi từ môi trường để chỉ ra rằng đầu ra của mạng là đúng. Mạng sẽ phải khám phá các đặc trưng, các điều chỉnh, các mối tương quan, hay các lớp trong dữ liệu vào một cách tự động. Trong thực tế, đối với phần lớn các biến thể của học không có thầy, các đích trùng với đầu vào. Nói một cách khác, học không có thầy luôn thực hiện một công việc tương tự như một mạng tự liên hợp, cô đọng thông tin từ dữ liệu vào.

2.5. Một số ứng dụng của mạng nơ-rôn

Mạng nơ-rôn được coi như một hộp đen biến đổi đầu vào m biến thành vec-tơ ra n

biến. Các biến của vec-tơ vào và ra có thể là các số thực, tốt nhất nằm trong khoảng [0, 1]

hoặc [-1, 1]; số nhị phân 0, 1 hay số nhị cực -1, +1. Số biến của vec-tơ vào/ra không bị hạn chế song sẽ ảnh hưởng tới thời gian tính và tài nguyên của máy tính. Với số lượng lớn các biến của các vec-tơ đầu vào và ra đồng nghĩa với việc tăng số lượng các số liệu quan sát. Thường số biến của vec-tơ ra nhỏ hơn số biến của vec-tơ vào nhưng không phải bắt buộc là như vậy. Các lĩnh vực mà mạng nơ-rôn thường được ứng dụng là:

- Phân loại (Classification)

- Mô hình hoá (Modeling)

- Biến đổi (Transformation and mapping)

a. Phân loại

Một trong các công việc đơn giản và thường được sử dụng nhiều trong việc quản lý các đối tượng đa biến là phân loại. Đó có thể là sắp xếp các đối tượng vào các tập theo từng loại hoặc theo tầng lớp hoặc theo các lớp con của các lớp lớn hơn.

Thường xuyên việc phân loại theo tầng lớp bao gồm nhiều mức của các tập ra quyết định, phân lớp một đối tượng vào nhúm, nhúm con, chủng loại, chủng loại con, hoặc lớp. Ví dụ trong hoá học việc dự báo các đặc điểm cấu trúc khác nhau cùng một hợp chất chưa biết trên phổ của nó.

b. Mô hình hoá

Các hệ thống phân loại đưa ra các câu trả lời rời rạc như có, không hoặc một số nguyên định danh đối tượng đầu vào thuộc lớp nào. Tuy nhiên, việc mô hình hoá yêu cầu hệ thống phải sản sinh ra các câu trả lời mang tính liên tục. Trong việc mô hình hoá một số lượng nhỏ các số liệu được sử dụng để xây dựng mô hình. Mô hình này có thể đưa ra các dự báo cho tất cả các đối tượng đầu vào có thể. Việc tìm ra đường cong phù hợp với các số liệu thực nghiệm (curve- fitting) là một trong những ứng dụng thuộc dạng này. Trong phần lớn các ứng dụng chúng chỉ là thủ tục một biến vào - một biến ra như sau:

Y = f(x, a, b, … , p) (2.8)

Ở đây hàm f chứa một tập các tham số a, b, …., p. Các tham số này phải được xác định bằng việc tối thiểu hoá độ chênh lệch giữa số liệu thực nghiệm và giá trị tính toán từ mô hình:

 (y thực nghiệm - ymô hình)2  min (2.9)

Mô hình hoá cũng có thể là vấn đề nhiều biến vào - một biến đầu ra hoặc nhiều biến đầu vào - nhiều biến đầu ra.

Trong bất kỳ loại mô hình nào thì cũng phải tuân theo một giả định là: các thay đổi nhỏ của tín hiệu đầu vào sẽ chỉ gây ra những biến đổi nhỏ của tín hiệu ra.

Trong các vấn đề đa biến mạng nơ-rôn có nhiều lợi thế hơn so với các phương pháp mô hình hoá cổ điển sử dụng các hàm giải tích, các phương pháp mô hình hoá cổ điển đối với mỗi biến đầu ra chúng ta phải khẳng định trước một hàm giải tích cùng một bộ các tham số trong khi đó đối với mạng nơ-rôn chúng ta không cần bất kỳ sự hiểu biết trước về các tham số đó.

c. Biến đổi

Việc biến đổi nhằm mục đích nộn các đối tượng từ không gian m chiều vào không gian có số chiều nhỏ hơn rất nhiều (2 hoặc 3). Qua việc nộn các đối tượng này sẽ bộc lộ các đặc điểm mà chúng ta không thể nhận thấy khi các đối tượng ở trong không gian nhiều chiều.

Những câu hỏi mà việc biến đổi có thể trả lời là: Bản đồ của toàn bộ các đối tượng như thế nào? Có bao nhiêu vùng trong bản đồ có thể phân biệt được? Hình dáng của các vùng đó như thế nào? Các đặc điểm của các đối tượng thể hiện qua các vùng bản đồ như thế nào?

2.6. Một số mạng nơ-rôn được đề xuất để ứng dụng nhận dạng tín hiệu điện tim

2.6.1. Mạng MLP

2.6.1.1. Cấu trúc mạng

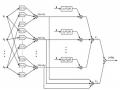
Mạng MLP là mạng nơ-rôn phổ biến nhất, nó là một mạng truyền thẳng với các phần tử cơ bản gọi là nơ-rôn [6]. Trong luận văn sử dụng mạng MLP với một lớp ẩn được trình bày trong hình 2.14. Nhiệm vụ đặt ra là phải xác định cấu trúc cố định cho mạng MLP: Số lớp ẩn, hàm truyền đạt của mỗi lớp, số lượng nơ-rôn trên mỗi lớp, trọng số ghép nối giữa nơ-rôn trong mô hình MLP có thể được điều chỉnh lại cho phù hợp trong quá trình học để xuất các tín hiệu đầu ra mong muốn. Thuật toán của quá trình học được sử dụng cho mô hình MLP trong luận văn này đã được đề xuất bởi Levenberg và Marquardt [6, 30].

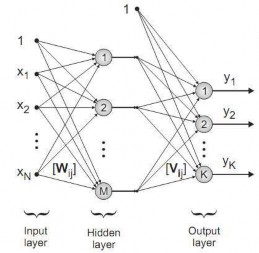
Hình 2.14. Mạng MLP với một lớp ẩn

Xem tất cả 98 trang.