Thuật Toán Học Theo Bước Giảm Cực Đại Cho Mạng Mlp

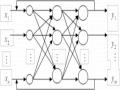
Theo [6] mạng MLP với một lớp ẩn có thể được đặc trưng bởi các thông số sau:

- Bộ ba (N, M, K ), trong đó N – số đầu vào, M – số nơ-rôn thuộc lớp ẩn, K – số nơ-rôn ở lớp đầu ra.

- Các hàm truyền đạt f1 của lớp ẩn và f2 của lớp đầu ra.

- Ma trận trọng số W kết nối giữa lớp đầu vào và lớp ẩn (Wij - trọng số ghép nối giữa nơ-rôn ẩn thứ i và đầu vào thứ j), ma trận các trọng số V kết nối giữa lớp ẩn và lớp đầu ra (Vij trọng số ghép nối giữa nơ-rôn đầu ra thứ i và nơ-rôn ẩn thứ j)

Khi đó, với véc-tơ đầu vào x x1, x2,...,xN(đầu vào phân cực cố định x0=1)

ta có đầu ra được xác định tuần tự theo chiều “lan truyền thuận” như sau:

(1) Tổng đầu vào của nơ-rôn ẩn thứ i (i=1,2,...,M):

Có thể bạn quan tâm!

• Tổng Quan Về Các Phương Pháp Nhận Dạng Tín Hiệu Điện Tim‌
• Định Hướng Nghiên Cứu Của Đề Tài
• Một Số Mạng Nơ-Rôn Được Đề Xuất Để Ứng Dụng Nhận Dạng Tín Hiệu Điện Tim
• Xây Dựng Mô Hình Phối Hợp Các Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim
• Phối Hợp Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim Bằng Mô Hình Cây Quyết Định
• Quy Trình Xây Dựng Cây Quyết Định Cho Khối Tổng Hợp Kết Quả

Xem toàn bộ 98 trang tài liệu này.

N

ui x j .Wij j 0

(2.10)

(2) Đầu ra của nơ-rôn ẩn thứ i (i=1, 2 ,..., M), đầu vào phân cực của các nơ-rôn lớp ra là v0  1.

vi 

f1ui

(2.11)

(3) Tổng đầu vào của nơ-rôn đầu ra thứ i (i=1, 2, ..., K):

M

gi v j.Vij j 0

(4) Đầu ra thứ i (i=1, 2, ..., K) của mạng sẽ bằng:

(2.12)

(2.13)

yi 

f2gi

Tổng hợp lại ta có hàm truyền đạt của mạng MLP là một hàm phi tuyến có công thức như sau:

yi 



f2gi

f2 

v j .Vij f2 

f1(u j).Vij

MM

j 0 j 0 

M N



f2 f1 xk .Wjk Vij 

j 0 

k 0



(2.14)

2.6.1.2. Thuật toán học theo bước giảm cực đại cho mạng MLP

Quá trình điều chỉnh các thông số của mạng để thích nghi với bộ số liệu được gọi là quá trình học của mạng MLP hay còn được gọi là quá trình huấn luyện (train) mạng MLP theo một bộ mẫu cho trước [6].

Trong số các thông số đã nêu ở trên, nếu như các thông số cấu trúc (số đầu vào, số đầu ra, số lớp ẩn, các hàm truyền đạt của mỗi lớp ẩn, số nơ–rôn trên mỗi lớp ẩn) thường được chọn bằng thực nhiệm hoặc bằng phương pháp thử với các giá trị rời rạc nhất định thì các thông số trọng số ghép nối giữa các nơ–rôn có thể được điều chỉnh thích nghi bằng các thuật toán tối ưu hóa (còn gọi là thuật toán “học”). Các thuật toán “học” của mạng nơ–rôn có các ý tưởng cũng hoàn toàn tương tự như các thuật toán học của nơ–rôn, tuy nhiên cần chú ý rằng mức độ phức tạp của công thức là cao hơn do cấu trúc mạng nơ–rôn phức tạp hơn so với từng nơ–rôn đơn lẻ.

Tương tự như đối với nơ–rôn đơn lẻ, các thuật toán thông dụng nhất để điều chỉnh thích nghi các trọng số của một mạng nơ–rôn là các thuật toán sử dụng gradient như thuật toán bước giảm cực đại, thuật toán Levenberg – Marquardt, …

Khi sử dụng thuật toán bước giảm cực đại, ta cũng khởi tạo các giá trị trọng số bằng các giá trị ngẫu nhiên nào đó: [w] = [w](0); [v] = [v](0). Sau đó ta sẽ xây dựng công thức lặp để điều chỉnh liên tiếp các giá trị này để hàm sai số tiến tới cực trị. Ta có các công thức thay đổi các trọng số trong hai ma trận W và V để xác định điểm cực trị của hàm mục tiêu E như sau:

W t 1W t E





W

E



V t 1V t 



V

(2.15)

với hàm mục tiêu E cho theo (2.9) và độ lệch giữa véc–tơ đầu ra yi của mạng MLP và véc–tơ giá trị đích di được tính theo các công thức tính khoảng cách như các công thức từ (2.10) đến (2.14).

Từ các công thức (2.10) đến (2.14) và (2.15) đã nêu trên ta có:

Ep K

yij

V ( yij dij ) V

(2.16)

Trong đó:

i1 j 1 

yij gij 

M Vjk

V f2gij V

f2 gij vik V

(2.17)

k 0 

Từ đó:

Nhưng

Vjk

V

 1 chỉ khi j 

và k 

, Vjk

V

 0 trong các trường hợp còn lại.

Một cách tương tự:

E

V

p



i1

yi

di

f2gi

vi

(2.18)

E

p K



y d

f g

V f u x

(2.19)

W



i1 j 1

ij ij 2 i

j1 i i

Với các công thức gradient này, ta có thể tiến hành điều chỉnh thích nghi các giá trị của hai ma trận W và V để tìm cực tiểu của hàm sai số.

Ta có các công thức để điều chỉnh thích nghi các trọng số của mạng MLP theo thuật toán Levenberg – Marquardt [5]:

W (t 1) 

W (t ) –

[H Wt ]1 gWt 

(2.20)

trong đó:

V (t 1) 

V (t ) –

[H Vt ]1 gVt 

(2.21)

, – các ma trận chứa các trọng số ghép nối và tại bước lặp thứ (t)

trong quá trình thích nghi;

vec – tơ gradient của hàm sai số theo từng trọng số trong các ma

trận;

ma trận gradient bậc hai của hàm sai số theo cặp trọng số từ các

ma trận W và V tương ứng;

2.6.2. Mạng nơ-rôn mờ TSK

2.6.2.1. Cấu trúc mạng

Để tái tạo lại các phương pháp tính toán của mô hình TSK, các tác giả Takagi, Sugeno và Kang đã xây dựng một mô hình tính toán dưới dạng tương tự như một mạng truyền thẳng với cấu trúc như trên hình 2.15. Để đơn giản hóa mô hình và các công thức, ta tạm xét mạng có một đầu ra [5, 6].

Về mặt cấu trúc, mạng TSK được xác định bởi ba thông số N, M, K  với N  số đầu vào (số thành phần của véc–tơ x), M số quy tắc suy luận, K  số đầu ra (đang tạm xét là 1) và mạng TSK là một mô hình gồm năm lớp. Lớp đầu tiên được gọi là lớp mờ hóa, sử dụng để tính toán các giá trị điều kiện mờ thành phần:

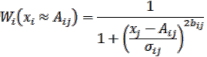(2.22)

Khi sử dụng hàm truyền đạt là hàm Gauss mở rộng, mỗi một khối sẽ có 3 véc – tơ thông số là Ai = [Ai1, Ai2, ..., AiN] – vec – tơ trọng tâm

của quy tắc, véc–tơ thông số độ rộng của quy tắc, bi = [bi1, bi2,

..., biN] - véc–tơ thông số hình dạng của quy tắc.

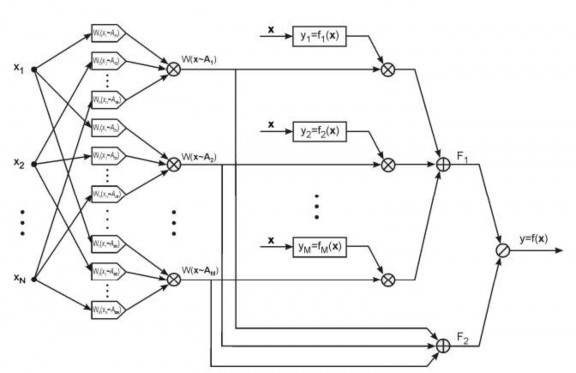
Hình 2.15. Mạng nơ–rôn mờ TSK

(1) Lớp thứ hai là lớp tính giá trị điều kiện lô–gic mờ tổng hợp cho toàn bộ

véc– tơ đầu vào W (x A) . Theo (2.22) ta có:

W (x A) = W1 (x1 A1). W2 (x2 A2). ... . WN (xN AN)

N

 1

2bi

(2.23)



i1 x A 

1i i



i 

nên lớp thứ hai này chỉ đơn giản là các khối nhân các tín hiệu đầu vào Wi (xi Ai) để tạo ra tín hiệu đầu ra tương ứng.

(2) Lớp thứ ba được sử dụng để tính toán giá trị các hàm TSK fi(x) (là các hàm tuyến tính qi0 +) và nhân với giá trị mờ của điều kiện lô–gic W (x Ai). Lớp này có chứa các thông số cần xác định là các hệ số qij (vớii  1, 2, , M – số luật của mạng và j  0,1, ..., N – số đầu vào của mạng) của các hàm tuyến tính TSK;

(3) Lớp thứ tư dùng để tính toán tổng các giá trị của lớp ba (F1) và lớp hai (F2) trong mạng để có được các thành phần tử số và mẫu số trong công thức (3.16);

(4) Lớp cuối cùng chỉ có duy nhất một khối chia để tính toán giá trị đầu ra của toàn mạng theo công thức:

FMWxA .y

y 1

i1 i i

(2.24)

FMWxA 

2

2.6.2.2. Thuật toán học cho mạng TSK

i1i

Cũng tương tự như đối với mạng MLP, mạng TSK học theo nguyên tắc “có hướng dẫn”, nghĩa là ứng với mỗi đầu vào ta sẽ có một giá trị đầu ra tương ứng từ mạng. Vì vậy, khi ta có một bộ số liệu gồm p mẫu xi, divới i  1, 2,..., p; xi  RN ; di

 RK , cần xây dựng một mạng TSK xấp xỉ bộ số liệu mẫu này sao cho:

i : yiTSK xidi

hoặc ta tìm cực tiểu của hàm sai số:

(2.25)

p

1 2 

(2.26)

2

E yidi

i1

min

Từ mô tả cấu trúc năm lớp của mạng TSK ở trên, ta thấy rằng mạng chỉ có hai lớp có chứa các thông số có thể điều chỉnh thích nghi theo bộ số liệu được, đó là lớp thứ nhất với các khối mờ hóa và lớp thứ ba với các hàm TSK tuyến tính. Các lớp thứ hai, thứ tư và thứ năm đều có cấu hình cố định, không phụ thuộc vào bộ số liệu.

Với mạng có N đầu vào, M quy tắc suy luận và K đầu ra, ta có số lượng thông số của các khối mờ hóa là 3MN (và đây là các thông số phi tuyến), số lượng các thông số của các hàm tuyến tính TSK là: M(N+ 1) K. Do đó ta có thể nhận thấy số lượng các tham số của mạng TSK là khá lớn. Việc tối ưu hóa hàm sai số (2.26) với số lượng lớn các tham số như vậy sẽ rất phức tạp, thời gian tính toán lâu và xác suất để quá trình hội tụ về một điểm cực tiểu tốt là thấp. Vì vậy một thuật toán hỗn hợp đã được đề xuất trong [24], theo đó ta tách quá trình chỉnh thích nghi thành hai quá trình con: Điều chỉnh các thông số tuyến tính và điều chỉnh các thông số phi tuyến. Thuật toán điều chỉnh chung được mô tả như sau:

(1) Khởi tạo các giá trị ban đầu của các thông số phi tuyến và tuyến tính;

(2) Giữ nguyên giá trị các thông số tuyến tính, sử dụng thuật toán (lặp) điều chỉnh các thông số phi tuyến (số bước lặp được lựa chọn trước, thường khoảng 5 tới 10 bước);

(3) Giữ nguyên các giá trị của các thông số phi tuyến, sử dụng thuật toán điều chỉnh các thông số tuyến tính. Kiểm tra hàm sai số mục tiêu, nếu kết quả đã đạt yêu cầu thì dừng quá trình học, ngược lại thì quay lại bước 2.

a) Thuật toán điều chỉnh các thông số phi tuyến

Theo [6], ta có thể sử dụng nhiều thuật toán tối ưu hóa khác nhau cũng như đối với mạng MLP. Thuật toán cơ bản nhất là thuật toán bước giảm cực đại sử dụng gradient bậc nhất. Phần tiếp theo đây ta sẽ trình bày về thuật toán bước giảm cực đại để điều chỉnh các thông số phi tuyến.

Với bộ số liệu gồm p mẫu với i = 1, 2, ..., p; (tạm xét với mạng có một đầu ra), khi cho véc–tơ đầu vào xi = [xi1, xi2, ..., xiN], ta có đầu ra từ mạng TSK được tuần tự tính như sau:

1. Tính các giá trị mờ thành phần:

W x A  1

cho k = 1, 2, ..., M; và j = 1,2, ..., N.

ki ij ij

x A

2bkj

1ij kj

kj 

2. Tính giá trị điều kiện toàn phần cho k  1, 2, , : M:

WkxiAkWk1 xi1 Ak1 .Wk2 xi2 Ak2 ..WkN xiNAkN 

N

 1

2bkj





j 1 x A 

1ij kj





3. Tính đáp ứng đầu ra theo các công thức:

kj 

Mx

A . f

x 

y k 1

i k k i

(2.27)

k 1

i k

i M

x A 

Sau khi có được p giá trị đầu ra, ta tính được giá trị hàm sai số mục tiêu là:

2

E 1

p

yd 2

(2.28)

i i i1

Khi đó, thuật toán bước giảm cực đại áp dụng vào để thực hiện tối thiểu hóa hàm sai số E sẽ điều chỉnh các thông số phi tuyến như sau:



At 1At 



t 1t 

E

A

E



(2.29)





bt 1bt E

b



Cho = 1, 2, ..., M; =1, 2, ..., N.

p

Ta có từ hàm sai số E = 1

2 có thể xác định các gradient tuần tự như

2

( yi

i1

di )

sau. Để rút gọn, ta ký hiệu

ki WkxiAklà giá trị điều kiện toàn phần của luật thứ k

ứng với mẫu đầu vào thứ i trong bộ số liệu đã cho. Với các hệ số trọng tâm ta có:

E 1 p y

( yi di )i

A



2 i1

A

M. f

x 

M

.

k 1

ki k i

M. f

x .

k 1

ki 



p A

k 1

ki k i 

A

(2.30)





yi di 

2

i1 

M

ki 

k 1 





Ta có:

M. f

x 

. f

x 

W

x A

. f

.x 

k 1

ki k i

i  i  i  i 

A



WxiAf

A

.xi

A

A

(2.31)

Do hệ số chỉ xuất hiện trong công thức tính .

Rút gọn công thức (2.27) ta có:

WxiAf

.x .

M 

. f

x.WxiA

i

k 1 ki

k 1

M

ki k i



E p 

A

A

E

yi di 

A M 2 A

i1 

ki 





k 1 



p 

f.xi.

M M

. f x W x A 

ki 

ki k i  i 

yi di

k 1

M

k 1 2

A 

i1 

ki 



k 1 

1

M

(2.32)





p 

yi

di 

kki .f.xifkxi

2

.WxiA



i1 

M

ki 

A



k 1 

Theo công thức (2.21) ta có

WxiAW1 xi1 A1 .W 2 xi2 A 2 .WN xiNAN 

WxiAWxiAN

A A

.Wj xij Aj 



j 1 j 

W x A  1

(2.33)

 i

x 2b

iA

1



Với hàm truyền đạt Gauss mở rộng:

W x A  1

 i

x 2b

iA

1



ta có đạo hàm của hàm truyền đạt theo các thông số trọng tâm Acủa luật là:

2b

W

W x

A 1W

x A

khi x A





x A

 j i

 i

i

(2.34)

0

A



i

khi x

iA

xiA



Đạo hàm của hàm truyền đạt theo thông số hình dạng bcủa luật là:



W 

2ln W x A 1W

x A khi x A





A

 i

 i

i

(2.35)

0





khi x

iA

và theo các thông số độ mở là:

W2bW x

A 1W

x A



(2.36)

A 

 i

i

Từ đó ta có:



WxiAWxiAN

A A

.Wj xij Aj 



2b

j 1 j 

N

x A

W1WWj xij Aj khi xiA





0

i

j 1 j 

khi x iA

2b

1W .W x A

khi x A

x A

 i 

i

(2.37)

i

0





khi x

iA