Xây Dựng Mô Hình Phối Hợp Các Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim

Sử dụng các công thức (2.30) và (2.32), ta có công thức tính gradient của hàm sai số E theo các trọng tâm của các hàm mờ hóa.

Tương tự như vậy chúng ta sẽ có các công thức cho gradient của hàm sai số E

theo các thông số độ mở và các thông số hình dạng b.

b) Thuật toán điều chỉnh thích nghi các thông số tuyến tính

Theo [6], để xác định các thông số tuyến tính, trước tiên ta biểu diễn hàm sai số E dưới dạng một hàm tuyến tính của các thông số này. Mạng TSK có các thông số tuyến tính là các hệ số qđược sử dụng trong các hàm f(xi ) , cụ thể:

N

fxiq 0 q1.xij.Với = 1, 2, ..., M; =1, 2, ..., N và K đầu ra ta có số

j 1

lượng thông số tuyến tính là M.(N+1).K. Các công thức sau đây được trình bày cho trường hợp mạng có một đầu ra (K=1).

Nếu đặt đầu vào phân cực ta có

N

fxiqj .xij

j 0

Biểu diễn tín hiệu đầu ra theo các thông số tuyến tính này ta có:

W x

M

A . f

x 

MWx

A .Nq.x

yk 1

k i k k i 

k 1

k i k

j 0

kj ij

iMWx

A 

MWx

A 

k 1



k i k

1

k 1

N M

k i k

1

M Wk xi Ak qkj .xij

kWkxiAkj0 k 1

1 N M

M qkjWk xi Ak xij

(2.38)

1

kWkxiAkj0 k 1

Từ đó ta có trong biểu diễn tín hiệu đầu ra ứng với tín hiệu đầu vào xi , thông số

qsẽ có hệ số tương ứng là:

xi yi 



WxiA.xi

k k i k1

MWxA 

(2.39)

Như vậy ứng với mỗi một mẫu tín hiệu đầu vào, ta có một phương trình yi  di cho M(N+1) ẩn số tuyến tính q.

Với bộ số liệu p mẫu, ta sẽ có hệ p phương trình tuyến tính cho M(N+1) ẩn. Bài

toán xác định các ẩn q

để tối ưu hóa hàm sai số

1 

2 có thể được giải

2

p

E

( yi

i1

di )

bằng nhiều phương pháp. Ví dụ ta có thể sử dụng phương pháp phân tích theo các hệ số kỳ dị (SVD – Singular Value Decomposition).

Sau khi đã tìm được các thông số tuyến tính mới, ta lại quay lại điều chỉnh các thông số phi tuyến theo thuật toán học đã lựa chọn (ví dụ như thuật toán bước giảm

cực đại như đã trình bày ở trên). Quá trình điều chỉnh này được thực hiện nhiều lần cho tới khi sai số giảm xuống dưới một mức  đã chọn trước hoặc ta đạt được số lần lặp tối đa cho trước

2.6.3. Máy véc-tơ hỗ trợ SVM

Máy vector hỗ trợ trong tiếng Anh là Support Vector Machine, viết tắt: SVM.

Máy vector hỗ trợ là một thuật toán giúp tìm ra một siêu phẳng phân cách tối ưu để có thể phân chia dữ liệu tuyến tính ra làm hai lớp khác nhau.

Máy vec-tơ hỗ trợ (SVM) là một trong những thuật toán phổ biến nhất trong học máy, được sử dụng để phân loại, hồi qui và phát hiện điểm dữ liệu bất thường.

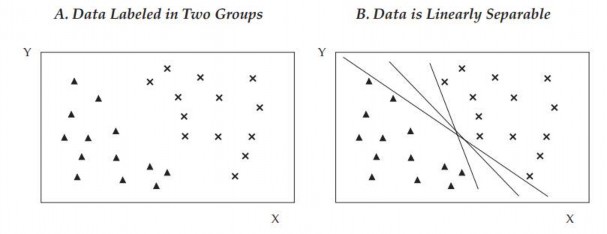
Hình 2.16. Vùng dữ liệu

Hình A (bên trái) trình bày một tập dữ liệu đơn giản với hai đặc tính (tọa độ x và y) được gán thành hai nhóm (hình tam giác và hình chữ thập) và tách thành hai vùng riêng biệt, có thể đại diện cho các cổ phiếu có lợi nhuận dương và âm trong một năm nhất định.

Hai vùng này có thể dễ dàng phân tách bằng nhiều đường thẳng; ba trong số chúng được hiển thị trong hình B (bên phải). Dữ liệu được phân tách tuyến tính và bất kỳ đường thẳng nào được hiển thị sẽ được gọi là phân loại tuyến tính - một phân loại nhị phân dựa trên sự kết hợp tuyến tính đặc trưng của từng điểm dữ liệu.

Ý tưởng đằng sau thuật toán SVM là tối đa hóa xác suất đưa ra dự đoán chính xác bằng cách xác định đường biên cách các quan sát xa nhất.

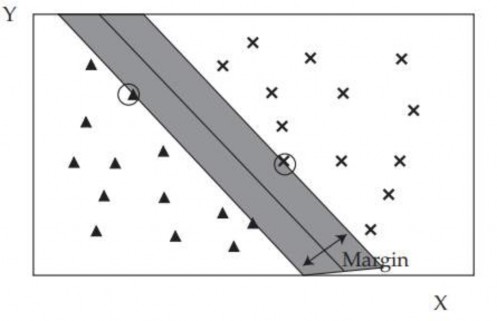
Hình 2.17. SVM phân tách dữ liệu bằng dải bóng mờ chia các quan sát thành hai nhóm. Đường thẳng ở giữa dải bóng mờ là đường biên (boundary).

* Ứng dụng

SVM có nhiều ứng dụng trong quản lý đầu tư. Nó đặc biệt phù hợp với các tập dữ liệu có qui mô từ nhỏ đến trung bình nhưng phức tạp, chẳng hạn như báo cáo tài chính doanh nghiệp hoặc cơ sở dữ liệu phá sản. Các nhà đầu tư tìm cách dự đoán các công ty hoạt động kém hiệu quả để xác định cổ phiếu để tránh đầu tư hoặc bán khống.

SVM có thể tạo ra một phân loại nhị phân (ví dụ: có khả năng phá sản so với khó có khả năng phá sản) bằng cách sử dụng nhiều biến số cơ bản và kĩ thuật. SVM có thể nhanh chóng nắm bắt các đặc điểm của dữ liệu đó với nhiều tính năng trong khi vẫn linh hoạt với các điểm dữ liệu bất thường và các đặc tính tương quan.

SVM cũng có thể được sử dụng để phân loại văn bản từ các tài liệu (ví dụ: tin tức, thông báo của các công ty và báo cáo thường niên của công ty) thành các nhóm hữu ích cho các nhà đầu tư (ví dụ: tâm lí tích cực và tâm lí tiêu cực).

2.6.4. Rừng ngẫu nhiên RF

Random Forest (rừng ngẫu nhiên) [10] là phương pháp học tập thể (ensemble) để phân loại, hồi quy được phát triển bởi Leo Breiman tại đại học California, Berkeley. Breiman cũng đồng thời là đồng tác giả của phương pháp CART [12].

Random Forest (RF) là phương pháp cải tiến của phương pháp tổng hợp bootstrap (bagging). RF sử dụng 2 bước ngẫu nhiên, một là ngẫu nhiên theo mẫu (sample) dùng phương pháp bootstrap có hoàn lại (with replacement), hai là lấy ngẫu nhiên một lượng thuộc tính từ tập thuộc tính ban đầu. Các tập dữ liệu con (sub-dataset) được tạo ra từ 2 lần ngẫu nhiên này có tính đa dạng cao, ít liên quan đến nhau, giúp

giảm lỗi phương sai (variance). Các cây CART được xây dựng từ tập các tập dữ liệu con này tạo thành rừng. Khi tổng hợp kết quả, RF dùng phương pháp bỏ phiếu (voting) cho bài toán phân loại và lấy giá trị trung bình (average) cho bài toán hồi quy. Việc kết hợp các mô hình CART này để cho kết quả cuối cùng nên RF được gọi là phương pháp học tập thể.

Đối với bài toán phân loại, cây CART sử dụng công thức Gini như là một hàm điều kiện để tính toán điểm tách nút của cây. Số lượng cây là không hạn chế, các cây trong RF được xây dựng với chiều cao tối đa.

Trong những năm gần đây, RF được sử dụng khá phổ biến bởi những điểm vượt trội của nó so với các thuật toán khác: xử lý được với dữ liệu có số lượng các thuộc tính lớn, có khả năng ước lượng được độ quan trọng của các thuộc tính, thường có độ chính xác cao trong phân loại (hoặc hồi quy), quá trình học nhanh.

Trong RF, mỗi cây chỉ chọn một tập nhỏ các thuộc tính trong quá trình xây dựng (bước ngẫu nhiên thứ 2), cơ chế này làm cho RF thực thi với tập dữ liệu có số lượng thuộc tính lớn trong thời gian chấp nhận được khi tính toán. Người dùng có thể đặt mặc định số lượng các thuộc tính để xây dựng cây trong rừng, thông thường giá trị mặc định tối ưu là √𝑝 cho bài toán phân loại và 𝑝⁄3 với các bài toán hồi quy (p là số lượng tất cả các thuộc tính của tập dữ liệu ban đầu). Số lượng các cây trong rừng cần được đặt đủ lớn để đảm bảo tất cả các thuộc tính đều được sử dụng một số lần. Thông thường là 500 cây cho bài toán phân loại, 1000 cây cho bài toán hồi quy. Do sử dụng phương pháp bootstrap lấy mẫu ngẫu nhiên có hoàn lại nên các tập dữ liệu con có khoảng 2/3 các mẫu không trùng nhau dùng để xây dựng cây, các mẫu ngày được gọi là in-bag. Khoảng 1/3 số mẫu còn lại gọi là out-of-bag, do không tham gia vào việc xây dựng cây nên RF dùng luôn các mẫu out-of-bag này để kiểm thử và tính toán độ quan trọng thuộc tính của các cây CART trong rừng.

2.7. Kết luận chương 2

Trong chương này đã trình bày tổng quan về mạng nơ-rôn và một số ứng dụng của nó. So với các phương pháp truyền thống thì mạng nơ-rôn có một khả năng vượt trội, tuy nhiên để ứng dụng nó thành công cũng cần nghiên cứu nhiều khía cạnh về đào tạo mạng nơ-rôn, như lựa chọn cấu trúc mạng nơ-rôn, thiết kế tập mẫu học (nếu sử dụng phương pháp học có giám sát), và sau quá trình học phải tạo ra mạng nơ-rôn có tính tổng quát cao để có thể đem ứng dụng thực tế được tốt.

Mạng nơ-rôn nhân tạo là hướng tiếp cận mới trong công tác nhận dạng và dự báo đã nhận được sự quan tâm đặc biệt của một số nhóm nghiên cứu trên thế giới. ANN được coi là công cụ mạnh để giải quyết các bài toán có tính phi tuyến, phức tạp.

Trên cơ sở nghiên cứu, tìm hiểu về mạng nơ-rôn và một số ứng dụng của nó. Chương tiếp theo là ứng dụng, phối hợp một số mạng nơ-rôn để nhận dạng tín hiệu điện tim nhằm nâng cao độ chính xác.

Chương 3. XÂY DỰNG MÔ HÌNH PHỐI HỢP CÁC MẠNG NƠ-RÔN NHẬN DẠNG TÍN HIỆU ĐIỆN TIM

Định hướng của luận văn là xây dựng giải pháp kết hợp nhiều mạng nơ-rôn nhằm tăng độ chính xác so với các mô hình nhận dạng đơn ban đầu. Luận văn sử dụng cây quyết định để thực hiện việc kết hợp này. Để kiểm nghiệm chất lượng của đề xuất, luận văn sử dụng kết quả các mô hình nhận dạng đơn MLP, TSK, SVM và RF để tạo ra các mô hình kết hợp khác nhau. Như đã trình bày ở trên, các mô hình đơn này được lựa chọn làm các mô hình nhận dạng cơ sở vì đây là các mô hình đã có các kết quả đã được công bố trên các tạp chí và hội thảo quốc tế nên đảm bảo được sự khách quan và tính chính xác, đồng thời cũng là những kết quả đươc thực hiện trên cùng một bộ số liệu đầu vào nên việc so sánh sẽ thuận tiện và có tính thuyết phục. Nội dung chính của chương 3 gồm:

- Đầu tiên, tác giả trình bày phương pháp trích chọn đặc tính tín hiệu điện tim ECG để phục vụ cho quá trình nhận dạng;

- Tiếp theo, tác giả trình bày ngắn gọn về mặt lý thuyết, quy trình xây dựng các mô hình nhận dạng đơn MLP, TSK, SVM và RF, vì những mô hình này khá kinh điển và đã được nhiều tài liệu khác trình bày rất đầy đủ;

- Tiếp nữa, trình bày về giải pháp nâng cao chất lượng (độ chính xác) nhận dạng tín hiệu điện tim ECG dựa trên việc sử dụng cây quyết định DT để kết hợp nhiều mô hình nhận dạng đơn.

3.1. Trích chọn đặc tính tín hiệu điện tim ECG

Trích chọn đặc tính là quá trình tìm các giá trị đặc trưng của tín hiệu đầu vào gốc, lượng thông tin của đặc tính tín hiệu tinh giản hơn nhiều so với tín hiệu gốc, nên khối lượng tính toán của khối nhận dạng sẽ giảm. Việc lựa chọn loại đặc tính thường dựa trên độ phân tách đối tượng của nó. Do đó, khâu phân tích và trích chọn đặc tính đóng vai trò quan trọng, cho phép hỗ trợ việc đưa ra kết quả nhận dạng được dễ dàng và chính xác hơn. Cụ thể thực hiện các công việc sau:

- Đầu tiên, phải lựa chọn giải pháp trích chọn đặc tính, trong luận văn lựa chọn sử dụng các hàm Hermite để phân tích các tín hiệu ECG, do sự phù hợp về hình dạng biến thiên tín hiệu của chúng đối với tín hiệu điện tim, và có chứa các thành phần tần số khác nhau nên phù hợp cho việc mô tả các thành phần biến thiên khác nhau của tín hiệu điện tim (chi tiết sẽ trình bày ở mục 3.1.2);

- Tiếp theo, cần khảo số lượng đặc tính, nếu sử dụng quá ít đặc tính sẽ khiến cho mô hình nhận dạng bị thiếu hụt thông tin nên kết quả không chính xác, nhưng nếu sử dụng quá nhiều đặc tính sẽ khiến cho mô hình trở nên cồng kềnh, khó huấn luyện (lựa chọn được các tham số tối ưu cho bộ số liệu mẫu) và còn có thể ảnh hưởng xấu đến kết quả nhận dạng. Do đó, quan trọng là lựa chọn được các đặc tính tốt, có độ phân tách

cao. Để khảo sát và đánh giá, có thể này sử dụng cây quyết định DT (Decision Tree) hay

phân tích thành phần chính PCA (Principle Component Analysis ) [3].

Giải pháp trích chọn đặc tính của luận văn thể hiện trong hình 2.4 sau đây:

x 

18

Trung bình của 10 khoảng cách R-R cuối cùng.

Phát hiện đỉnh R, tách QRS với độ dài 250ms

Phân tích QRS bằng 16 hàm Hermite cơ sở

Khoản cách 2 đỉnh R-R liên tiếp

x in

Hình 3.1. Sơ đồ quy trình xây dựng véc tơ đặc tính cho tín hiệu điện tim

3.1.1. Phát hiện đỉnh R

Phức bộ QRS trong tín hiệu điện tim ECG tuy không chứa toàn bộ các thông tin để đánh giá tín hiệu điện tim, nhưng cũng chứa đựng khá nhiều các thông tin hữu ích và được nhiều tác giả trong nước và quốc tế sử dụng. Do đó, như đã trình bày ở trên, luận văn sử dụng số liệu phân tích từ phức bộ QRS và hai giá trị thời gian là khoảng cách R-R, trung bình 10 khoảng cách R-R cuối cùng để làm cơ sở nhận dạng. Theo khảo sát, phức bộ QRS kéo dài khoảng 100ms, tuy nhiên trong trường hợp bệnh lý phức bộ này có thể kéo dài gấp vài lần. Vì vậy, luận văn lựa chọn độ dài 250ms xung quanh đỉnh R là đủ rộng để chứa toàn bộ đoạn QRS, nếu tần số lấy mẫu tín hiệu điện tim là 360Hz thì 250ms tương ứng với khoảng 91 giá trị xung quanh đỉnh R (ta lấy 45 giá trị liền trước đỉnh và 45 giá trị từ đỉnh về phía sau).

Trong luận văn, áp dụng thuật toán phát hiện đỉnh R đã được Pan và Tompkins đưa ra vào năm 1985 [17../../CONG TAC TRUONG/DE TAI NCKH/CAP

BO/2019/Tai lieu/1. LUAN AN (2018)_sau phan bien kin.docx - _ENREF_82] và được phát triển tiếp vào năm 1986 [22]. Năm 2002, tác giả đã thay đổi một vài thông số để làm tăng độ chính xác và giảm được thời gian tính toán, thích hợp với việc nhúng chương trình xuống vi xử lý thay vì chạy trên máy tính. Lưu đồ hoạt động của thuật toán được trình bày trong hình 2.2.

Lọc thông thấp

Lọc thông

cao

|d[ ]/dt|

Phát hiện đỉnh R

16 1∑ 16 1	z[n]

Có thể bạn quan tâm!

• Định Hướng Nghiên Cứu Của Đề Tài
• Một Số Mạng Nơ-Rôn Được Đề Xuất Để Ứng Dụng Nhận Dạng Tín Hiệu Điện Tim
• Thuật Toán Học Theo Bước Giảm Cực Đại Cho Mạng Mlp
• Phối Hợp Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim Bằng Mô Hình Cây Quyết Định
• Quy Trình Xây Dựng Cây Quyết Định Cho Khối Tổng Hợp Kết Quả
• Các Chỉ Tiêu Đánh Giá Chất Lượng Mô Hình Nhận Dạng Tín Hiệu Điện Tim

Xem toàn bộ 98 trang tài liệu này.

x[n] y[n]

Input Output

Hình 3.2. Sơ đồ hoạt động của thuật toán phát hiện đỉnh R

Tiếp theo, trình bày về các bước thực hiện thuật toán tách phức bộ QRS của Hamilton và Tompkins, đã được áp dụng trong luận văn.

Bước 1: Lọc số

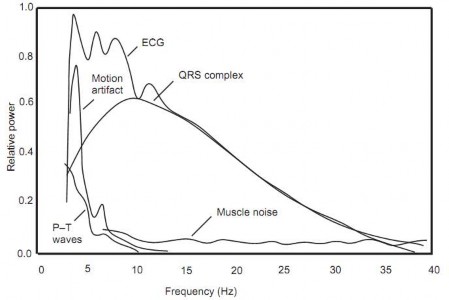
Hình 3.3. Phân bố phổ năng lượng của tín hiệu ECG

Theo [33] thì phức bộ QRS chủ yếu tập trung lân cận tần số 10Hz (như trên hình 3.3). Trong thuật toán phát hiện QRS của Hamilton và Tompkins đã sử dụng bộ lọc lấy dải trong khoảng tần số từ 5Hz đến 11Hz. Kết quả sau bộ lọc thông thấp 11Hz và thông cao 5Hz theo hình 3.4 đã không còn thành phần tần số thấp đặc trưng của sóng P, T hay trôi dạt đường cơ bản, hay thành phần tín hiệu gây ra bởi nhiễu điện lưới 50Hz và nhiễu có tần số cao. Hệ số của hai bộ lọc này đều là số nguyên bởi vì: điều này cho phép thực hiện cả ở trên các bộ vi xử lý để đáp ứng tốc độ xử lý nhanh theo thời gian thực. Hàm truyền của hai bộ lọc thông thấp và thông cao, được thực hiện trên phần mềm Matlab, kết quả như sau:

- Hàm truyền của bộ lọc thông thấp, với tần số cắt là 11Hz:

yn 2yn 1yn  2xn 2xn  5xn 10

Hàm truyền của bộ lọc thông cao, với tần số cắt là 5Hz:

y ny n 1xnxn 32

(3.1)

(3.2)

Nhiễu

60Hz

Nhiễu tần số cao

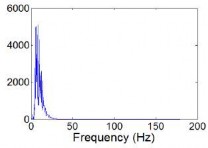
(a) (b)

Hình 3.4. Phân bố phổ năng lượng của tín hiệu ECG gốc (a), kết quả sau khi lọc (b)

Bước 2: Xác định cửa sổ thời gian có chứa đỉnh R

Theo thuật toán xác định R như hình 3.6 thì sau khi bước loại bỏ nhiễu bên ngoài khoảng 5÷11Hz. Kết quả sau bộ lọc nhiễu sẽ được xử lý tiếp qua các bước như sau:

- Lấy đạo hàm (d[ ]/dt): Tín hiệu điện tim ECG qua khâu xử lý này sẽ làm nổi thêm phức bộ QRS, ngoài ra đạo hàm còn loại bỏ tiếp các sóng nhỏ và thành phần biến thiên chậm như sóng T, P trong sóng ECG. Hình dạng của sóng ECG sau bước này gần như chỉ còn các phức bộ QRS, nhiễu đã bị loại bỏ, thể hiện trong hình 3.6-c.

y n 2xn

+ x n 1x n  3 2x n 4

(3.3)

- Lấy trị tuyệt đối: Để không triệt tiêu thông tin khi sử dụng phép toán lấy trung bình ở bước kế tiếp thì phải làm dương giá trị. Năm 1986, Hamilton và Tompkins [22] làm dương giá trị bằng phép toán bình phương, cách bình phương này có thêm tác dụng làm nổi bật những giá trị có biên độ cao như đỉnh R. Đến năm 2002

[23] tác giá đã thay bằng phép lấy trị tuyệt đối, nó có ưu điểm làm giảm bớt thời gian tính toán mà vẫn đạt được mục đích. Kết quả thể hiện trong hình 3.6-d.

yn

xn

(3.4)

+x n

- Lấy trung bình tín hiệu theo thời gian: Mục đích bước này là nhập các đỉnh gần nhau lại thành một dạng liền nhau giống như trong hình 3.6-e, sử dụng kết quả của bước này để tìm cửa sổ thời gian có chứa đỉnh R. Kết quả sau bước lấy trung bình tín hiệu theo thời gian thể hiện trong hình 3.6-e.

yn

1 xn 15+ xn 14+



16

(3.5)

- Xác định cửa sổ thời gian có chứa đỉnh R: Dựa vào kết quả đầu ra của bước

lấy trung bình tín hiệu theo thời gian

zn(theo hình 3.2) để xác định sơ bộ thời điểm

và khoảng thời gian có chứa đỉnh R. Từ đó, tham chiếu trở lại tín hiệu ECG sau lọc yn(theo hình 3.2) trong khoảng thời gian đó áp dụng thuật toán tìm Max để xác định đỉnh R. Trong hình 3.5 thể hiện mối quan hệ lý tưởng giữa phức bộ QRS với tín hiệu

lấy trung bình theo thời gian

zn. Đỉnh R sẽ xuất hiện ở khoảng giữa sườn lên của

xung trong tín hiệu

zn. Từ thực nghiệm Hamilton và Tompkins lấy độ rộng của cửa

sổ từ 150 đến 250 ms.

M

(a)

(b)

Hình 3.5. Mối quan hệ giữa QRS (a) và tín hiệu lấy trung bình tín hiệu theo thời gian (b)