ECG data
Tiền xử lý
quả cao đối với các bài toán sử dụng nhiều mô hình nhận dạng đơn và cùng một thuật toán, do đó khối lượng tính toán lớn nên ở khâu kết hợp các tác giả thường lựu chọn các giải pháp kết hợp đơn giản, hay dùng nhất là giải pháp biểu quyết theo đa số.
Trích chọn đặc tính
Vector đặc tính: x= [c0, ..., c15, RRlast, Rmean
Mô hình nhận dạng C1 có kết quả:
Y1 = [y11y12...y1K]
Mô hình nhận dạng C2 có kết quả:
Y2 = [y21y22...y2K]
Mô hình nhận dạng CM có kết quả:
YM = [yM1yM2...yMK]
Ghép thành vector tổng Y
Y = [y1 y2 ... yM] = [y11 y12 ... y1K y21y22 ... yM1yM2...yMK]
Khối kết hợp kết quả bằng cây quyết định DT
Kết quả nhận dạng Z
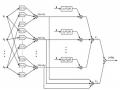
Hình 3.14. Sơ đồ khối chung của hệ thống kết hợp song song nhiều mô hình đơn
Luận văn đề xuất sử dụng cây quyết định DT (Decision Tree). Như đã trình bày ở trên, lựa chọn cây quyết định DT là để cân bằng với sự phức tạp của mô hình kết hơp, bởi vì các mô hình nhận dạng phi tuyến cơ sở đã phức tạp do đó khối kết hợp kết quả nên là một mô hình đơn giản hơn. Cây quyết định DT là một mô hình kinh điển dùng để phân loại dữ liệu [34], tuy nó đơn giản hơn mạng nơ-rôn trí tuệ tạo nhưng vẫn có thể thực hiện việc so sánh từng bước phức tạp và có những phương pháp hiệu quả trong việc hình thành các thông số của cây phỏng theo những tập dữ liệu được cho. Dưới sự đa dạng của các mô hình cây quyết định, tác giả sẽ lựa chọn dùng mô hình cây quyết định nhị phân (Binary Decision Tree) để tích hợp. Các kết quả tính toán mô phỏng sẽ được kiểm chứng trên các tập số liệu mẫu chuẩn của bộ CSDL MIT-BIH và MGH/MF được các nhóm nghiên cứu quốc tế thường dùng để tham chiếu, để đánh giả kết quả nhận dạng với các mô hình nhân dạng đơn, và với các giải pháp kết hợp. Luận văn sử dụng thuật toán ID3 [35] để xây dựng cấu trúc cho cây quyết định DT, chi tiết sẽ được trình bày trong các mục kế tiếp.
3.3.2. Quy trình xây dựng cây quyết định cho khối tổng hợp kết quả
Quy trình xây dựng khối tổng hợp kết quả bằng cây quyết định DT (trong hình 3.14), như sau:
Bước 1: Phân chia bộ dữ liệu gốc thành hai phần:
- Bộ dữ liệu học xlearn, d learncó P mẫu;
- Bộ dữ liệu kiểm tra xtest , dtestcó Q mẫu.
Bước 2: Xây dựng các mô hình nhận dạng cơ sở Ci (với i=1, 2,…, M).
Bước 3: Thiết lập bộ số liệu học cho cây quyết định DT, cụ thể:
- Đưa P mẫu xlearn, d learn vào M mô hình nhận dạng cơ sở Ci (đã xây dựng ở bước 2) thì sẽ có M kết quả nhận dạng yi = [yi1yi2...yiK] (i=1, 2,…,M), K số lớp nhận dạng;
- Sắp xếp M kết quả Yi thành một véc-tơ đầu vào tổng Ylearn có kích thước
M xK , chi tiết sắp xếp:
Ylearn = [y1 y2 ... yM]
= [y11 y12 ... y1K y21y22 ... y2K ... yM1 yM2...yMK]
Như vậy bộ số liệu học cho cây quyết định DT là (Ylearn, dlearn).
Bước 4: Xây dựng cây quyết định cho khối tổng hợp kết quả từ bộ số liệu học
Ylearn , dlearn , luận văn sử dụng thuật toán ID3 để xây dựng cấu trúc cho cây quyết định DT, chi tiết sẽ được trình bày ở mục kế tiếp.
Bước 5: Áp các kết quả của bước 2 (các mô hình đơn), bước 4 (cây quyết định) để hoàn thành hệ thống nhận dạng có cấu trúc như trong hình 3.14. Kiểm tra sai số nhận dạng với bộ dữ liệu kiểm tra xtest ,dtest , đánh giá chất lượng mô hình.
Bộ số liệu học Ylearn , dlearn
Thuật toán
ID3
Cây quyết đinh
Hình 3.15. Sơ đồ nguyên lý quá trình tạo cây quyết định
3.3.3. Cây quyết định
Cây quyết định là một mô hình xử lý tín hiệu kinh điển đã được sử dụng rất rộng rãi trong nhiều ứng dụng thực tế. Cây là một đồ thị không có chu trình. Đồ thị G được định nghĩa chung bởi hai tập hợp G = (V, E), trong đó V là tập hợp các nút (vertex) còn E là tập hợp các cạnh (edge) nối hai nút của tập V. Đối với các cây, ta sử dụng trường hợp cạnh có hướng. Khi đó nếu đồ thị G không có chu trình kín thì được gọi là cây. Với mỗi cây ta có [3]:
- Tồn tại một nút được gọi là nút gốc;
- Các nút được nối với nhau bởi các nhánh có hướng còn gọi là cành. Với mỗi cành, nút gốc được gọi nút cha/mẹ, nút ngọn là nút con;
Mỗi nút trong cây có thể có từ một đến nhiều nút con. Các nút không có nút con còn được gọi là (nút) lá/ngọn của cây.
Cây quyết định là một trường hợp đặc biệt của cây, khi được thiết kế với mỗi nút sẽ có một điều kiện phân nhánh. Tại các nút lá sẽ có một giá trị tương ứng với kết quả nhận dạng. Trên hình 3.15 là mô hình của một cây quyết định đơn giản.
Trong các phương pháp xây dựng cây quyết định ta thường sử dụng cây nhị phân (bậc hai) để đơn giản hóa việc mô tả các thuật toán. Giả thiết này không làm giảm tính tổng quát của cây do một cây bậc bất kỳ đều có thể chuyển về một cây nhị phân tương đương. Hình 3.16 minh họa phương pháp chuyển một nút bậc 3 về thành 2 nút bậc hai trong một cây. Đồng thời các điều kiện phân nhánh tại mỗi nút ta sẽ sử dụng các điều kiện đơn (ở dạng x op A với op là toán tử so sánh cơ bản , , , , , )
Đối tượng nhận dạng
Điều kiện
phân chia
Điều kiện phân
chia/KQ nhận
Điều kiện phân chia/KQ nhận
Hình 3.16. Mô hình cây quyết định dạng nhị phân [3]
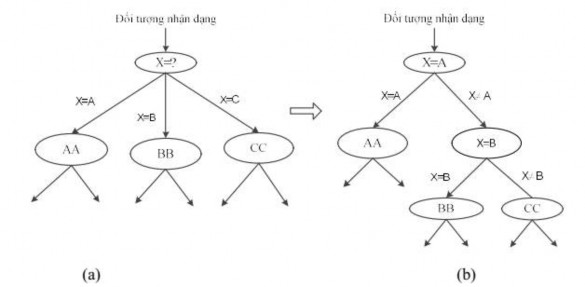
Hình 3.17. Chuyển một nút bậc cao (a) thành một nút nhị phân (b) [3]
Để xây dựng một cây quyết định cho một bộ mẫu số liệu cho trước, ta có thể sử dụng nhiều phương pháp khác nhau, trong đó phương pháp phổ biến nhất là ID3.
2
i
Nội dung cơ bản của phương pháp này dựa trên công thức lượng thay đổi entropy của một nút cây. Theo đó, với một bộ số liệu cho trước, nếu như tại một nút V ta có N số liệu x1, x2,..., xN thuộc M nhóm C1, C2,..., CM thì entropy của nút này sẽ là:
E(V) =
Mp log ( p )
(3.19)
i1
với pi= là xác suất số liệu 
của các nút thuộc về nhóm Ci. Với định nghĩa trên ta sẽ tiếp tục định nghĩa độ giảm entropy của nút khi sử dụng một điều kiện phân nhánh S này đó. Với nút V, khi sử dụng điều kiện phân nhánh S thì các số liệu được phân chia về các nút con SVi với số lượng là Ni 
Sử dụng công thức entropy cho từng nút, ta có độ giảm entropy của V khi sử dụng điều kiện S là:
Gain(V,S) = E(V) -
Ni E(SV )
i
(3.20)
i N
Đối với nút tất cả các điều kiện phân nhánh có thể sẽ được xem xét và kiểm tra (với một biến x có K giá trị khác nhau ta có thể tạo được K+1 điều kiện so sánh đơn để phân chia khác nhau). Điều kiện phân nhánh được lựa chọn sẽ là điều kiện phân nhánh ứng với độ giảm entropy lớn nhất. Quá trình phân nhánh sẽ được dừng lại khi tại mỗi nút lá tất cả các mẫu số liệu đều thuộc về cùng một nhóm.
Ví dụ 1: Xây dựng mô hình nhận dạng bằng cây quyết định
Xây dựng cây quyết định theo các bộ số liệu điện tâm đồ từ cơ sở dữ liệu MGH/MF. trong bảng 3.1 bộ số liệu học có 90 mẫu với ba nhóm bệnh là bình thường - N (30 nhịp, mã nhóm là 1), loạn nhịp trên thất - S (30 nhịp, mã nhóm là 2) và ngoại tâm thu thất - V (30 nhịp, mã nhóm là 3), bộ kiểm tra có 18 mẫu. Lựa chọn
véc-tơ đặc tính với 11 thành phần (10 giá trị đầu khai triển theo các hàm Hermite, giá trị cuối là khoảng cách R-R). Từ các véc-tơ đặc tính này, ta xây dựng cây quyết định nhị phân theo thuật toán ID3 và thu được kết quả được thể hiện trên hình 3.18.
Bảng 3.1. Bảng phân chia số lượng mẫu học và mẫu kiểm tra của 3 loại nhịp
Số mẫu học | Số mẫu kiểm tra | |
N | 30 | 6 |
S | 30 | 6 |
V | 30 | 6 |
Tổng | 90 | 18 |
Có thể bạn quan tâm!
-
Thuật Toán Học Theo Bước Giảm Cực Đại Cho Mạng Mlp -
Xây Dựng Mô Hình Phối Hợp Các Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim -
Phối Hợp Mạng Nơ-Rôn Nhận Dạng Tín Hiệu Điện Tim Bằng Mô Hình Cây Quyết Định -
Các Chỉ Tiêu Đánh Giá Chất Lượng Mô Hình Nhận Dạng Tín Hiệu Điện Tim -
Xây dựng mô hình phối hợp các mạng Nơ-rôn nhận dạng tín hiệu điện tim (ECG) - 11 -
Xây dựng mô hình phối hợp các mạng Nơ-rôn nhận dạng tín hiệu điện tim (ECG) - 12
Xem toàn bộ 98 trang tài liệu này.
Ví dụ số liệu cụ thể của sáu mẫu học (từ 
6) và ba mẫu kiểm tra (từ 
9)
x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | d | |
1 | -409.8 | 89.2 | -28.6 | -12.7 | -19 | -31.7 | -35.5 | -15.3 | -19.6 | -8.9 | 215.1 | 1 |
2 | -426.4 | 111.2 | -12.5 | -23.4 | 0 | -41.1 | -11.2 | -18.8 | -1.5 | -16.9 | 214 | 1 |
3 | -377.6 | 91.8 | 6.1 | -30 | -24.4 | -50.1 | -23.1 | -22.8 | -12.8 | -23.2 | 229.5 | 2 |
4 | -340.1 | 68.1 | 9.9 | -24.4 | -21.8 | -53.1 | -28.8 | -26 | -14.9 | -19.7 | 228.4 | 2 |
5 | 8.2 | -119.2 | -37.6 | -63 | -11.6 | -38.6 | -20.4 | -20 | -4.7 | -29.2 | 209 | 3 |
6 | -122.3 | 123.3 | -129.1 | 100 | -83.2 | 56.1 | -76.2 | 45.5 | -47.3 | 22.2 | 206.2 | 3 |
7 | -398.6 | 121.0 | -40.5 | -27.3 | 6.7 | -54.6 | -1.3 | -28.3 | 5.3 | -24.8 | 214.7 | ? |
8 | -365.8 | 76.7 | 17.7 | -30.7 | -21.6 | -47.7 | -29.6 | -25.3 | -18.1 | -21.2 | 221.6 | ? |
9 | 32.8 | -202.9 | -2.4 | -131.8 | 4.3 | -80.1 | 7.8 | -37.8 | 21.0 | -26.6 | 209.1 | ? |
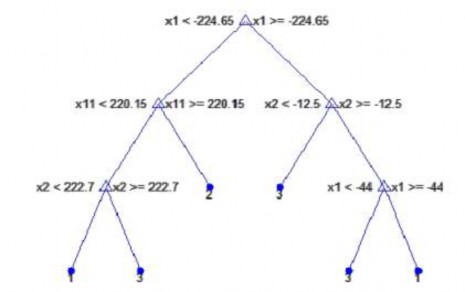
Hình 3.18. Cây quyết định xây dựng từ bộ số liệu có 90 mẫu (ví dụ 1)
Kết quả của cây nhị phân phân loại trọn vẹn ba loại nhịp bệnh được biểu diễn như trên hình 3.18 với chiều cao là bốn, có sáu lá. Các luật phân loại như sau:
Bảng 3.3 là kết quả thử nghiệm nhận dạng 18 mẫu mới, ta thấy chỉ có một mẫu bị nhận dạng nhầm từ S thành V.
Bảng 3.3. Ma trận phân bố kết quả nhận dạng ba loại mẫu nhịp bằng cây quyết định
N | V | S | |
N | 6 | 0 | 0 |
V | 0 | 6 | 1 |
S | 0 | 0 | 5 |
Tổng sai số | 0 | 0 | 1 |
Ví dụ 2: Tổng hợp kết quả bằng cây quyết định từ ba mô hình nhận dạng cơ sở: MLP, SVM, TSK, thử nghiệm với các mẫu số liệu lấy từ bộ cơ sở dữ liệu MGH/MF trong bảng 3.4.
Bảng 3.4. Bảng phân chia số lượng mẫu học và mẫu kiểm tra của 3 loại nhịp
Số mẫu học | Số mẫu kiểm tra | |
N | 8 | 2 |
S | 8 | 2 |
V | 8 | 2 |
Tổng | 24 | 6 |
Thực hiện theo quy trình đã trình bày ở mục trên (3.3.1. Xây dựng mô hình kết hợp), cụ thể:
- Kết quả nhận dạng của ba mô hình đơn MLP là y1, TSK là y2, SVM là y3;
- Số mô hình M=3, số lớp K=3, số mẫu dùng để học là 28 (theo bảng 3.4), nên
kết quả của mô hình nhận dạng đơn có dạng: yi = [yi1 yi2... yi3]
- Véc-tơ tổng có kích thước là 9 (M x K), thể hiện trong bảng 3.5: Số mẫu học là từ dòng 1-24, số mẫu kiểm tra từ dòng 25-30.
Ylearn = [y1 y2 y3] = [y11 y12 y13 y21 y22 y23 y31 y32 y33]
- Như vậy, bộ số liệu học cho cây quyết định DT là (Ylearn, dlearn) - dlearn là các mã loại nhịp tim đã biết trước, trong bảng 3.5 là dòng cuối cùng (Type d) có các mã (1- Loại nhịp bình thường N, 2- Loạn nhịp trên thất S, 3- Ngoại tâm thu thất S);
- Từ bộ số liệu trên ta tiến hành xây dựng cấu trúc cây quyết định, kết quả thể hiện trong hình 3.19.
Bảng 3.5. Bảng số liệu học và kiểm tra cho ví dụ 2
Véc-tơ tổng Y có kích thước (1x3*3) | Type d | |||||||||
y1 | y2 | y3 | ||||||||
y11 | y12 | y13 | y21 | y22 | y23 | y31 | y31 | y32 | ||
1 | 0.624 | 0.087 | 0.290 | 0.378 | -0.053 | 0.901 | 0.579 | 0.210 | 0.211 | 1 |
2 | 0.612 | 0.151 | 0.237 | 0.439 | 0.031 | 0.682 | 0.581 | 0.210 | 0.209 | 1 |
3 | 0.432 | 0.502 | 0.067 | 0.610 | 0.210 | 0.123 | 0.775 | 0.178 | 0.047 | 1 |
4 | 1.083 | 0.081 | -0.165 | 0.556 | 0.470 | 0.083 | 0.462 | 0.493 | 0.045 | 1 |
5 | 0.468 | 0.512 | 0.019 | 0.542 | 0.510 | -0.130 | 0.400 | 0.565 | 0.035 | 1 |
6 | 0.082 | 0.877 | 0.042 | 0.264 | 0.697 | -0.158 | 0.471 | 0.454 | 0.075 | 1 |
7 | 0.857 | 0.029 | 0.114 | 0.205 | -0.181 | 0.337 | 0.936 | 0.032 | 0.032 | 1 |
8 | 0.587 | -0.319 | 0.731 | 0.759 | -0.090 | 0.378 | 0.707 | 0.112 | 0.181 | 1 |
9 | 0.205 | 0.723 | 0.072 | 0.426 | 0.619 | -0.067 | 0.716 | 0.214 | 0.070 | 2 |
10 | 0.353 | 0.723 | -0.076 | 0.095 | 1.085 | -0.097 | 0.578 | 0.387 | 0.035 | 2 |
11 | -0.006 | 0.952 | 0.053 | 0.260 | 0.836 | -0.068 | 0.633 | 0.326 | 0.041 | 2 |
12 | 0.140 | 0.774 | 0.086 | 0.451 | 0.553 | -0.073 | 0.684 | 0.249 | 0.066 | 2 |
13 | 0.104 | 0.855 | 0.040 | 0.409 | 0.180 | -0.086 | 0.278 | 0.621 | 0.101 | 2 |
14 | -0.077 | 1.385 | -0.308 | 0.363 | 0.238 | 0.163 | 0.106 | 0.841 | 0.053 | 2 |
15 | -0.197 | 0.839 | 0.358 | -0.067 | 0.372 | 0.509 | 0.180 | 0.639 | 0.181 | 2 |
16 | 0.170 | 0.768 | 0.062 | 0.419 | 0.345 | 0.485 | 0.295 | 0.535 | 0.170 | 2 |
17 | 0.218 | 0.416 | 0.366 | -0.013 | 0.098 | 0.975 | 0.096 | 0.102 | 0.802 | 3 |
18 | 0.457 | 0.136 | 0.407 | 0.016 | 0.191 | 1.187 | 0.083 | 0.088 | 0.829 | 3 |
19 | 0.194 | 0.399 | 0.407 | 0.364 | 0.221 | 0.316 | 0.218 | 0.194 | 0.588 | 3 |
20 | 0.035 | 0.110 | 0.854 | 0.163 | 0.190 | 0.145 | 0.210 | 0.221 | 0.568 | 3 |
21 | 0.181 | -0.128 | 0.947 | 0.422 | 0.160 | 0.045 | 0.293 | 0.191 | 0.516 | 3 |
22 | 0.076 | 0.123 | 0.801 | 0.451 | 0.265 | 0.030 | 0.269 | 0.214 | 0.517 | 3 |
23 | 0.208 | 0.162 | 0.631 | 0.634 | 0.174 | 0.177 | 0.401 | 0.170 | 0.430 | 3 |
Véc-tơ tổng Y có kích thước (1x3*3) | Type d | |||||||||
y1 | y2 | y3 | ||||||||
y11 | y12 | y13 | y21 | y22 | y23 | y31 | y31 | y32 | ||
24 | -0.272 | 0.301 | 0.972 | 0.210 | 0.136 | 0.145 | 0.088 | 0.073 | 0.839 | 3 |
25 | 0.952 | -0.023 | 0.072 | 0.143 | 0.260 | 0.600 | 0.677 | 0.115 | 0.208 | ? |
26 | 0.674 | -0.097 | 0.424 | 0.085 | 0.287 | 0.293 | 0.544 | 0.254 | 0.202 | ? |
27 | 0.157 | 0.746 | 0.096 | -0.007 | 0.431 | 0.445 | 0.212 | 0.574 | 0.214 | ? |
28 | -0.101 | 0.655 | 0.447 | 0.178 | 0.221 | 0.656 | 0.242 | 0.554 | 0.203 | ? |
29 | 0.076 | 0.286 | 0.638 | 0.234 | 0.437 | 0.086 | 0.109 | 0.162 | 0.730 | ? |
30 | 0.236 | 0.204 | 0.560 | 0.271 | 0.366 | 0.351 | 0.324 | 0.181 | 0.495 | ? |
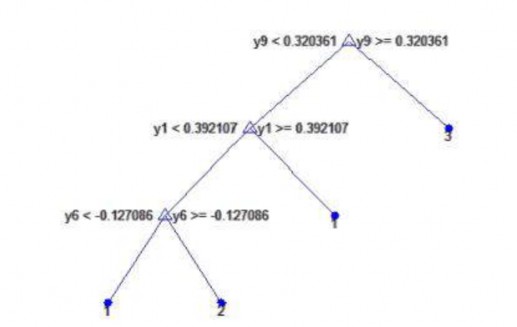
Hình 3.19. Cấu trúc cây quyết định tạo ra từ bộ số liệu trong bảng 3.5
Trong bảng 3.6 là kết quả nhận dạng với sáu mẫu mới (từ dòng 25-30 trong
bảng 3.5).