Về một phương pháp mới điều khiển mượn, khóa kênh tần số mạng di động tế bào - 11

sau:

Từ đó các tập mờ thành phần với các giá trị tâm ci và độ trải σi thu được như

0

 ( x1 c0 )2

AC (x ; c ,

) e

22

(3.3)

VC 1 0 0

1

 ( x1 c1 )2

AC (x ; c ,) e

22

(3.4)

C 1 1 1

2

 ( x1 c2 )2

AC (x ; c ,

) e

22

(3.5)

M 1 2 2

3

 ( x1 c3 )2

AC (x ; c ,

) e

22

(3.6)

H 1 3 3

4

 ( x1 c4 )2

AC (x ; c ,

) e

22

(3.7)

VH 1 4 4

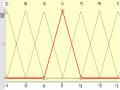
co c1 c2 c3 c4 Hình 3.3: Mờ hoá tín hiệu kênh cho phép AC

với x1 là tín hiệu đầu vào AC. Tương tự với tín hiệu TL thuộc khoảng [bmin, bmax ] và được mờ hoá thành các tập mờ Low (LL), Mederate (ML), Heigh (HL) (hình 3.4). Hàm liên thuộc mờ của các tập mờ này được xác định như sau:

(x b )2 / 22

i

(B j ) e

bj i bi

(3.8)

Với

b b , b , b , B j

là giá trị hàm liên thuộc tập mờ i tương ứng giá trị đầu vào xbj,

i 0 1 2 i

Bi LL, LM , LH. Sử dụng thuật phân vùng đều hoặc phân nhóm FCM đối với tập dữ

liệu huấn luyện đầu vào là tải lưu lượng TL thì các tâm bi và độ lệch bi

của hàm liên

thuộc dạng Gauss được xác định. Hàm liên thuộc của các tập mờ tương ứng với đầu vào tải lưu lượng được xác định cụ thể như sau:

( x2 b0 )2

TL (x ;b ,

) e b 0

(3.9)

2

2

LL 2 0 b 0

TL (x ;b ,

) e

( x2 b1 )2

2

2

b1

(3.10)

ML 2 1 b1

TL (x ;b ,

) e

( x2 b2 )2

2

2

b 2

(3.11)

HL 2 2 b 2

với x2 là tín hiệu đầu vào TL

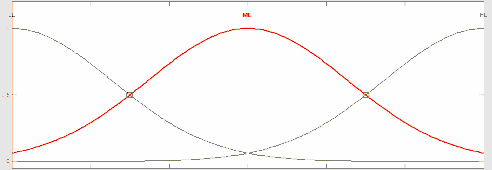
bo b1 b2 Hình 3.4: Mờ hoá tính hiệu tải lưu lượng TL

Khối giải mờ

Khối giải mờ dùng phương pháp trọng tâm cho phép ánh xạ giá trị biến ngôn ngữ đầu ra bộ điều khiển mờ thành giá trị điều khiển. Tín hiệu đầu ra là số kênh cho phép mượn cũng được xác định trong khoảng [-d, d]. Nếu qui ước số kênh mà tế bào cho phép các tế bào lân cận mượn là khoảng [-d,0] và số kênh mà tế bào hiện thời cần mượn từ các tế bào lân cận là khoảng [0,+d] thì khối giải mờ sẽ thực hiện ánh xạ giá trị mờ đầu ra vào khoảng giá trị [-d, d]. Trong bộ điều khiển này luận án định nghĩa các tập mờ đầu ra thành phần là các giá trị ngôn ngữ sau:

Bảng 3.1. Bảng định nghĩa giá trị biến ngôn ngữ

STT

Giá trị biến ngôn ngữ	Mô tả
1	NVL	Âm rất nhiều
2	NL	Âm nhiều (Nagative Large)
3	NM	Âm trung bình (Nagative Medium)
4	NS	Âm nhỏ (Nagative Small)
5	AZ	Xấp xỉ zero (Approximately Zero)
6	PS	Dương nhỏ (Positive Small)
7	PM	Dương trung bình (Positive Medium)
8	PL	Dương lớn (Positive Large)
9	PVL	Dương rất lớn (Positive Very Large)

Có thể bạn quan tâm!

• Pha Thỏa Thuận Với Tế Bào Liên Quan
• Sử Dụng Bộ Điều Khiển Anfis Thay Cho Bộ Điều Khiển Nfc
• Điều Khiển Mượn Kênh Động Phân Tán Trên Cơ Sở Mạng Nơ Ron–Mờ-Subsethood
• Về một phương pháp mới điều khiển mượn, khóa kênh tần số mạng di động tế bào - 12
• Khối Thực Hiện Quá Trình Mượn/cho Mượn Kênh Và Khóa Kênh.
• Phát Sinh Tập Dữ Liệu Huấn Luyện Và Huấn Luyện Anfis, Nfs, Nfc

Xem toàn bộ 149 trang tài liệu này.

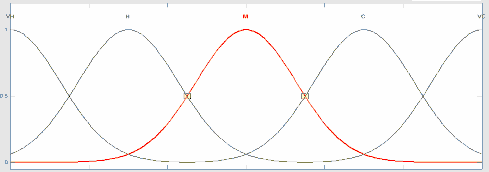
Với các giá trị biến ngôn ngữ đầu ra: { NVL, NL, NM, NS, AZ, PS, PM, PL, PVL} sử dụng hàm liên thuộc là hàm Gauss, quan hệ giữa đầu ra mờ và khoảng giá trị giải mờ [-d, d] thể hiện như hình 3.5.

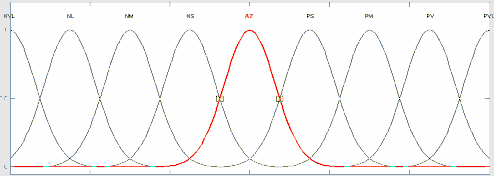
-d 0 +d Hình 3.5. Các tập mờ đầu ra với hàm liên thuộc Gauss

Giá trị đầu ra bộ giải mờ càng âm có nghĩa số kênh của tế bào có khả năng cho các tế bào khác mượn càng nhiều. Ngược lại, giá trị giải mờ càng dương, có nghĩa tế bào cần mượn số kênh càng nhiều. Còn giá trị xấp xỉ bằng 0 (AZ) thì tế bào không thực hiện hoạt động mượn kênh/cho mượn kênh với các tế bào lân cận.

Thiết kế bộ điều khiển NFS để phát sinh tập luật mờ:

Cơ sở luật mờ được đặc trưng bởi tập mờ IF-THEN thu được mà trong đó phần điều kiện và phần kết luận là các biến ngôn ngữ. Tập các luật mờ này đơn giản là thể hiện quan hệ vào/ra của hệ thống. Dạng chung của luật điều khiển mờ trong trường hợp MISO gồm 2 đầu vào một đầu ra có dạng sau:

Ri: IF X is Ai AND Y is Bi , THEN Z is Ci i=1,2,...,n (3.12)

Với x, y, z là các biến ngôn ngữ biểu diễn các biến điều khiển tương ứng. Còn Ai , Bi, Ci là các giá trị ngôn ngữ của các biến x, y, z tương ứng. Tập luật mờ này có thể thu được sử dụng một trong 2 phương pháp:

 Sử dụng tri thức chuyên gia

 Phát sinh tập luật dựa vào tập dữ liệu huấn luyện

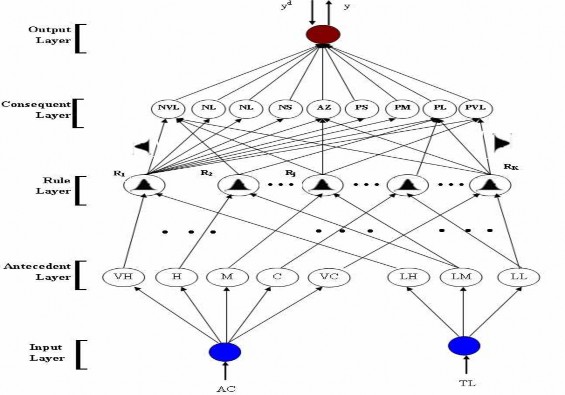
Hình 3.6: Cấu trúc mạng nơ ron mờ sử dụng subsethood (NFS)

Trong bộ điều khiển DBNFS, NFS thực hiện thu tập luật mờ IF-THEN tự động bằng cách sử dụng mạng nơ ron mờ, với liên kết mờ dùng phép đo subsethood để đo định lượng mức độ đóng góp của phần IF lên phần THEN của mỗi luật mờ. Việc sử dụng các liên kết mờ cho phép thu được tập luật mờ có chất lượng tốt hơn. NFS gồm 5 lớp (Hình 3.6) [57][58][59]: Lớp 1 là lớp vào, lớp 2 là lớp điều kiện, mỗi nút là một giá trị ngôn ngữ của biến vào. Lớp 3 là lớp luật. Lớp 4 là lớp biểu diễn phần kết luận của luật, mỗi nút là một nhãn ngôn ngữ của biến ra và nó cũng thực hiện giải mờ tại mỗi nút này. Lớp 5 là lớp đầu ra. Các nút lớp 2, 3 đều sử dụng hàm thành viên mờ dạng Gauss. Điểm đặc biệt của mạng nơ ron mờ này so với các mạng nơ ron mờ khác là nó sử dụng các liên kết mờ đầy đủ giữa lớp luật và lớp mệnh đề kết luận. Các liên kết mờ này thể hiện mức độ tác động của mỗi phần điều kiện trong mỗi luật đến phần kết luận như thế nào. Mỗi liên kết mờ cũng sử dụng hàm thành viên mờ dạng Gauss và xác định mức độ giống nhau giữa nó với tập mờ của luật Rk tương ứng bằng cách sử dụng phép đo subsethood mờ. Mạng đầu vào và ra của mỗi nút trong các lớp được trình bày trong bảng 3.2. Với tín hiệu đầu vào x1 là AC được mờ hoá thành các tập mờ {VH, H,M,C,VC}, x2 là TL được mờ hoá thành các tập mờ {LL, ML, HL}. Dữ liệu huấn luyện

mạng để phát sinh tập luật mờ là cặp dữ liệu {x, yd }, trong đó x=(AC, TL), yd là số

kênh đầu ra mong muốn.

Bảng 3.2: Mạng đầu vào và ra của các lớp của NFS

Lớp

Tên lớp	Mạng đầu vào	Mạng đầu ra
1	Input layer	f (1) x i i	y(1) f (1) i i
2	Antecedent layer	f n (x c n ) / n (2) (1) 2 2 ILi i i ILi i ILi i	( 2 ) (1) 2 2 f ni ( xi c ni ) /ni x(2) e ILi e ILi ILi ILni i
3	Rule layer	N k ILni k ,ILni f (3) x(2)  i1 i i	x(3) e( f ( 3) ck )2 /2 k k k

4

Consequent layer	f ( 4) x(3)(, R ) OLm ,k k OLm k	K x(4) ( f (4) c ) / k OLm ,k OLm ,k OLm ,k k 1 K (fOLm,kOLm,k ) ( 4)  k 1
5	Output layer	M f mOLm (5) x( 4) m1	x(5) y f (5)

Trong đó:

XT=[x1, x2]=[AC, TL] : véc tơ đầu vào

(k)

fi : Mạng đầu vào của nút thứ i, lớp thứ k

(k)

xi : Đầu ra của nút thứ i, lớp thứ k

ni

ILi : Giá trị ngôn ngữ thứ ni của biến vào xi với hàm thành viên dạng Gausian

định nghĩa là:

ILni

 (c ,

) với tâm c và độ trải (nút của lớp 2).

i ILni

ILni

ILni

ILni

i i i i

ωk, ILini: Là trong liên kết từ lớp điều kiện đến lớp luật. Nó xác định trọng số đóng góp của nút ngôn ngữ ILnii(i=1,2,...N và ni thuộc Ni ) cấu thành phần IF của luật mờ Rk.

Rk : Luật mờ IF-THEN thứ k và là một nút của lớp 3 dùng hàm thành viên Gausian được định nghĩa là Rk(ck, σk).

OLm: Là một nút của lớp 4. Mỗi nút biểu diễn một giá trị ngôn ngữ thứ m của biến đầu ra y.

νOLm,k : Trọng liên kết mờ từ nút luật Rk tới giá trị ngôn ngữ đầu ra OLm. Nó cũng sử dụng hàm thành viên dạng Gauss với tâm νcOLm,k và hệ số độ trải νσOLm,k và được định nghĩa bởi νOLm,k(νcOLm,k ,νσOLm,k ).

ε(νOLm,k, Rk): Phép đo subsethood tương hỗ trọng liên kết mờ. Nó đo mức độ giống nhau của các tập mờ để định lượng mức độ tác động của luật mờ Rk lên phần kết luận OLm. Phép đo subsethood sử dụng được định nghĩa như sau [33]:

S( A, B) M ( A B)

M ( A B)

(3.13)

Trong đó A, B là các tập mờ thuộc không gian U. S(A,B) là subsethood đo mức

độ mà A là tập con của B, với

S ( A, B) [0,1].

ξm: là trọng số từ giá trị ngôn ngữ đầu ra OLm tới nút lớp đầu ra.

Tính subsethood cho liên kết mờ giữa lớp 3 và lớp 4[57][58]:

Xét liên kết mờ giữa luật Rk với nút giá trị ngôn ngữ của lớp 4 là OLm. Trọng liên kết mờ mô tả mức độ tác động của các luật lên các giá trị ngôn ngữ đầu ra và nó được đo

OL ,k OL ,k

bởi subsethood tương hỗ (m , Rk ) . Hay nói cách khác (m , Rk )

đo sự giống nhau

giữa các luật mờ Rk và tập mờ 

OLm ,k

[33]. Từ định nghĩa subsethood (3.13) chúng ta

OL ,k k

xác định được subsethood tương hỗ (m , R ) như sau:

(

C(m Rk )

, R ) OL ,k 

C(m Rk )

(3.14)

OL ,k

OLm ,k k

C(

OLm ,k

Rk )

C(

OLm ,k

) C(Rk ) C(

OLm ,k

Rk )

OL ,k k

với (m , R ) [0,1] .

Vấn đề ở đây là phải tính được

(

OLm ,k

, Rk ) ,

(m , R , )



OL ,k k

C

OLm ,k

(m , R , )



.

OL ,k k

và 

OLm ,k

Với các tập mờ

OLm,k

và Rk sử dụng hàm liên thuộc dạng Gauss tương ứng là

exp((( x C ) /)2 ) và exp((x C ) / )2 ) thì các yếu tố C() của tập mờ

OLm ,k OLm ,k k k OLm ,k



OLm,k

và C(Rk) của tập mờ Rk có thể được định nghĩa như sau:

) exp((( x C

OL

,k

C(m

) /

)2 )dx

(3.15)

m



OL ,k OL ,k



m

C(R )  exp((x C ) / 

)2 )dx

(3.16)

k k k

OLm ,k

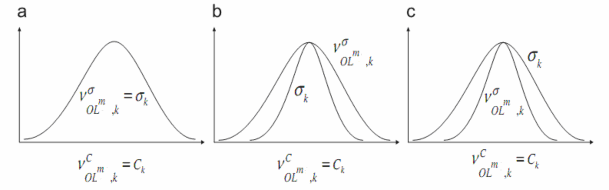
Hình 3.7: Trường hợp 1:C =Ck

Quan hệ giữa trung tâm và độ trải của tập mờ

hợp:

OLm,k

và tập mờ Rk xẩy ra 3 trường

 Trường hợp 1:C =C , 2 tập mờ và R

giống nhau (thuộc về nhau) và

OLm ,k k OLm ,k k

OLm ,k

có thể xẩy ra 3 trương hợp với 



:

OLm ,k

k



, 

OLm ,k

k



, 

OLm ,k

k .

Với các yếu tố của 2 tập mờ sử dụng hàm sai số chuẩn



định được:

erf (x) 

1 x

2

t2 / 2

e dt

0

thì xác

C(



) 

OLm ,k OLm ,k

(3.17)



C(Rk ) k

OL ,k

OL ,k OL ,k

Từ đó ta xác định được C(m Rk )

đối với 3 trường hợp khác nhau:

(3.18)



OL ,k

- C(m Rk ) :

C(m Rk ) C(m ) C(Rk )

(3.19)

- 



OLm ,k

k

: C(

OLm ,k

Rk ) k

(3.20)



- C(

R ) 

(3.21)

OLm ,k k OLm ,k

Thay (3.17)-(3.19) vào phương trình (3.14) thu được kết quả sau: