Về một phương pháp mới điều khiển mượn, khóa kênh tần số mạng di động tế bào - 12

1 if



C



OLm ,k

Ck and

Có thể bạn quan tâm!

• Sử Dụng Bộ Điều Khiển Anfis Thay Cho Bộ Điều Khiển Nfc
• Điều Khiển Mượn Kênh Động Phân Tán Trên Cơ Sở Mạng Nơ Ron–Mờ-Subsethood
• Về một phương pháp mới điều khiển mượn, khóa kênh tần số mạng di động tế bào - 11
• Khối Thực Hiện Quá Trình Mượn/cho Mượn Kênh Và Khóa Kênh.
• Phát Sinh Tập Dữ Liệu Huấn Luyện Và Huấn Luyện Anfis, Nfs, Nfc
• S. W. Halpern (1983), “Reuse Partitioning In Cellular Systems”, Proceeding Of The 1983 33Rd Ieee Vehicular Technology Conference, Pp. 322-327, New York, Ny, Usa.

Xem toàn bộ 149 trang tài liệu này.





OLm ,k

k

(

, R ) /if C C and 

(3.22)



OLm ,k k k OLm ,k OLm ,k k

OL ,k

C

OLm ,k k

OL ,k



OLm,k /k

if m Ck

and

m k



C

(

OLm ,k

OLm ,k

, Rk )  0



if

C

OLm ,k

Ck

(3.23)

0 if



C



OLm ,k

Ck and





OLm ,k

k

(

, R ) 

/ (

)2 if C C and 

(3.24)



C

OLm ,k

OLm ,k k k



OLm ,k

OLm ,k k

OLm ,k k

1 / k

C



if

OLm ,k

Ck and





OLm ,k

k

OLm ,k

 Trường hợp 2:C

Ck

, hai tập mờ m và Rk

giao nhau và cũng xẩy ra 3

OL ,k

OLm ,k

trường hợp: 

k



, 

OLm ,k

k



, 

OLm ,k

k .

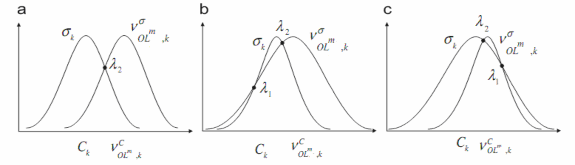
OLm ,k

Hình 3.8: Trường hợp 2:C C

k

Trong trường hợp này phải xác định được điểm giao nhau bằng cách đặt 

thu được 2 điểm giao nhau:

OLm ,k

=Rk

 (C C ) / ()

(3.25)

1 OLm ,k k k OLm ,k OLm ,k k

 (

C C

) / ()

(3.26)

2 OLm ,k

k k OLm ,k

OLm ,k k

OL ,k

Tương tự trường hợp trên, chúng ta xác định được C(m Rk ) :

- 





OLm ,k

k :

C(

R ) 

erf ( 2(

C

) /

 1 / 2



OLm ,k k

OLm ,k 

2 OLm ,k

OLm ,k 

C(

R ) 

erf ( 2(

C

) /

 1 / 2

(3.27)

OLm ,k k

OLm ,k 

2 OLm ,k OLm ,k 



- 





OLm ,k

k :

k

1 / 2 erf ( 2(2 Ck ) / k )

C(

R ) 1 erf (( 2(

C ) / 

) erf (( 2(C ) / )



OLm ,k

k k 

1 k k

2 k k 



erf (( 2(

C

) /

) erf (( 2(

C

) /

)(3.28)



OLm ,k 

- 



:



OLm ,k k

2 OLm ,k OLm ,k

1 OLm ,k OLm ,k 

C(

R ) erf (( 2(

C ) / 

) erf (( 2(C ) / )



OLm ,k

k k 

1 k k

2 k k 



1 erf (( 2(

C

) /

) erf (( 2(

C

) /)

(3.29)



OLm ,k 

2 OLm ,k OLm ,k

1 OLm ,k OLm ,k 

Thay kết quả trên vào (3.14) thu được kết quả:



 ((, R )) (3.30)

C OLm ,k

OLm ,k

(C(m R ))



OL ,k k 

k

(

) C(





R )



(

OLm ,k

k ) C(

OLm ,k

R )

k C(

R )

C

OLm ,k

OLm ,k k

OLm ,k

k 

OLm ,k

2

OLm ,k k

() C(R )

OLm ,k k OLm ,k k 

 ((



OLm ,k

, Rk )) (3.31)

OLm ,k

(C(m R ))

OL ,k k 

(

) C(





R )



(

OLm ,k

k ) C(

OLm ,k

R )

k C(

R )





OLm ,k

OLm,k k

OLm,k

k 

OLm,k

2

OLm,k k

Trong đó:



(

OLm ,k

k ) C(

OLm,k

R )

k 

exp(((C

)/

)2) if 

(C(

R )) 

2 OLm ,k OLm ,k OLm ,k k

OLm,k

k exp(((C

)/

)2)exp(((C

)/

)2) if 

(3.32)



C 

OLm,k 

1 OLm ,k OLm ,k

2 OLm ,k

OLm,k

OLm ,k k

exp(((C

)/

)2)exp(((C )/

)2) if 

1 OLm ,k

OLm,k

2 OLm ,k OLm ,k

OLm ,k k

OL ,k

(m , Rk ) (3.33)

i:

OLm,k k

erf ( 2(C

) /

) 1/ 21/ 2erf (( 2(C ) /)

OLm ,k 

2 OLm ,k OLm ,k

k 

2 k k 



1/ 2erf (( 2(C

) /)1/ 2erf (( 2(C ) /)

OLm ,k

2 OLm,k

OLm ,k k 

2 k k 

? 



iOLm,k k:



 ( 2(C ) 

 ( 2(C

) 

 ( 2(C

)  ( 2(C

) 



erf 

2 OLm ,k

erf 

1 OLm,k

1erf 

1 OLm ,k

erf 

2 OLm ,k 

OLm ,k 



k 









OLm ,k 



 ( 2(C ) 

( 2(C

)



 ( 2(C

)

 ( 2(C ) 





OLm,k



k 

k 





1erf 

2 OLm ,k

erf 

1 OLm ,k



erf 

1 OLm ,k

erf 

1 OLm ,k 





OLm,k 







OLm ,k





OLm ,k

k 

k

k





i:

OLm ,k



k

 ( 2(C ) 

 ( 2(C

) 

 ( 2(C 

 ( 2(C 



1erf 

2 OLm ,k

erf 

1 OLm,k



erf 

1 OLm ,k erf 

2 OLm ,k 

OLm ,k 





k 





OLm ,k 

OLm,k



k 

k 

( 2(1 Ck)

( 2(2 Ck

 ( 2(C ) 

m

 ( 2(C

m

) 





erf 1 OL ,kerf 

2 OL ,k



1erf

erf

OLm ,k 



k 





OLm ,k 

OLm ,k



k 

k 



OL ,k k

(C(m R ))





OLm ,k

(3.34)









1

C ) C

m

m



2 (2 

2 









erf 

OL ,k



OL ,k exp((

C

) / 

)2 if 



 2



C



OLm ,k



OLm ,k



C

2 OLm ,k OLm ,k OLm ,k k

1 OLm ,k exp(((

C

) / 

)2 ) 2

OLm ,k exp(((

C

) / 

)2 )



1 OLm ,k OLm ,k 

2 OLm ,k OLm ,k

OLm ,k OLm ,k

if 



2 (

C

) 

2 (

C

) 

OLm ,k k



1erf 

2 OLm ,k

erf 

1 OLm ,k 





 2









C





OLm ,k 



OLm ,k 

C

1 OLm ,k exp(((

C

) / 

)2 ) 2

OLm ,k exp(((

C

) / 

)2 )



1 OLm ,k

OLm ,k 

2 OLm ,k OLm ,k

OLm ,k OLm ,k



if 

C

C OLm j ,k

 2 (2 m )  2 (m

) j



1 erf 

k





OL ,k

erf 

1 OL ,k 



 2 







OLm ,k



OLm ,k 

 Trường hợp 3:C C , trường hợp này hai tập mờ và R

giao nhau và cũng

OLm ,k k

OLm ,k k

OLm ,k

xẩy ra 3 trường hợp: 

k



, 

OLm ,k

k



, 

OLm ,k

k

tương tự như trường hợp 2.

Điểm giao nhau của 2 tập mờ Hình 3.9:

OLm,k

và Rk cũng được xác định và thể hiện như

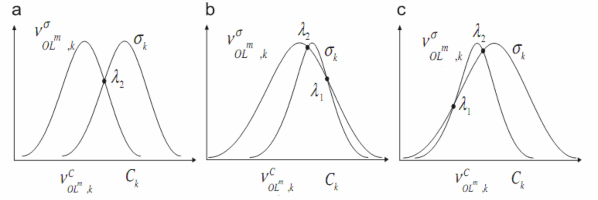
OLm ,k

Hình 3.9: Trường hợp 3:C C

k

Bằng cách tính tương tự như trường hợp 2, chúng ta cũng thu được kết quả của các

OL ,k OL ,k

biểu thức C(m Rk ) , (m , Rk ) ,

(C(m R ))



OL ,k k

C ,

OLm ,k

(C(m R ))



OL ,k k

.

OLm ,k

Sau khi xác định được cách tính các liên kết mờ, luận án sẽ đề xuất thuật cập nhật tham số cho NFS trong phần tiếp theo.

Thuật cập nhật tham số cho các lớp NFS:

Giả sử NFS đựơc huấn luyện bởi cặp dữ liệu vào ra ( x

(), yd ()) . Giả sử gọi

y(τ) là tín hiệu đầu ra thực sự , hàm giá E của mạng được định nghĩa như sau:

E() 1 ( yd y())2

2

(3.35)

Với mạng nơ ron trên, các tham số mạng NFS được cập nhật đến giá trị tối ưu theo thuật giảm Gradient. Công thức cập nhật tham số và trọng liên kết của các lớp như sau: Lớp 5:

( 1) () (E() / c

())

(3.36)

Lớp 4:

m m OLm ,k

( 1) () (E() / 

())

(3.37)



OLm ,k OLm ,k OLm ,k

OLm ,k

OLm ,k

Lớp 3:

c OLm ,k

( 1) c

() (E() / c

())

(3.38)

ck ( 1) ck () (E() / ck ())

k ( 1) k () (E() / k ())

(3.39)

(3.40)

Lớp 2:

n ( 1) 

k ,ILi i

n () (E() / 

k ,ILi i

n ())

k ,ILi i

(3.41)

c n ( 1) c

ILi i

n () (E() / c

ILi i

n ())

ILi i

(3.42)

n ( 1) 

ILi i

n () (E() / 

ILi i

n ())

ILi i

(3.43)

Với η là hằng số học, τ là bước thời gian.

Trong đó các đạo hàm trong các phương trình tham số được xác định như sau:

E E . y

(d

y )x(4)

(3.44)

y 

OLm

m m

E

C

E

y

y

x( 4)

( 4)

x

OLm ,k

C

E

y

y

x(4)

( 4)

x

OLm 

C

(3.45)

OLm ,k OLm

OLm ,k OLm

OLm ,k

K ( f (4) C )

K( f (4) )

1 1

K (4) 

k1 OLm,k OLm,k OLm,k

K (4) C 

k1 OLm ,k OLm,k

k(fOLm,k.OLm,k )

C

k(fOLm,k.m

.m )

C

OL ,k OL ,k

2

m

(d y )

OLm ,k OLm ,k

K ( f (4) )

k1 OLm,k OLm,k 



K ( 4) C 

(R ,)

3 OL ,k

k m



( 4) 

2

(d

y )

k 1 (fOLm,k .OLm,k )OLm,kOLm,k xk



m



C



OLm ,k

f m m 

OL ,k OL ,k 

K ( f ( 4) )

k 1 OLm,k OLm,k 

K ( 4) C

(R ,) 



(3) OL ,k

k m

k 1 (fOLm,k .OLm,k .OLm,k )OLm,k xk



k m



2

C

OLm ,k 

K ( f ( 4) )

k 1 OLm,k OLm,k 

E E y

( 4)

x

OLm

E y

( 4)

x

OLm

= (3.46)



y x( 4)



y x( 4)



OLm ,k



K

OLm



OLm ,k OLm

OLm ,k

((

m , Rk )

q1

OLm ,q OLm ,q

k OLm ,k OLm ,k

k k OLm ,k OLm ,q



m 

(d



y )

( f (4) 

). x(3)C



(

, R ) x(3)C 

2

OL ,k 

OLm ,q 

k 1

OLm ,q OLm ,q 

K



( f (4) )



k



k



K ( f (4) C 

) x(3)(, R ) x(3) ((, R ))

q1



OLm ,q OLm ,q OLm ,q





OLm ,k

K ( 4)

k k OLm ,k 

OLm ,q

2

OLm ,k 





E

Ck

E

y

M

.

m1

y

m

x( 4)

OL

(4)

x

. OLm

m

f ( 4)

OL ,k

(4)

f

OLm ,k

Ck

k 1 (fOLm,qOLm,q )







C 

( K f ( 4) 

) 

( K f ( 4) C 

)

. 

OLm ,k

OLm ,k

q1

OLm ,q

OLm ,q

OLm ,k

q1

OLm ,q

OLm ,q OLm ,q 

m (

M

K f ( 4) )2 



(d

y ) 

q1 OLm,q OLm,q

 ( f ( 3) c )2 

(3.47)



m 1 

(m

, Rk ) 2( f (3) c )

k k 

2

. x(3)

OL ,k

k k

.e k (, R ) 

k



2

Ck (k )

OLm ,k k 



E

k

E

y

M

.

m1

y

m

x( 4)

OL

( 4)

x

.OLm

m

f ( 4)

OL ,k

( 4)

f

. OLm ,k 

k

C 

( K f ( 4) 

) 

( K f ( 4) C 

)

. 

OLm ,k OLm ,k

q1

OLm ,q

OLm ,q OLm ,k

q1

OLm ,q OLm ,q

OLm ,q 

m (

M

K f (4) )2 



(d

y ) 

q1 OLm,q OLm,q

 ( f ( 3) c )2 

(3.48)



m 1 

(m

, Rk ) 2( f (3) c )

k k 

2

. x(3)

OL ,k

k k

.e k (, R ) 

k



2

k (k )

OLm ,k k 



E E M y

x( 4)

f ( 4)

x3

f (3)

OLm

OLm ,k k k 

(3.49)

y

x( 4)

f ( 4)

x3

f (3) 

k ,ILni

m1

OLm

OLm ,k k k

k ,ILni

i i

C 

( K f ( 4) 

) 

( K f (4) C 

)



m



OLm ,k OLm ,k

q1

OLm ,q

OLm ,q OLm ,k

q1

OLm ,q OLm ,q

OLm ,q 



(

K



M

q1

(4)

f

m j

2 



)

OLm ,q

(d

y ) 

m 1 

 ( f ( 3) c )2 

OLj ,q 





2

k k

e k



(

2( f (3) c ) 



, R )x( 2)k k

i

2

OLm ,k



k ILni

(k ) 

E E M y

K x( 4)

f (4)

x3

K f (3) x( 2)

f ( 2)



OLm

OLm ,l

l k

ILni

ILni 

(3.50)

C y

x( 4)

f ( 4)

x3

f (3)

x( 2)

i i

f ( 2) C

ILni

m 1

OLm

l 1

OLm ,l

l l k 1

ILni

ILni

ILni

i i i i

C 

K ( 4 ) 



K ( 4 ) C 

O Lm ,k O Lm ,k fO Lm ,q O Lm ,q O Lm ,k ( q 1 fO Lm ,q O Lm ,q O Lm ,q ) 

q 1 

( K f ( 4 ) ) 2 

M 

q 1

O Lm ,q O Lm ,q 

( d y

) m



m 1 

 ( f l( 3 ) cl )2 

( 3 )

( 2 )

(1) 2 

2 

K f

2( x C n ) 

e i

l

k 1

2( f

c )

ni i IL i





.(

m , R )e 

l l l.

IL .i

n

O L ,l l



() 2

k , ILi i



2 

ILni

i 

E E M y

K x( 4)

f ( 4)

x3

N f (3) x(2)

f ( 2)



OLm

OLm ,l

l k

ILni

ILni 

(3.51)

y

x( 4)

f ( 4)

x3

f (3)

x( 2)

i i

f (2) 

ILni

m 1

OLm

l 1

OLm ,l

l l k 1

ILni

ILni

ILni

i i i i

C 

K ( 4 ) 



K ( 4 ) C 

m m 

O Lm ,k O Lm ,k fO L ,q O L ,q O Lm ,k ( q 1 fO Lm ,q O Lm ,q O Lm ,q ) 



q 1 

K

( 4 ) 2 

 ( d

M

y ) m





( q 1 fO Lm ,qO Lm ,q )





m 1 

 ( f l( 3 ) C l )2 

( 3 )

( 2 )

(1) 2 

2 

K f

2( x C n ) 

e i

l

k 1

 2( f

C )

ni i IL i





.(

m , R )e 

l l l.

IL .i

n

O L ,l l



() 2

k , ILi i



3 

ILni

i 

Với các biểu thức của ε và đạo hàm ε đã được xác định trong phần liên kết mờ (trình bày phần trên). Thuật cập nhật trong quá trình huấn luyện mạng với mẫu huấn luyện

{x, yd} sẽ thực hiện như sau:

Luật mờ có dạng:

j

j

j

R : IF x is AIL1and ... x is AILiand x is AILN

THEN y is yk with

j (3.52)

j 1 1 i i N N

Cơ chế suy diễn: Cơ chế suy diễn của NFS không sử dụng phép toán t-norm và nó có dạng sau(hình 3.10):

Input: IF x1 is A1 and ... xN is AN

------------------------------------------------------------------------------------------------------------------------------------------------------------

R : IF x

is AIL1

and ... x

is AILi

and x is

AILN

THEN y is yk with 1

1

1

1

1 1 1 i i N N

...............................

Xem tất cả 149 trang.