Sử Dụng Bộ Điều Khiển Anfis Thay Cho Bộ Điều Khiển Nfc

y * 

M





j 1

j 1

M

Có thể bạn quan tâm!

• Thuật Toán Cân Bằng Tải Động Mượn Kênh Chọn Lọc (Lbsb)
• Mượn, Khóa Kênh Động Trên Cơ Sở Bộ Điều Khiển Logic Mờ Và Mạng Nơ Ron
• Pha Thỏa Thuận Với Tế Bào Liên Quan
• Điều Khiển Mượn Kênh Động Phân Tán Trên Cơ Sở Mạng Nơ Ron–Mờ-Subsethood
• Về một phương pháp mới điều khiển mượn, khóa kênh tần số mạng di động tế bào - 11
• Về một phương pháp mới điều khiển mượn, khóa kênh tần số mạng di động tế bào - 12

Xem toàn bộ 149 trang tài liệu này.

j w j

j



(2.25)

Với:

j A j (x1 )A j (x2 )...A j (xn )

(2.26)

1 2 n

Đầu ra của bộ suy luận mờ y có thể được tính bằng phương trình (2.25) và (2.26). Từ đó số kênh cho phép di chuyển cũng được xác định bằng công thức:

Y

o COA

y* IN (c)

(2.27)

Vấn đề đặt ra là làm thế nào để tối ưu tập luật thông qua học tham số của bộ điều khiển mạng nơ ron mờ NFC với một tập dữ liệu huấn luyện cho trước. Quá trình

này được thực hiện bằng cách điều chỉnh hàm liên thuộc đầu vào j

Ai

và số thực wj.

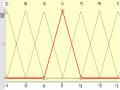
Hàm liên thuộc có thể sử dụng dạng hàm Gauss, dạng hình thang, dạng tam giác.... Để

đơn giản, giả sử hàm liên thuộc đầu vào j

Ai

sử dụng có dạng tam giác (hình 2.6).

2 x a j

i i

(x )  1(2.28)

b

Aij i j

i

(x )

Ai

j i

1

0.5

ai

j

0

bj

i

xi

Hình 2.6: Hàm liên thuộc hình tam giác cân

a

i

với i=1,2,.., n; j=1,2,..,M. Tham số cần xác định cho tam giác là giá trị tâm j và độ

i

rộng b j  0 . Mục tiêu huấn luyện mạng nơ ron- mờ là tìm tham số hàm liên thuộc mờ

a

i

i

tối ưu: j và b j . Với hàm mục tiêu được định nghĩa như sau:

E 1 ( y yd )2 2

(2.29)

với y là tín hiệu đầu ra thực sự, yd là tín hiệu đầu ra mong muốn. Theo phương pháp giảm gradient, các tham số hàm liên thuộc hình tam giác sẽ được cập nhật theo các biểu thức sau [48]:

a j (t 1) a j E

i

i i a a j

b j (t 1) b j E

i

i i b b j

(2.30)

(2.31)

w (t 1) w

E

(2.32)

j

j j w w

2.3. Đánh giá các thuật toán FDCBS và NFDCBS

Kết quả thuật toán FDCBS và NFDCBS [47][48] đã khắc phục được hạn chế của các thuật toán dựa trên giá trị ngưỡng phân biệt trạng thái tải tế bào, nhất là hiện tượng hiệu ứng quả bóng bàn. Thuật toán NFDCBS cho phép phát sinh tập luật trên cơ sở mạng nơ ron mờ với tập dữ liệu huấn luyện, từ đó ít phụ thuộc vào tri thức chuyên gia hơn FDCBS. Yao-Tien Wang [47][48] đã khảo sát và chứng minh rằng FBCBS và NFDCBS cho xác xuất khóa kênh, xác suất rớt cuộc gọi, mức độ phức tạp truyền thông điệp và thời gian trễ thu kênh là tốt hơn các thuật toán truyền thống như CBWL, LBSB, Adapt, DR... .

Tuy nhiên các thuật toán FDCBS và NFDCBS cũng còn tồn tại nhiều hạn chế:

Thứ nhất với bộ điều khiển FDCBS sử dụng tập luật mờ thiết kế trên cơ sở tri thức chuyên gia nên:

- Phụ thuộc mạnh vào tri thức chuyên gia

- Tập luật còn quá nhiều luật và chưa tối ưu

- Hạn chế khả năng xấp xỉ do bản chất của việc xây dựng tập luật điều khiển mờ.

- Việc tính toán phức tạp và tốn thời gian.

Tương tự với bộ điều khiển NFDCBS: Mặc dù khắc phục được sự phụ thuộc mạnh vào tri thức chuyên gia và tối ưu được hàm liên thuộc của tập mờ, nhưng NFDCBS cũng còn các hạn chế sau:

- Việc sử dụng mạng nơ ron mờ với quá trình huấn luyện online đòi hỏi mất nhiều thời gian và cần tài nguyên máy tính mạnh mới đáp ứng được thời gian thực.

- Hạn chế độ chính xác do chưa đánh giá được mức độ đóng góp của phần giả thiết lên phần kết luận trong mỗi luật mờ.

- Toán tử t-norms và t-cornom có thể chọn theo nhiều cách khác nhau nên việc tối ưu toán tử là cần thiết khi thiết kế tập luật bởi mạng nơ ron. Nhưng thuật toán NFDCBS chưa thực hiện được điều này.

- Bộ điều khiển mạng nơ ron NFC cho tập luật kiểu Mandani nên hạn chế mức độ

chính xác.

Một điểm hạn chế nữa trong các thuật toán FDCBS và NFDCBS là chưa chỉ ra chiến lược chọn kênh cụ thể. Điều này là cực kỳ quan trọng trong việc mượn kênh, di chuyển kênh để cân bằng tải động. Vì khi chọn tế bào mượn kênh cần phải đánh giá mức độ khóa kênh, số tế bào đồng kênh cần khóa kênh, khoảng cách giữa tế bào mượn kênh và tế bào cho mượn kênh...là những tham số ảnh hưởng trực tiếp tới khả năng kênh của toàn mạng và chất lượng dịch vụ. Chính vì vậy sau đây chúng tôi sẽ thực hiện một số cải tiến thuật toán NFDCBS của Yao-Tien Wang, nhằm nâng cao chất lượng dịch vụ của mạng.

2.4. Một số cải tiến thuật toán mượn kênh NFDCBS

2.4.1. Sử dụng bộ điều khiển ANFIS thay cho bộ điều khiển NFC

ANFIS là bộ điểu khiển nơ ron mờ với luật mờ kiểu TSK và có nhiều ưu điểm hơn so với mạng nơ ron NFC đề xuất bởi [48]. Nó cho hiệu suất cao hơn và độ chính xác cao hơn NFC khi giải quyết cùng bài toán. Bộ điều khiển ANFIS có cấu trúc và cơ chế suy diễn có thể được mô tả như hình 2.7. Luật mờ TSK Rj của ANFIS có dạng:

Rj: IF x1 is A1j AND x2 is A2j AND.....AND xn is Anj

j

i

THEN y=fj=aoj +a1jx1+...+anjxn (2.33) Trong đó xi là biến vào, i=1,2,..,n ; y là biến ra; Ai là các đại lượng ngôn ngữ phần điều

kiện có hàm thành viên

Aij

(xi ) ,

a j R

là các hệ số của phương trình tuyến tính

fj(x1,x2,...,xn) với j=1,2,.., M; i=1,2,..,n. Cấu trúc ANFIS sử dụng thay NFC trong bộ điều khiển gồm 6 lớp có thể mô tả như sau (Hình 2.7b):

Lớp 1: Lớp đầu vào chỉ đóng vài trò truyền tín hiệu đầu vào mạng

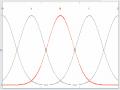
Lớp 2: Mỗi nút trong lớp này phát sinh mức độ thành viên của nhãn ngôn ngữ. Hàm liên thuộc (giả sử dạng hình chuông) của nút thứ i có dạng:

i A

O2 

i

( x) 

1  (( x

1

ri)2)qi

với i=1,2 (2.34)

pi

Với x là đầu vào của nút, Ai là nhãn ngôn ngữ liên kết với nút. {x; pi,ri} là tập tham số của hàm liên thuộc.

Lớp 3: Mỗi nút trong lớp này tính trọng số của mỗi luật thông qua phép tính tích và các nút là cố định:

i i

O3 (x )(x ) với i=1,2 (2.35)

2

A1 1 A 2

i i

Lớp 4: gồm các nút cố định. Chúng được đánh nhãn với N chỉ thị rằng chúng biểu diễn vai trò chuẩn hoá đối với cường độ từ lớp trước. Đầu ra của lớp có thể biểu diễn:

i i



O4 i



với i=1,2 (2.36)

1 2

x

x

x1 x

x2

x

A11

A21

A22

A12

µ1

f a1 a1 x a1 x





1 0 1 1 2 2

f 1 f1 2 f2

µ2 f

a2 a2 x a2 x

2 0 1 1 2 2

a)

Lớp 1 Lớp 2 Lớp3 Lớp4 Lớp 5 Lớp 6

1

1

1

A2

(x )

П

N

1 f1

A2

y*

1

1

1

Σ

A2

1

1 (x2 )

A2

П

N

f

2 2

A2



2

2

2

(x )

A2

2

x1 x2

A1

1

A 1

1 (x )

x1

x2

x1 x2

2

b)

Hình 2.7: a) Hệ thống suy diễn mờ ANFIS; b) Cấu trúc ANFIS

Lớp 5: gồm các nút thích nghi. Đầu ra của mỗi nút trong lớp này đơn giản là tích của cường độ chuẩn hoá và đa thức bậc nhất( đối với mô hình Sugeno bậc nhất), đầu ra của lớp này được xác định bởi công thức:

O5 f (ai ai x ai x )

với i=1, 2 (2.37)

i i i i 0 1 1 2 2

0 1 2

Với là đầu ra của lớp 3, ai, ai, ailà tập tham số. Các tham số trong lớp này sẽ qui về như các tham số phần kết luận.

Lớp 6: Chỉ có một nút ra cố định với nhãn Σ. Nút này thực hiện tổng hợp tất cả các tín hiệu đi đến. Từ đó đầu ra tổng thể của mô hình cho bởi:

O6 

2 μf

2

(

i1

i fi )

(2.38)

i i1 i i



1 2

Thuật học cơ sở của ANFIS cũng là thuật truyền ngược mà tính sai số tín hiệu phản hồi từ lớp ra về các nút của lớp 2. Từ cấu trúc ANFIS như hình vẽ 2.7 có thể thấy rằng với các giá trị các tham số biết trước, đầu ra toàn bộ f có thể biểu diễn như là tổ hợp tuyến tính của các tham số kết luận.

f f f (a1 a1x a1 x ) (a2 a2 x a2 x )

(2.39)

1 1 2 2 1 0 1 1 2 2 2 0 1 1 2 2

Phương pháp học ANFIS:

Mạng nơ ron sử dụng thuật BP để học hoặc điều chỉnh các trọng kết nối giữa các nơ ron từ tập mẫu huấn luyện I/O. Trong cấu trúc ANFIS, các tham số của phần điều kiện và phần kết luận biểu diễn vai trò của các trọng liên kết. Cụ thể hình dạng của hàm liên thuộc trong phần IF của các luật được xác định bởi các tham số hữu hạn. Các tham số này gọi là các tham số phần điều kiện, còn các tham số trong phần THEN của các luật qui về các tham số phần kết luận. ANFIS sử dụng cả BP và phương pháp ước lược bình phương tối thiểu (LSE) để điều chỉnh tập tham số trên. Cụ thể BP dùng để học phần điều kiện, còn LSE sử dụng để xác định các tham số phần kết luận của các luật. Mỗi bước trong thủ tục học gồm 2 pha: pha truyền thẳng và pha truyền ngược. Trong pha truyền thẳng, đầu ra và các tham số {ai,bi,ci} được ước lượng bởi phương pháp bình phương tối thiểu trong khi các tham số phần giả thiết được giữ cố định. Trong pha truyền ngược tín hiệu sai số được truyền ngược và BP được sử dụng để sửa chữa các tham số phần điều kiện {pi,qi,ri} trong khi các tham số phần kết luận được giữ cố định. Tổ hợp của các phương pháp bình phương tối thiểu và BP được sử dụng để huấn luyện các tham số hàm liên thuộc FIS của mô hình với một tập dữ liệu vào/ra.



n

k 1

( yd O )2

k

Hoạt động của hệ thống này sẽ được đánh giá sử dụng RMSE, căn bậc 2 của sai số bình phương (sự khác nhau giữa đầu ra FIS và đầu ra của dữ liệu huấn luyện/test):

RMSE 1

n

(2.40)

Với yd là đầu ra mong muốn, Ok là đầu ra thực sự, n là số mẫu huấn luyện/test.

Ngoài ra các tham số phần kết luận cũng có thể được tìm bằng cách sắp xếp tất

0 1 2 0 1 2

cả các tham số kết luận thành một véc tơ tuyến tính (2.41) với ràng buộc trên:

(a1 , a1, a1 , a2 , a2 , a2 )T

và giải hệ phương trình

a1 

(1) (1) (1) (1) (1) (1) (1) (1) (1) (1)

0 

1

1 x1

1 x2 2

2 x1

2 x2

a1

d (1) 

1 

(2) (2) (2) (2) (2) (2) (2) (2) (2) ( 2)

a1 

d (2)

1

1 x1

1 x2 2

2 x1

2 x2

2 

(2.41)

a2 

 .... 

............................................................................

0 

a2 

d ( p ) 

( p ) ( p ) x( p ) ( p ) x( p ) ( p ) ( p ) x( p ) ( p ) x( p ) 1 

2 

1 1 1 1 2

2 2 1 2 2

a2

với {x(k), d(k)} là các véc tờ vào và đầu ra mong muốn, k=1, 2,..., p.

2.4.2. Tối ưu tập luật mờ ANFIS

Sau khi thu được tập mờ (2.33) thì vấn đề quan trọng là phải thực hiện tối ưu tập luật mờ với tập dữ liệu huấn luyện cho trước. Việc tối ưu tập luật mờ có thể tối ưu tập tham số hàm liên thuộc đầu vào, tập tham số phần kết luận và tối ưu toán tử mờ bao gồm toán tử kết hợp, toán tử tổ hợp, toán tử kéo theo hoặc tối ưu tất cả các toán tử này. Việc thực hiện tối ưu tập luật được thực hiện thông qua các bộ điều khiển mạng nơ ron

mờ thích nghi ANFIS bằng quá trình huần luyện trình bày phần 2.3.1. ANFIS được huấn luyện bởi tập dữ liệu huấn luyện gồm p cặp dữ liệu mẫu {xk, dk }, với k=1,2..., p, sử dụng thuật truyền ngược BP. Trong đó xk ={AC(k), TL(k) } là véc tơ mẫu vào thứ k, dk là tín hiệu đầu ra mong muốn tương ứng với mẫu vào thứ k. Sự huấn luyện này có thể thực hiện offline, batch hoặc online để cuối cùng thu được tập tham số hàm liên thuộc mờ tối ưu nhất với sai số chấp nhận được. Tập luật tối ưu sau khi thu được từ quá trình

1 (1x ) / x  (1x ) / x





1 1







2 2





huấn luyện bằng thuật toán BP và LSE sẽ tiếp tục được tối ưu hoá toán tử mờ. Do toán tử phù hợp được chọn sử dụng trong bộ điều khiển logic mờ không phải là duy nhất đối với tất cả các ứng dụng, cho nên việc chọn toán tử mờ và tối ưu được nó là vấn đề quan trọng để nâng cao chất lượng bộ điều khiển nơ ron mờ. Toán tử có thể sử dụng là Dombi t-norm TD hoặc t-norms Hamachar TH có dạng [59]:

TD (, x1, x2 ) 

T (, x , x ) 

1

x1 x2

(2.42)

(2.43)

H 1 2  (1)(x x x x )

1 2 1 2

với xi là các hàm liên thuộc thành phần, là tham số không âm. Hoặc sử dụng toán tử trung bình tham số được đề xuất bởi Dyckhoff và Pedrycz[59]:

(xx)1/

M DP (, x1, x2 ) 1 2

2

(2.44)

với  1 và đối với một tập dữ liệu huấn luyện vào/ra, tham số trong các toán tử có

thể được điều chỉnh trong cùng cách như tham số khác trong mạng. Từ [59] chúng ta thu được cơ chế suy diễn toán tử mờ với tập luật cho ở bảng 2.1 dưới dạng phương trình (2.45).

T [VC ( AC), LL (TL), NL ( y)],T [M ( AC), LL (TL), NS ( y)], 

T [( AC), (TL), ( y)],T [( AC), (TL), ( y)], 

H LL AZ VH LL PS 





T [VC ( AC), LM (TL), NM ( y)],T [C ( AC), LM (TL), NS ( y)], 

( y) T * T [M ( AC), LM (TL), AZ ( y)],T [H ( AC), LM (TL), PS ( y)], 

T [( AC), (TL), ( y)],T [( AC), (TL), ( y)],

VH LM PM VC LH NS 

T [C ( AC), LH (TL), AZ ( y)],T [M ( AC), LH (TL), PS ( y)], 

T [( AC), (TL), ( y)],T [( AC), (TL), ( y)], 

H LH PM H LH PM 

T [VH ( AC), LH (TL), PL ( y)] 

(2.45)

Để tìm toán tử mờ tối ưu, luận án sử dụng mạng nơ ron huấn luyện với tập mẫu huấn luyện bằng thuật BP (Hình 2.8) với các đầu vào x1 là số kênh cho phép AC, x2 là