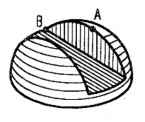
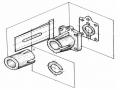
Ví dụ đầu trục xẻ rãnh (hình 4.6). Phần xẻ rãnh là giao tuyến của hai mặt phẳng song song với trục của hình trụ và một mặt phẳng vuông góc với trục hình trụ tạo thành.
4.1.3. Giao tuyến của mặt phẳng với hình cầu
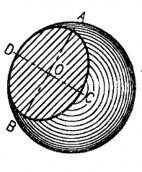
Giao tuyến của mặt phẳng với hình cầu là một hình tròn. Nếu hình tròn nghiêng với mặt phẳng hình chiếu, thì hình chiếu của hình tròn là elip (hình 4.7).
Nếu mặt phẳng cắt song song với mặt phẳng hình chiếu thì hình chiếu của đường tròn giao tuyến trên mặt phẳng đó cũng là đường tròn.
A1
D1 C1I1 F 1 E 1
B1
O1
A3
D2
I2
O2
C2
F2
B
E2
3
F2
D2
B2
I 2 O2
A2
E2
C2
Hình 4.7. Giao tuyến của mặt phẳng với hình cầu
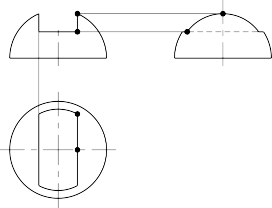
Ví dụ đầu đinh vít chỏm cầu xẻ rãnh (hình 4.8). Phần xẻ rãnh là do giao tuyến của hai mặt phẳng song song với mặt phẳng hình chiếu cạnh và một mặt phẳng song song với mặt phẳng hình chiếu bằng tạo thành.
A A3 1 B1 B3 B2 A2 | |
Hình 4.8. Hình chiếu của rãnh trên chỏm cầu |
Có thể bạn quan tâm!
-
Cách Vẽ Hình Chiếu Thứ Ba Từ Hai Hình Chiếu Của Điểm -
Đường Thẳng Và Điểm Thuộc Mặt Phẳng -
Cách Vẽ Giao Tuyến Của Mặt Phẳng Với Khối Đa Diện -
Hình Chiếu Trục Đo Của Các Hình Song Song Với Mặt Xoz -
Ổ Đỡ Hình 6.6. Chia Ổ Đỡ Thành Các Phần -
Một Số Chú Ý Khi Ghi Kích Thước
Xem toàn bộ 116 trang tài liệu này.
4.2. Giao tuyến của các khối hình học
Các khối hình học tạo thành vật thể có thể có những vị trí tương đối khác nhau. Nếu hai khối hình học cắt nhau nghĩa là các mặt của hai khối hình học có những điểm chung, thì tập hợp tất cả những điểm chung đó là giao tuyến các mặt của hai khối hình học, thường gọi là giao tuyến vật thể.
Trong thực tế, thường gặp các giao tuyến có dạng khác nhau nên các mặt của vật thể hay của chi tiết máy.
Dưới đây sẽ xét cách vẽ giao tuyến của vật thể trong một số trường hợp đặc biệt thường gặp.
Những trường hợp đặc biệt là những trường hợp mặt của một hay hai vật thể là lăng trụ hay hình trụ, vuông góc với một hay hai mặt phẳng hình chiếu. Do đó hình chiếu của mặt vật thể trên mặt phẳng hình chiếu đó biến thành một đường, đường này cũng là hình chiếu của giao tuyến của hai vật thể trên mặt phẳng hình chiếu đó.
4.2.1. Giao tuyến của hai khối đa điện
4.2.1.1. Định nghĩa
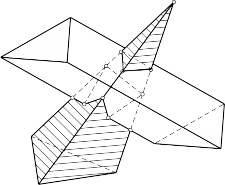
Giao của hai đa diện là một hay nhiều đường gẫy khúc. Mỗi cạnh của đường gẫy khúc là giao tuyến của hai mặt bên của hai đa diện. Mỗi đỉnh của đường gẫy khúc là giao điểm của một cạnh nào đó của một đa diện với đa diện còn lại (hình 4.9).
N ' S
6
M '
P' 5
7 8
2 1 4 N
3
A
P M
C
B
Hình 4.9. Giao tuyến của hai khối đa điện
4.2.1.2. Phương pháp vẽ giao của hai đa diện
Có hai phương pháp để xác định giao của hai đa diện.
- Phương pháp 1: Vẽ giao của từng mặt của một đa diện với đa diện còn lại.
- Phương pháp 2: Vẽ giao của từng cạnh của một đa diện với đa diện còn lại.
Nhận xét: Như vậy việc vẽ giao của hai đa diện quy về việc vẽ giao của mặt phẳng với đa diện (hay vẽ giao của đường thẳng với đa diện).
Chú ý: Khi nối hai đỉnh của giao chi được nối hai đỉnh bằng một đoạn thẳng khi hai đỉnh đó cùng thuộc hai mặt bên nào đó của hai đa diện.
Ví dụ:
Cho hình lăng trụ tứ giác giao với hình tháp. Hãy vẽ giao của hai khối hình học (hình 4.10)?
Ta chỉ cần vẽ giao của các mặt bện của hình lăng trụ với mặt hình chop. Ta vẽ giao của mặt bên BB’CC’ với mặt hình chóp. Mặt phẳng BB’CC’ cắt mặt hình chóp theo một tam giác 123. Vẽ giao của mặt AA’DD’ với chóp ta được đường gãy khúc 7456. Vẽ giao của mặt DD’CC’ với chóp ta được đường gãy khúc 687. Giao phải tìm gồm tam giác 123 và đường gãy khúc 456874 trên hình chiếu bằng.
Đường gẫy khúc kín 456874 khuất vì nó thuộc các mặt AA’DD’, DD’CC’ khuất trên hình chiếu bằng.
S1
B1 = B1'
A1 = A1'
41
11 21 31
C1 = C1'
51 81
61 = 71
D1 = D1'
42 | 72 | |||
82 | ||||
12 | S2 | 32 | ||
22 | 62 | |||
52 | ||||
A2 B2 | ||||
E1 F1 G1
A2'
B2' D2' C2'
E2
F2 D
2
G2
C2
Hình 4.10. Cách vẽ giao hai đa diện
4.2.2. Giao của đa diện với mặt cong
4.2.2.1. Định nghĩa
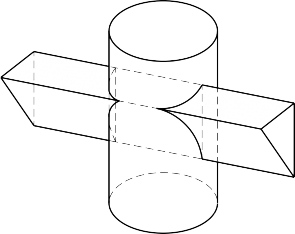
Giao tuyến của đa diện với mặt cong là tập hợp các giao tuyến của các mặt đa diện với mặt cong. Do vậy giao tuyến là đường khép kín của các cung cong hay các đoạn thẳng (hình 4.11).
m
n
p
Hình 4.11. Giao của đa diện với mặt cong
Trên hình 4.11 các mặt (m n), (n p) của lăng trụ cắt mặt trụ cho ta các cung elip; còn mặt (m p) của lăng trụ cắt mặt trụ cho ta các đoạn đường thẳng. Các đầu mút của các cung chính là các giao điểm của các cạnh đa diện với mặt cong.
4.2.2.2. Phương pháp vẽ giao tuyến
Vẽ giao tuyến của từng mặt của đa diện với mặt cong.
Chú ý: Để vẽ các cung cong cho chính xác ta cần tìm các điểm mút của các cung và các điểm đặc biệt của các cung đó.
Sau đây ta áp dụng phương pháp vẽ giao đa diện với một mặt cong qua ví dụ dưới đây.
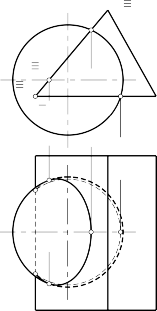
Ví dụ: Vẽ giao của lăng trụ chiếu đứng với mặt cầu (hình 4.12)?
B
B
'
1 1
61
41 51
21 31 O1
CC '
AA '
11 1 1
1 1
A
B
C
' ' '
2 2 2
42
22
62 12
32
52
A2 B2 C2
Hình 4.12. Cách vẽ giao của lăng trụ chiếu đứng với mặt cầu
Giải: Vì lăng trụ chiếu đứng cho nên giao tuyến có hình chiếu đứng thuộc đáy lăng trụ. Ta vẽ hình chiếu bằng của giao.
Mặt (AA’, BB’) cắt cầu theo giao tuyến là đường tròn trong không gian. Hình chiếu đứng là đoạn thẳng 21- 41- 61 đa biết. Hình chiếu bằng là elip. Để vẽ nó ta chú ý các điểm: 2, 3 là các đầu mút của elip; 4, 5 là các điểm chung của elip với đường bao hình chiếu bằng của cầu; điểm 6 thuộc đường tròn lớn mặt của cầu. Để vẽ hình chiếu bằng của các điểm đó ta gắn chúng vào các đường tròn bằng hay các đường tròn mặt của cầu.
Ta nối hình chiếu bằng 22-42-62-52-32 sao có dạng elip. Cung 4-6-5 thuộc nửa trên của cầu và mặt (AA’, BB’) thấy của lăng trụ trên hình chiếu bằng cho nên ta nối bằng nét liền cung 42-62-52. Cung 22-42, 32-52 nối bằng nét đứt, vì 2-4 và 3-5 thuộc nửa dưới của cầu.
Mặt (AA’, CC’) của lăng trụ song song với P2 cho nên cắt cầu theo đường tròn bằng. Hình chiếu đứng của giao đó là đoạn thẳng 11-21. Hình chiếu bằng là cung tròn 22-12-32.
4.2.3. Giao của hai mặt cong
4.2.3.1. Định nghĩa
Giao của hai mặt cong sẽ là một hay nhiều đường cong khép kín. Nếu hai mặt cong đại số có bậc là m và n thì giao tuyến của chúng là đường cong đại số bậc m.n.
Trên hình 4.13 mặt trụ bậc 2 (Ф2) cắt mặt nón bậc 2 (σ2) trường hợp này cho ta
giao tuyến là đường cong bậc 4.
Hình 4.13. Giao của mặt trụ với mặt nón
Để vẽ được giao tuyến của hai mặt cong ta phải tìm các điểm chung của hai mặt rồi nối lại. Do vậy ta phải tìm được các điểm đặc biệt tiếp xúc với các đường bao của hai mặt và càng nhiều điểm thì nối giao tuyến càng chính xác.
4.2.3.2. Ví dụ
Vẽ giao tuyến của mặt trụ chiếu đứng với mặt nón (hình 4.14)?
Giải: Giả thiết cho mặt trụ có đường sinh vuông góc với π2, cho nên giao tuyến nằm trên mặt trụ cũng có hình chiếu đứng thuộc đường tròn đáy trụ. Như vậy bài toán biết hình chiếu đứng của giao tuyến, ta chỉ còn tìm hình chiếu bằng của giao.
Để tìm các điểm của giao tuyến ta gắn các điểm đó vào đường sinh, hoặc các đường tròn song song với đáy nón. Ta chọn các điểm đặc biệt sau:
- Các điểm 2, 2’ là các điểm phải nhất, cũng thuộc đường sinh bao bên phải của hình chiếu bằng của trụ.
- Các điểm 3, 3’ là các điểm thấp nhất của giao tuyến (gần vòng tròn đáy nhất).
- Các điểm 1, 4 thuộc đường sinh bao bên trái trên hình chiếu đứng của nón.
S 1
11
71
61
21
51
2'
1
41
31 31
8
1
3 '
2
8 '
2
5'
2
7 '
2 '
2
2
6 '
42
12
2
72
62
2
2
52
32
82
Hình 4.14. Cách vẽ giao của mặt trụ chiếu đứng với mặt nón
Ngoài ra ta cần tìm thêm các điểm khác như là 5, 5’, 6, 6’, 8, 8’ để nối cho chính xác.
Như trên hình đã chỉ rò, để tìm hình chiếu bằng của các điểm nói trên, ta gắn chúng vào các đường sinh của nón, hoặc các đường tròn song song với đáy nón.
Trên hình chiếu bằng, cung 22-62-72-12-7’2-6’2-2’2 được nối bằng nét liền (thấy) vì thuộc nửa trên của trụ. Cung còn lại ở hình chiếu bằng được nối bằng nét đứt (khuất).
CÂU HỎI ÔN TẬP, BÀI TẬP
1. Giao tuyến giữa mặt phẳng với khối đa diện là gì? Khi vẽ cần phải tìm yếu tố giao tuyến nào?
2. Nói rò các trường hợp giao tuyến giữa mặt phẳng với hình trụ.
3. Giao tuyến giữa mặt phẳng với mặt cầu là gì? Cách tìm điểm thuộc giao tuyến
4. Giao tuyến của hai khối đa diện là gi? Cách xác định giao tuyến đó.
5. Giao tuyến của đa diện với mặt cong là gì? Cách xác định giao tuyến đó.
6. Giao tuyến của hai mặt cong là gì? Cách xác định giao tuyến đó.
15
Q1
Q1
3
Q1
10
4
60°
50
60
7. Cho mặt phẳng Q vuông góc mặt phẳng chiếu đứng cắt các khối hình học (hình 4.16). Hãy vẽ giao tuyến của chúng.
1
2
Ø50
Ø50
Ø60
Ø60
Q1
20
70
60
45°
Hình 4. 16
Ø30
Ø60
5
Q1
Q1
6
45°
45°
45
70
Hình 4.16 (tiếp)