Chương 5
HÌNH CHIẾU TRỤC ĐO
5.1. Khái niệm về hình chiếu trục đo
Các hình chiếu vuông góc thể hiện một cách chính xác hình dạng và kích thước của vật thể được biểu diễn, do đó trong kỹ thuật phương pháp các hình chiếu vuông góc được lấy làm phương pháp biểu diễn chính. Song mỗi hình chiếu vuông góc thường chỉ thể hiện được hai chiều của vật thể, nên hình vẽ thiếu tính lập thể, làm cho người đọc khó hình dung hình dạng của vật thể. Để khắc phục nhược điểm đó của phương pháp các hình chiếu vuông góc, người ta dùng phương pháp hình chiếu trục đo để bổ sung.
Hình chiếu trục đo thể hiện đồng thời trên một hình biểu diễn ba chiều của vật thể, nên hình vẽ có tính lập thể. Vì vậy, trên các bản vẽ của những vật thể phức tạp, bên cạnh các hình chiếu vuông góc, người ta thường còn vẽ thêm hình chiếu trục đo của vật thể đó.
Hình chiếu trục đo còn dùng để vẽ các sơ đồ, vẽ phác thảo các bộ phận trong giai đoạn thiết kế.
5.1.1. Nội dung phương pháp hình chiếu trục đo
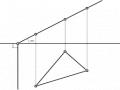
Lấy mặt phẳng P’ là mặt phẳng chiếu, phương chiếu l không song song với P’ và không song song với các trục tọa độ Ox, Oy, Oz (theo ba chiều dài, rộng, cao) của vật thể (hình 5.1). Chiếu vật thể cùng hệ tọa độ vuông góc theo phương chiếu l lên P’ ta được hình chiếu song song của vật thể, gọi là hình chiếu trục đo của vật thể.
P'
z
l
z'
C
O'
C'
O
A'
A
B'
B
x'
x
y'
y
Hình 5.1. Hình chiếu trục đo
- Các trục đo hình chiếu của ba trục tọa độ là các trục O’x’, O’y’ và O’z’.
- Góc trục đo là các góc
x'O ' y ', y 'O ' z ', x'O ' z '
- Tỉ số giữa độ dài hình chiếu của một đoạn thẳng nằm trên trục tọa độ với độ dài của đoạn thẳng đó gọi là hệ số biến dạng:
p = O'A'
OA
q =O'B'
OB
r =O'C'
OC
- hệ số biến dạng theo Ox;
- hệ số biến dạng theo Oy;
- hệ số biến dạng theo Oz.
5.1.2. Phân loại hình chiếu trục đo
Hình chiếu trục đo được phân loại theo phương chiếu l hay theo các hệ số biến dạng:
- Nếu phương chiếu l không vuông góc với mặt chiếu P’, ta có hình chiếu trục đo xiên góc ( l, P ' 900);
- Nếu phương chiếu l vuông góc với mặt chiếu P’, ta có hình chiếu trục đo vuông góc ( l, P ' 900);
- Nếu ba hệ số bằng nhau (p = q = r) ta có hình chiếu trục đo đều;
- Nếu hai trong ba hệ số biến dạng bằng nhau (ví dụ p = r ≠ q) ta có hình chiếu trục đo cân;
- Nếu ba hệ số biến dạng khác nhau (p ≠ q ≠ r) ta có hình chiếu trục đo lệch.
Trong vẽ kỹ thuật thường dùng loại hình chiếu trục đo xiên góc cân và loại hình chiếu trục đo vuông góc đều.
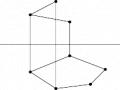
5.2. Hình chiếu trục đo vuông góc đều
5.2.1. Đặc điểm
z
P'
z'
O
y
O'
x'
y'
z'
120°
120°
x
x' 120° y'
p : q : r = 1 : 1 : 1
Hình 5.2. Hình chiếu trục đo vuông góc đều
- Các góc trục đo:
x'O ' y ' y 'O ' z ' x'O ' z ' 1200
(hình5.2)
- Hệ số biến dạng: p = q = r = 0,82
Để thuận tiện cho việc vẽ, người ta thường dùng hệ số biến dạng quy ước p = q = r = 1. Với hệ số biến dạng quy ước này, hình chiếu trục đo được xem như phóng to lên 1 : 0,82 = 1,22 lần so với thực tế.
5.2.2. Hình chiếu trục đo của các đường tròn
Hình chiếu trục đo của các đường tròn nằm trên các mặt song song với các mặt tọa độ là các elip có các trục dài vuông góc với các trục đo. Với hệ số biến dạng quy ước ta có:
Trục dài elíp bằng1,22d;
Trục ngắn elíp bằng 0,71d
(d là đường kính của đường tròn, hình 5.3).
0,71d
R
1
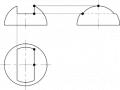
Hình chiếu trục đo vuông góc đều thường dùng để vẽ các vật mà các mặt đều có hình tròn. Khi vẽ có thể thay elíp bằng hình ôvan. Cách vẽ ôvan ngang xem hình 5.4.
O2 E F O3 O4 H G O1 | |
Hình 5.3. Hình chiếu trục đo vuông góc đều của các đường tròn | Hình 5.4. Cách vẽ ôvan thay elip |
Có thể bạn quan tâm!
-
Đường Thẳng Và Điểm Thuộc Mặt Phẳng -
Cách Vẽ Giao Tuyến Của Mặt Phẳng Với Khối Đa Diện -
Cách Vẽ Giao Của Lăng Trụ Chiếu Đứng Với Mặt Cầu -
Ổ Đỡ Hình 6.6. Chia Ổ Đỡ Thành Các Phần -
Một Số Chú Ý Khi Ghi Kích Thước -
Vẽ kỹ thuật - ĐH SPKT Nam Định - 13
Xem toàn bộ 116 trang tài liệu này.
d
- Trước hết xác định trục dài và trục ngắn của ôvan, vẽ hình thoi có cạnh bằng đường kính của đường tròn d, góc nhọn bằng 600, đường chéo dài của hình thoi trùng với trục dài của ôvan.
- Lấy các điểm giữa của các cạnh hình thoi E, F, G, H. Nối đỉnh O1 với E và F được các điểm giao O3 và O4.
- Lấy O1 làm tâm, bán kính R1 = O1E vẽ cung lớn và lấy O3 làm tâm, bán kính R = O3E vẽ cung bé. Sau đó vẽ các cung đối xứng có tâm O2 và O4 ta được hình ôvan.
Hình 5.5 là ví dụ về cách dựng hình chiếu trục đo vuông góc đều theo các hình chiếu vuông góc.
Z 1
X 1
X 2
Y 2
b) | |||||
c) | d) |
Hình 5.5. Cách vẽ hình chiếu trục đo vuông góc đều
5.3. Hình chiếu trục đo xiên góc cân
5.3.1. Đặc điểm
- Các góc trục đo:
x'O ' y ' y 'O ' z ' 1350
x'O ' z ' 900
(đặt mặt xOz // P’ như hình 5.6a);
- Hệ số biến dạng: p = r = 1 và q = 0,5
90°
45°
45°
90°
Trục O’z’ thể hiện chiều cao của vật thể được đặt thẳng đứng. Trục O’y’ làm với đường ngang O’x’ một góc 450 (hình 5.6b). Hình chiếu trục đo của các hình song song với mặt tọa độ xOz sẽ không biến dạng.
z' z' x' O' x' O' y' y' p : q : r = 1 : 1/2 : 1 | |
a) | b) |
Hình 5.6. Hình chiếu trục đo xiên góc cân
d
R
0,5d
1,06d
5.3.2. Hình chiếu trục đo của các đường tròn
C M B A O3 O N 7° D d O1 | |
Hình 5.7. Hình chiếu trục đo xiên góc cân của các đường tròn | Hình 5.8. Cách vẽ hình ô van thay cho elip trong HCTĐ xiên góc cân |
Hình chiếu trục đo của các đường tròn nằm trên các mặt song song với các mặt tọa độ xOy và yOz là các elíp (hình 5.7).
Trục dài elíp AB = 1,06d;
Trục ngắn elíp CD = 0,35d (d là đường kính đường tròn).
Khi vẽ, có thể thay e líp bằng hình ô van, cách vẽ xem hình 5.8:
- Vẽ đường tròn tâm O, đườn kính d và hướng trục dài AB làm với đường nằm ngang Ox’ một góc 70. Đường tròn cắt Ox’ tại M và N;
- Kẻ trục ngắn CD vuông góc với trục dài AB và lấy OO1 = d. Nối MO1, đường này cắt trục dài tại O3;
- Lấy O1 làm tâm, bán kính R = O1M vẽ cung lớn và lấy O3 làm tâm, bán kính r
= O3M vẽ cung nhỏ. Sau đó vẽ các cung đối xứng ta được hình ôvan.
5.3.3. Hình chiếu trục đo của các hình song song với mặt xOz
Hình chiếu trục đo của các hình song song với mặt xOz không biến dạng. Vì vậy nên đặt các mặt của vật thể có nhiều đường cong song song với mặt xOz.
Ví dụ, cách vẽ hình chiếu trục đo của vật thể theo các hình chiếu vuông góc cho trên hình 5.9.
Hình 5.9
Có thể lấy một mặt làm cơ sở để dựng hoặc vẽ hình hộp ngoại tiếp. Cách vẽ như hình 5.10.
Hình 5.10
5.4. Cách dựng hình chiếu trục đo
5.4.1. Các quy ước về hình chiếu trục đo
- Trong hình chiếu trục đo các thành mỏng , nan hoa,… vẫn vẽ ký hiệu vật liệu trên mặt cắt khi cắt dọc hay cắt ngang (hình 5.11).
Hình 5.11
- Trong hình chiếu trục đo cho phép vẽ riêng phần, phần không gian bị mặt phẳng cắt cắt qua được quy ước vẽ bằng các chấm nhỏ (hình 5.12).
Hình 5.12
- Cho phép vẽ ren, răng của các loại bánh răng theo quy ước như hình chiếu thẳng góc. Khi cần có thể vẽ hình chiếu trục đo của vài bước ren hay vài răng.
- Đường gạch gạch trong hình chiếu trục đo được kẻ song song với hình chiếu trục đo của đường chéo của hình vuông có các cạnh song song với trục toạ độ tương ứng.
40
20
30
26
16
Ø12
7
R10
20
7
- Khi ghi kích thước trên hình chiếu trục đo các yếu tố kích thước như đường gióng, đường kích thước, mũi tên, con số kích thước được kẻ và viết theo nguyên tắc biến dạng của hình chiếu trục đo (hình 5.13).
5.4.2. Chọn loại hình chiếu trục đo
Tuỳ theo hình dạng cấu tạo của từng vật thể và tuỳ theo mục đích thực hiện mà chọn loại hình chiếu trục đo cho thích hợp.
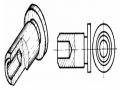
Ví dụ: để thể hiện khâu nối (hình 5.14) ta nên dùng loại hình chiếu trục đo vuông góc đều là tốt nhất. Hình chiếu trục đo này thể hiện rất rò các lỗ ở trên các mặt khác nhau (hình 5.15).
Hình 5.15 |
5.4.3. Dựng hình chiếu trục đo
* Phương pháp tọa độ: là phương pháp cơ bản dùng để dựng hình chiếu trục đo của vật thể.
Như ta đã biết, muốn dựng hình chiếu trục đo của một vật thể, ta phải biết cách dựng hình chiếu trục đo của một điểm. Cách dựng hình chiếu trục đo của một điểm như sau:
Trước hết phải vẽ các vị trí trục đo và xác định toạ độ vuông góc của điểm (XA, YA, ZA).
Z '
O
Y '
XA
Z '
A'
X
,
A x
,
Y '
, A2
A1
ZA
X
A
Ax
,
YA
Z A
X
Y
A
A 1
a) b)