đứng và hình chiếu cạnh là hai hình tam giác cân bằng nhau, có các cạnh bên thể hiện các đường sinh của hình nón. Cạnh đáy của tam giác cân thể hiện đường kính đáy của hình nón, chiều cao tam giác cân thể hiện chiều cao của hình nón (hình 3.54).
Muốn xác định một điểm K nằm trên mặt nón, vẽ qua K đường sinh của hình nón.
Hình 3.55 là các hình chiếu của hình nón cụt.
z
C1 D1
B1
D3
A3
B3
A1 C3
D
2
x y D B
B
A2 A C
2
C2 y
Hình 3.55. Hình chiếu của hình nón cụt
3.3.4.4. Hình cầu
z K3 K1 O1 O3 y x O O2 K2 y | |
Hình 3.56. Hình cầu | Hình 3.57. Hình chiếu của hình cầu |
Có thể bạn quan tâm!
-
Hình Chiếu Của Điểm, Đường Thẳng Và Mặt Phẳng -
Cách Vẽ Hình Chiếu Thứ Ba Từ Hai Hình Chiếu Của Điểm -
Đường Thẳng Và Điểm Thuộc Mặt Phẳng -
Cách Vẽ Giao Của Lăng Trụ Chiếu Đứng Với Mặt Cầu -
Hình Chiếu Trục Đo Của Các Hình Song Song Với Mặt Xoz -
Ổ Đỡ Hình 6.6. Chia Ổ Đỡ Thành Các Phần
Xem toàn bộ 116 trang tài liệu này.
Hình cầu là hình tròn xay được tạo thành bởi một nửa hình tròn quay xung quanh đường kính. Nửa đường tròn tạo thành dạng mặt cầu, đường kính là trục quay (hình 3.56).
Các hình chiếu vuông góc của hình cầu đều là các hình tròn bằng nhau, có đường kính bằng đường kính của hình cầu (hình 3.57).
Muốn xác định một điểm K thuộc mặt cầu, vẽ qua K đường tròn song song với mặt chiếu.
3.4. Kích thước của các khối hình học
Hình chiếu thể hiện hình dạng của vật thể còn kích thước thể hiện độ lớn của vật thể.
Khối hình học cơ bản có hình dạng đơn giản nên thường được thể hiện bằng hai hình chiếu. Độ lớn của các khối hình học cơ bản thường được thể hiện bằng các kích thước: chiều dài, chiều rộng và chiều cao (xem bảng 3.1).
Khối hình học
Khối hình học
2. Hình trụ
3. Hình lăng trụ lục giác
đều
4. Hình nón
1. Hình hộp chữ nhật
5. Hình chóp đều
Ød
Ød
h
h
h
h
h
b
Bảng 3.1
a
b | |
a |
6. Hình cầu
cÇu Ød
CÂU HỎI ÔN TẬP, BÀI TẬP
1. Thế nào là phép chiếu xuyên tâm, phép chiếu song song và phép chiếu thẳng góc?
2. Nêu cách xây dựng hình chiếu của điểm và các tính chất của các hình chiếu của điểm.
3. Nêu cách vẽ hình chiếu thứ ba từ hai hình chiếu.
4. Nêu cách chuyển từ tọa độ Đề các sang đồ thức của điểm.
5. Nêu điều kiện để điểm thuộc đường thẳng? Biểu diễn dưới dạng đồ thức.
6. Thế nào là vết của đường thẳng. Tính chất vết của đường thẳng.
7. Nêu điều kiện để đường thẳng và điểm thuộc mặt phẳng.
8. Thế nào là vết của mặt phẳng. Tính chất vết của mặt phẳng.
9. Muốn vẽ hình chiếu của một khối đa diện, ta vẽ hình chiếu của những yếu tố hình học nào (lấy ví dụ)?
10. Làm thế nào để xác định một điểm nằm trên mặt của một khối đa diện (lấy ví dụ)?
11. Mặt tròn xoay được tạo thành như thế nào? Hãy vẽ hình chiếu của hình trụ, hình nón và hình cầu.
12. Làm thế nào để xác định một điểm nằm trên mặt tròn xoay (lấy ví dụ)?
13. Vẽ hình chiếu cạnh của điểm A (hình 3.58)
x A 2 A1 b) |
Hình 3.61. Hình bài tập 15
14. Cho ngũ giác phẳng ABCDE, hãy vẽ hình chiếu đứng C1 và D1 của C và D (hình 3.59)?
B 1
A1
E 1
x
E 2
D2
A2
B 2 C 2
Hình 3.59. Hình bài tập 14
15. Tìm hình chiếu còn lại của B và C biết ABC là mặt phẳng mặt (hình3.60)
16. Tìm hình chiếu còn lại của B và C biết ABC là mặt phẳng bằng (hình 3.61)
A 1 x A2 C 2 B2 Hình 3.61. Hình bài tập 16 |
B 1
17. Tìm vết của mặt phẳng P được xác định bởi hai đường thẳng a, b biết:
a. a // b (hình 3.62a)
b. a×b (hình 3.62b)
a 1 b1 x a 2 b2 | |
a) | b) |
Hình 3.62. Hình bài tập 17
18. Vẽ hình chiếu d1của đường thẳng d biết rằng d thuộc mặt phẳng (ABC) (hình 3.63).
B 1
A 1
x
A 2
d2
B 2
C 1
C 2
Hình 3.63. Hình bài tập 18
19. Cho hai hình chiếu của các khối hình học (hình 3.64).
a. Hãy vẽ hình chiếu thứ ba.
b. Biết các điểm A, B, C… nằm trên mặt của các khối hình học và một hình chiếu của chúng, hãy tìm hai hình chiếu của các điểm.
A2 | B2 | z O y | y | 2 x | C1 D2 | z O y | y | ||
3 | z | 4 | z | ||||||
E1 | (I1) | ||||||||
F1 | H1 | ||||||||
x | O | y | x | O | y | ||||
G2 | |||||||||
y | y | ||||||||
5 | z | 6 | z | ||||||
U3 | |||||||||
M1 | |||||||||
(J1) | P1 | Q3 | |||||||
x | O | y | x | O | y | ||||
N2 | |||||||||
K2 | |||||||||
y | y |
1
Hình 3.64. Hình bài tập 19
Chương 4
GIAO TUYẾN CỦA VẬT THỂ
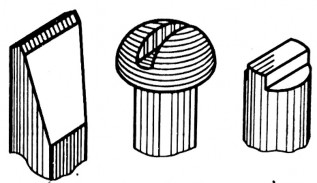
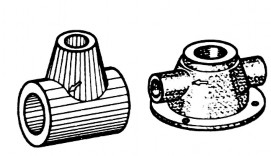
Trong thực tế, ta thường gặp một số vật thể (hay chi tiết máy) được cấu tạo bởi các khối hình học không hoàn toàn, nghĩa là các khối hình học bị các mặt phẳng cắt đi một phần, như lưỡi đục (hình4.1a) là hình lăng trụ bị vát phẳng; đầu vít (hình 4.1b) là hình chỏm cầu bị các mặt phẳng cắt thành rãnh; đầu trục (hình 4.1c) là hình trụ bị các mặt phẳng cắt hai bên. Chúng ta cũng thường thấy các khối hình học tạo thành vật thể (hay chi tiết máy) có vị trí tương đối khác nhau làm thành các giao tuyến khác nhau giữa các bề mặt của vật thể như ống nối, nắp máy (hình 4.2) có giao tuyến của hình trụ và hình nón.
| |
a) b) c) | a) b) |
Hình 4.1. Lưỡi đục, đầu vít và đầu trục | Hình 4.2. Ống nối và nắp máy |
Để vẽ hình dạng của vật thể (hay chi tiết máy), phải giải các bài toán về giao tuyến của vật thể. Sau đây xét cách vẽ giao tuyến của mặt phẳng với khối hình học và giao tuyến của hai khối hình học trong một số trường hợp thường gặp.
4.1. Giao tuyến của mặt phẳng với khối hình học
Mặt phẳng cắt khối hình học tạo thành mặt cắt, đường bao mặt cắt đó gọi là giao tuyến của mặt phẳng với khối hình học. Vẽ phần bị cắt của vật thể, thực chất là vẽ giao tuyến của mặt phẳng với khối hình học của vật thể đó.
4.1.1. Giao tuyến của mặt phẳng với khối đa diện
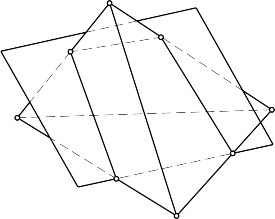
Giao của một mặt phẳng với một đa diện là một đa giác phẳng. Mỗi cạnh của giao là giao tuyến của mặt phẳng cắt với mặt bên của đa diện và mỗi đỉnh của giao là giao điểm của một cạnh đa diện với mặt phẳng cắt (hình 4.3).
Để tìm giao, ta có hai phương pháp:
- Phương pháp 1- tìm đỉnh của giao: tìm mỗi đỉnh của giao bằng cách giải bài toán tìm giao điểm của một cạnh đa diện với mặt phẳng cắt.
- Phương pháp 2- tìm cạnh của giao: tìm mỗi cạnh của giao bằng cách giải bài toán tìm giao của mặt phẳng cắt với một mặt bên của đa diện.
A
4 3
B D 2
1
C
Hình 4.3. Giao tuyến của mặt phẳng với khối đa diện
Vậy để giải quyết bài toán tìm giao của mặt phẳng với đa diện, ta thực hiện theo nội dung sau:
1- Tìm đầy đủ các đỉnh của giao tuyến: sử dụng phương pháp 2 ở trên.
2- Nối các đỉnh của giao tuyến: để nối hai đỉnh lại với nhau ta phải xét xem 2 đỉnh đó có cùng thuộc một mặt bên của đa diện không. Nếu có thì nối hai đỉnh với nhau thành 1 cạnh của giao tuyến.
3- Vẽ thấy, khuất: sau khi tìm được giao thì ta xét thấy, khuất cho các cạnh của giao.
Ví dụ:
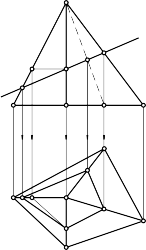
Vẽ giao của mặt phẳng chiếu đứng α với hình chóp S.ABCD (hình 4.4).
S1
31
21
11 41
A1 B1 D1 C1 D
A2 12
42
S232
C
22 2
B2
Hình 4.4. Cách vẽ giao tuyến của mặt phẳng với khối đa diện
Vì α P1 cho nên đường gấp khúc giao tuyến có hình chiếu đứng dễ dàng xác định được. Và các đỉnh của đường gấp khúc là:
11 = S1A1 x α1
21 = S1B1 x α1
31 = S1C1 x α1
41 = S1D1 x α1
Từ đó dóng xuống hình chiếu bằng ta có: 12, 22, 32, 42. Đường gấp khúc giao tuyến nối theo thứ tự: 1-2-3-4-1. Hình chiếu bằng 1222324212 được nối bằng đường thấy.
4.1.2. Giao tuyến của mặt phẳng với hình trụ
Tùy theo vị trí của mặt phẳng đối với trục của hình trụ, để có các giao tuyến sau:
- Nếu mặt phẳng song song với trục của hình trụ thì giao tuyến là một hình chữ nhật (hình 4.5a).
- Nếu mặt phẳng vuông góc với trục của hình trụ thì giao tuyến là một hình tròn (hình 4.5b).
- Nếu mặt phẳng nghiêng với trục của hình trụ thì giao tuyến là một hình elip (hình 4.5c).
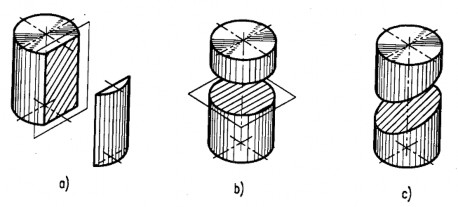
Hình 4.5. Giao tuyến của mặt phẳng với hình trụ
A1 B1
A3
B3
A2 B2
Hình 4.6. Hình chiếu của rãnh ở đầu trục