Đường Thẳng Và Điểm Thuộc Mặt Phẳng

B

ma m

1

B

P1 A1

1

A1 C1

A2

C1 A Bx

n

B 2

na C

C 2

P2

Hình 3.33 Hình 3.34

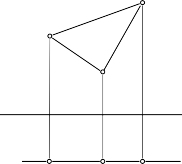
Tính chất:

- Hình chiếu đứng của mặt phẳng (ABC) suy biến thành một đường thẳng trùng với vết đứng mα (hình 3.34).

- Vết bằng của mặt phẳng (ABC) vuông góc với trục x: nα x.

- Góc nghiêng: (mα, x) = (α, P2)

b. Mặt phẳng chiếu bằng

Mặt phẳng chiếu bằng là mặt phẳng vuông góc với mặt phẳng hình chiếu bằng P2: β P2 (hình 3.35).

Tính chất:

- Hình chiếu bằng của mặt phẳng β suy biến thành một đường thẳng trùng với vết bằng mβ (hình 3.37).

- Và vết đứng của mặt phẳng β vuông góc với trục x: nβ x.

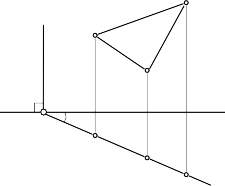
- Góc nghiêng: (nβ, x) = (β, P1).

P1

m C

B

A

b

B 2 A

2 C 2 n

P2

B1 C1 m A1 x b C2 A2 B 2 n
Hình 3.35	Hình 3.36

Có thể bạn quan tâm!

• Chia Đường Tròn Thành 5 Phần Và 10 Phần Bằng Nhau
• Hình Chiếu Của Điểm, Đường Thẳng Và Mặt Phẳng
• Cách Vẽ Hình Chiếu Thứ Ba Từ Hai Hình Chiếu Của Điểm
• Cách Vẽ Giao Tuyến Của Mặt Phẳng Với Khối Đa Diện
• Cách Vẽ Giao Của Lăng Trụ Chiếu Đứng Với Mặt Cầu
• Hình Chiếu Trục Đo Của Các Hình Song Song Với Mặt Xoz

Xem toàn bộ 116 trang tài liệu này.

c. Mặt phẳng chiếu cạnh

Mặt phẳng chiếu cạnh là mặt phẳng vuông góc với mặt phẳng hình chiếu cạnh P3: γ P3 (hình 3.37).

P1 m

B B 3

A A3 P 3

x

C C3

y

P 2 n

m z B1 B3 A1 A 3 C 3 x C1 n
Hình 3.37	Hình 3.38

z

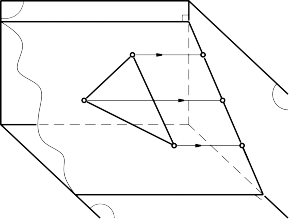
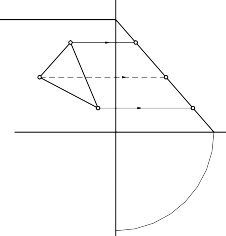
Tính chất

- Hình chiếu cạnh của mặt phẳng suy biến thành một đường thẳng trùng với vết cạnh của nó.

- Vết đứng và vết bằng song song với trục x (hình 3.38).

- Góc hợp bởi hình chiếu cạnh và trục z là góc hợp bởi mặt phẳng

γ và P1.

γ và P2.

- Góc hợp bởi hình chiếu cạnh và trục y là góc hợp bởi mặt phẳng

d. Mặt phẳng mặt

Mặt phẳng mặt là mặt phẳng song song với mặt phẳng hình chiếu đứng P1: α // P1 (hình 3.39).

P1 C1

B1

A1

C

B

A

B 2 A2 C 2 n

P2

B1 C1 A1 x n C2 A2 B 2
Hình 3.39	Hình 3.40

Tính chất

- Vết bằng song song với trục x: nα // x (hình 3.40).

- Mọi điểm của α có hình chiếu bằng thuộc nα

- Hình chiếu đứng của tam giác A1B1C1 nằm trong α bằng tam giác ABC thực.

e. Mặt phẳng bằng

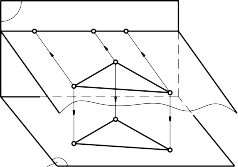
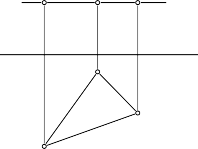
Mặt phẳng bằng là mặt phẳng song song với mặt phẳng hình chiếu bằng P2: β // P2 (hình 3.41).

P1

C1 A1 B1 m

A

C B A2

C 2 B 2

P2

C1 A1 B1 m x A2 B 2 C 2
Hình 3.41	Hình 3.42

Tính chất:

- Vết đứng song song với trục x: mβ // x (hình 3.42)

- Mọi điểm của β có hình chiếu đứng thuộc mβ

- Hình chiếu bằng của tam giác A2B2C2 nằm trong mặt phẳng β bằng tam giác ABC thực.

e. Mặt phẳng cạnh

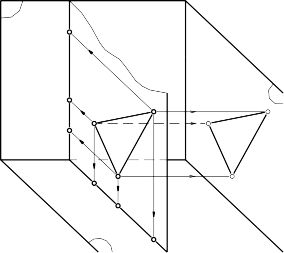
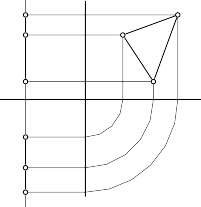
Mặt phẳng cạnh là mặt phẳng song song với mặt phẳng hình chiếu cạnh P3: γ // P3 (hình 3.43).

P1

C1 z

A1 C P 3

A

B A C3

1 3

x

A B B3

2

B2

y

P 2 C2

m z C1 A C3 A3 1 B1 B3 x A2 B2 C2 n
Hình 3.43	Hình 3.44

Tính chất

- Vết đứng và vết bằng của mặt phẳng cạnh đều vuông góc với trục x. Mọi điểm thuộc mặt phẳng cạnh có hình chiếu đứng thuộc vết đứng, và hình chiếu bằng thuộc vết bằng của mặt phẳng.

A1B1C1 mγ (hình 3.44) A2B2C2 nγ

- Hình chiếu cạnh của tam giác A3B3C3 thuộc mặt phẳng cạnh thì bằng tam giác ABC thực.

3.2.4.4. Đường thẳng và điểm thuộc mặt phẳng

Điều kiện để một đường thẳng thuộc mặt phẳng là đường thẳng đó đi qua 2 điểm của mặt phẳng.

Điều kiện để một điểm thuộc mặt phẳng là điểm đó thuộc một đường thẳng của mặt phẳng.

Ví dụ:

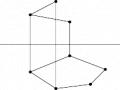
Cho đồ thức của mặt phẳng α(a x b). Hãy xác định hình chiếu còn lại của đường thẳng g biết g α (hình 3.45)

Nhận thấy do g nằm trong mặt phẳng α mà:

g1 x a1 = 11 và g1 x b1 = 21

Dóng từ 11 xuống a2 ta có 12; dóng từ 21 xuống b2 ta có 22. Nối 12 và 22 ta được g2

O1

a1

g

21

1

1

b

1

1

x

g

1 2 2 b2

a 22 2

O2

Hình 3.45

3.3. Hình chiếu của các khối hình học

Một vật thể thường được cấu tạo từ những khối hình học cơ bản như hình lăng trụ, hình chóp, hình trụ, hình nón, hình cầu …

Sau đây là hình chiếu của các khối hình học thường gặp

3.3.1. Khối hình chữ nhật

Để cho đơn giản, dễ vẽ, ta đặt đáy ABCD song song với mặt phẳng hình chiếu bằng P2, mặt bên ABB’A’ song song với mặt phẳng hình chiếu cạnh P3. Sau đó vẽ hình chiếu của các đỉnh của hình hộp trên ba mặt phẳng hình chiếu. Các hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh là các hình chữ nhật thể hiện hình dạng thật của các mặt hình hộp. Một hình chiếu thể hiện được hai chiều của hình hộp chữ nhật (hình 3.46).

z

K

C

B

C 3

K1 K3

A3

D1

B1

C1

D3

A1 B3

C 2

x y

D2

D

A2 A

K2 B 2

y

Hình 3.46. Hình chiếu của khối hình hộp

Muốn xác định điểm K nằm trên mặt của hình hộp, vẽ qua K đường thẳng nằm trên mặt của hình hộp.

3.3.2. Hình lăng trụ đều

Đặt mặt đáy của lăng trụ đều song song với mặt phẳng chiếu bằng, sẽ có hình chiếu bằng thể hiện hình dạng thật của mặt đáy, hình chiếu đứng và hình chiếu cạnh thể hiện chiều cao của hình lăng trụ (hình 3.47).

z

C

B1

C1

A3

C 3

A1 B 3

C 2

x y

A2

A B

B 2

y

Hình 3.47. Hình chiếu của khối hình lăng trụ

3.3.3. Hình chóp đều và hình chóp cụt đều

3.3.3.1. Hình chóp đều

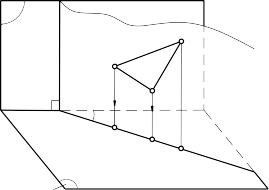
Đặt đáy của hình chóp đều song song với mặt chiếu bằng, sẽ có hình chiếu bằng thể hiện hình dạng thật của mặt đáy; hình chiếu đứng và hình chiếu cạnh thể hiện chiều cao của hình chóp (hình 3.48).

Muốn xác định một điểm K thuộc mặt của hình chóp đều, vẽ qua K đường thẳng nằm trên mặt của hình chóp đều.

S1 z S3

F

E

B

C

S

K1 K3

B1

E1

D1

E3

F3 A3

D3

B3

A1

F1 C1 C3

F2

E2

x y AD

K

D

A2 S2

2 2

B 2 C2

y

Hình 3.48. Hình chiếu của hình chóp

3.3.3.2. Hình chóp cụt đều

z

x y

y

Hình 3.49. Hình chiếu của hình chóp cụt

Cách vẽ hình chiếu và cách xác định điểm nừm trên mặt của hình chóp cụt, tương tự như trường hợp hình chóp. Hình 3.49 là hình chiếu của hình chóp cụt đều có đáy là một hình vuông đặt song song với mặt phẳng hình chiếu bằng và các cạnh của hình vuông đặt song song với mặt phẳng hình chiếu đứng và mặt phẳng hình chiếu cạnh.

3.3.4. Khối tròn

3.3.4.1. Khái niệm

Khối tròn là khối hình học giới hạn bởi mặt tròn xoay hay giới hạn bởi một phần mặt tròn xoay và mặt phẳng.

Mặt tròn xoay là mặt tạo bởi một đường bất kì, được quay một vòng quanh một đường thẳng cố định. Đường bất kì đó gọi là đường sinh của mặt tròn xoay; đường thẳng cố định gọi là trục quay của mặt tròn xoay. Mỗi điểm của đường sinh khi quay, sẽ tạo thành mọt đường tròn có tâm nằm trên trục quay và bán kính bằng khoảng cách từ điểm đó đến trục quay (hình 3.50).

a)

b)

c)

Hình 3.50. Các khối tròn

- Nếu đường sinh là đường thẳng song song với trục quay, sẽ tạo thành mặt trụ tròn xoay (hình 3.50a).

- Nếu đường sinh là đường thẳng cắt trục quay, sẽ tạo thành mặt nón tròn xoay (hình 3.50b).

- Nếu đường sinh là nửa đường tròn, quay quanh trục là đường kính của nửa đường tròn đó thì sẽ tạo thành mặt cầu (hình 3.50c).

Để xác định một điểm nằm trên một mặt tròn xoay, phải dựng qua điểm đó một đường sinh hay một đường tròn của mặt tròn xoay đó.

3.3.4.2. Hình trụ

Hình trụ là khối tròn xoay được tạo thành bởi một hình chữ nhật quay quanh một cạnh của nó. Cạnh song song với trục quay là đường sinh tạo thành mặt xung quanh của hình trụ và hai cạnh kia của hình chữ nhật tạo thành hai mặt đáy của hình trụ (hình 3.51).

Để hình vẽ đơn giản, đặt mặt đáy của hình trụ song song với mặt phẳng chiếu bằng, sẽ có hình chiếu bằng thể hiện hình dạng thật của đáy. Hình chiếu đứng và hình chiếu bằng là hai hình chữ nhật bằng nhau, một cạnh của hình chữ nhật này thể hiện chiều cao của hình trụ và cạnh kia thể hiện đường kính đáy (hình 3.52).

K

D B

A C

z K1 K3 A1 C1 D1 B1 D3 A B3 C3 3 y x D2 A2 B 2 K2 C 2 y
Hình 3.51. Hình trụ	Hình 3.52. Hình chiếu của hình trụ

Muốn xác định một điểm K nằm trên mặt trụ, vẽ qua K đường sinh của hình trụ.

3.3.4.3. Hình nón

Hình nón là khối tròn xoay, được tạo thành bởi một tam giác vuông quay quanh một cạnh của góc vuông, đường huyền là đường sinh tạo thành mặt xung quanh của hình nón, còn cạnh góc vuông còn lại tạo thành đáy hình nón (hình 3.53).

S

K

D B

A C

z S1 S3 K1 K 3 C3 A1 C1 D1 B1 D3 A3 B3 y x D2 A2S2 B 2 K2 C2 y
Hình 3.53. Hình nón	Hình 3.54. Hình chiếu của hình nón

Để hình vẽ đơn giản, đặt đáy hình nón song song với mặt phẳng hình chiếu bằng, thu được hình chiếu bằng thể hiện hình dạng thật của đáy hình nón. Hình chiếu