Định Lý Oxtrogratxki – Gauss Đối Với Từ Trường

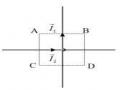
Từ đó ta có:

I

Idl sinI 2



B 0

0sin.d

2

4dd r

4R

1

0 I (cos4R1

1

Vectơ cường độ từ trường:

 cos2 )

Chú ý:

H  4R

(cos1

 cos2 )

(3.11)

Trường hợp dây dẫn dài vô hạn thì 1  0; 2 

khi đó:

Bài toán 2:

B o I ;

M 2R

HM 

I

2R

(3.12)

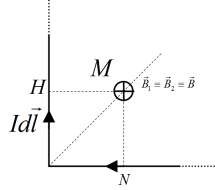
Xác định vectơ cảm ứng từ gây ra bởi một dòng điện thẳng dài vô hạn được uốn thành một góc vuông, tại điểm M nằm trên đường phân giác của góc vuông.

Định hướng:

Ta có thể vận dụng bài toán 1 để tìm vectơ cảm ứng từ hoặc vectơ cường độ từ trường do dây dẫn thẳng gây ra tại một điểm M nào đó. Trước hết cần xem xét dòng điện thẳng dài vô hạn hay hữu hạn để lựa chọn

công thức phù hợp. Trong bài toán này, để thỏa mãn điều kiện dây dẫn thẳng thì ta phải chia dây dẫn dài vô hạn thành hai đoạn dây thẳng dài hữu hạn.

Giải:

Chia dòng điện thành hai dòng điện thẳng.

Khi đó theo nguyên lý chồng chất từ trường:

B B1 B2

Dựa vào kết quả của bài toán trên ta có:

Gốc	Phương	Chiều	Độ lớn
B1	M	mp dây dẫn	hình vẽ	B 0 I (cos cos) 1 4.MN 1 2
B2	M	mp dây dẫn	hình vẽ	B 0 I (cos'  cos' ) 2 4.MH 1 2

Có thể bạn quan tâm!

• Điều Kiện Cân Bằng Tĩnh Điện. Tính Chất Của Vật Dẫn Mang Điện
• Năng Lượng Tương Tác Của Một Hệ Điện Tích Điểm
• Định Luật Amper Về Tương Tác Giữa Hai Phần Tử Dòng Điện
• Tác Dụng Của Từ Trường Lên Một Phần Tử Dòng Điện
• Lực Từ Tác Dụng Lên Hạt Mang Điện Chuyển Động
• K Sẽ Có Dấu Dương Nếu Nó Có Chiều Sao Cho Đường Cảm Ứng Từ Do

Xem toàn bộ 258 trang tài liệu này.

Ở đây:

0

1  0 , 2  135 ,

'  450 , '  1800 .

lớn:

1

Vì B1 và

2

B2 là hai vectơ cùng phương chiều nên tổng vectơ thành tổng độ

B B1 B2

B 0 I

4.HM

(cos 0  cos1350 ) 

0 I

4.HM

(cos 45o  cos1800 )

Bài toán 3:

B 0 I

4.HM

(2  2 ) (T )

Một dòng điện có cường độ I chạy trong dây dẫn mảnh được uốn thành vòng tròn bán kính R. Xác định cảm ứng từ gây ra bởi dòng điện tại một điểm M nằm trên trục của nó và cách tâm O đường tròn một khoảng h.

Giải:

Ta chia dòng điện thành các phần tử dòng điện từ gây ra bởi phần tử này tại M có:

Idl , khi đó ta có cảm ứng

 Độ lớn: dB 0

4

Idl sin, ở đây sin1 vì I dl vuông góc với r

r2

 Phương vuông góc với mặt phẳng chứa

Idl

và r (tức là nằm trong

mặt phẳng chứa OM và r ), có chiều xác định theo qui tắc vặn nút chai.

Vì cảm ứng từ do các phần tử Idl khác nhau trên đường tròn gây ra tại M có phương và chiều khác nhau vì thế tích phân vectơ không thể chuyển thành tích phân đại số mà ta sử dụng tính đối xứng của hình tròn.

Xét hai phần tử dòng điện

Idl1

và Idl2 có cùng độ lớn đặt đối xứng nhau

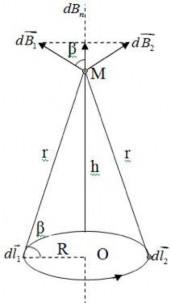
qua tâm O, ta thấy vectơ cảm ứng từ do chúng gây ra tại M lần lượt là dB1 và dB2 nằm trên cùng một đường thẳng đối xứng nhau qua trục của đường tròn (trục OM) và có giá trị như nhau, do đó vectơ cảm

ứng từ tổng hợp dB1 dB2 có phương OM. Vì vậy, vectơ cảm ứng từ toàn phần do dòng điện tròn gây ra tại M là vectơ có phương trùng với trục OM.

Như vậy cảm ứng từ toàn phần do dòng điện tròn gây ra tại M được tính theo công thức:

B 

( AB)

dBn

trong đó Bn là hình chiếu của dB lên OM.

Nếu gọi β là góc giữa OM và

dB thì ta có:

Hình 3.4. Cảm ứng từ của dòng điện tròn

B dB cos 

0 Idl R 0 IR

.2R



dd dd

4r2 r 4r3



I (R 2 )

B0

2r3

B 

0 IS

2(R2 h2 )3 / 2

Cường độ từ trường:

H IS

(3.13)

2(R2 h2 )3 / 2

Cho h=0 ta tìm được biểu thức của vectơ cảm ứng từ gây bởi dòng điện tại tâm O của dòng điện.

Bài toán 4:

H IS

2R3

(3.14)

Một dòng điện có cường độ I chạy trong dây dẫn mảnh được uốn thành cung tròn bán kính R. Xác định cảm ứng từ gây ra bởi dòng điện tại tâm O của cung tròn.

Giải:

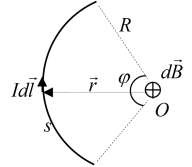
Ta chia dòng điện thành các phần tử dòng điện Idl , khi đó cảm ứng từ gây ra tại O:

dB có:



dB 

0

4

Idl 

r

r3

 Gốc tại O

 Phương vuông góc với mặt phẳng dây dẫn (mặt phẳng chứa r và O)

 Chiều xác định theo qui tắc vặn nút chai như hình vẽ

 Độ lớn:

dB 0

4

Idl sin

r2

Theo nguyên lý chồng chất từ trường ta có:

B dB

dd

Vì các vectơ dB do các phần tử dòng điện của dây sinh ra đều cùng phương chiều nên tích phân vectơ có thể chuyển thành tích phân đại số:

B 

dd

dB 0 I

4

dl sin



r

2

dd

Ta có sin1 vì I dl vuông góc với r và

r R

không đổi, nên:

I s

0

B dB 2 dl

dd 4R 0

B 0 I.s

4R2

Mặt khác s R

B 0 I R0 I

(3.15)

4R2

Cường độ từ trường:

H I.sI

4R

(3.16)

4R2 4R

Từ đó, ta có thể tìm được cảm ứng từ và cường độ từ trường tại tâm vòng dây ứng với dòng điện tròn: s  2R và  2.

B 0 I.2

4R

0 I

2R

(3.17)

H 0 I

2R

I

2R

(3.18)

3.3. TỪ THÔNG. ĐỊNH LÝ O-G ĐỐI VỚI TỪ TRƯỜNG

3.3.1. Đường cảm ứng từ

Trong một từ trường bất kì, vectơ cảm ứng từ có thể biến đổi từ điểm này qua điểm khác cả về phương chiều và độ lớn.

Vì vậy, để có hình ảnh cụ thể trực quan về sự biến đổi ấy người ta đưa ra khái niệm đường cảm ứng từ.

Đường cảm ứng từ là đường cong mà tiếp tuyến tại mọi điểm của nó trùng với phương của vectơ cảm ứng từ tại những điểm ấy, chiều của đường cảm ứng từ là chiều của vectơ cảm ứng từ.

Các đường cảm ứng từ không cắt nhau và là các đường cong khép kín.

Quy ước, vẽ số đường sức xuyên qua một đơn vị diện tích đặt vuông góc với phương của vectơ cảm ứng từ tại điểm xét tỉ lệ với độ lớn của vectơ B tại

điểm đó. Gọi d

là số đường sức qua diện tích

dSn

đặt vuông góc với vectơ

B thì ta có dBdSn

Ý nghĩa của đường cảm ứng từ: là hình ảnh khái quát cụ thể để biểu diễn từ trường (biểu diễn từ trường về phương diện hình học).

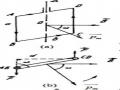
Tập hợp các đường cảm ứng từ gọi là từ phổ.

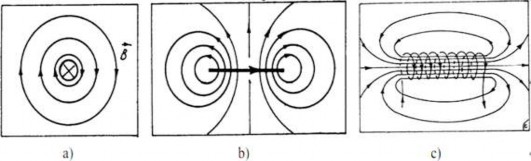
Hình 2.5. Từ phổ của: a. Dòng điện thẳng

b. Dòng điện tròn

c. Ống dây điện

Từ trường đều là từ trường trong đó vectơ B có phương chiều và độ lớn như nhau tại mọi điểm trong từ trường. Như vậy, các đường cảm ứng từ của từ trường đều là các đường song song và cách đều nhau.

3.3.2. Từ thông

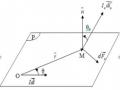
Xét diện tích S đặt trong một từ trường đều B thì thông lượng của vectơ cảm ứng từ B gửi qua diện tích S ( goi tắt là từ thông kí hiệu ) là một đại lượng có trị số tỉ lệ với số đường sức từ gửi qua mặt đó xác định bởi công thức:

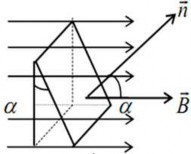
Hình 3.6. Từ thông gửi qua diện tích phẳng

B.S B.S.cos(3.19)

trong đó S S.n với n là vectơ pháp tuyến của mặt phẳng S

hợp bởi giữa n và B .

và α là góc

Nếu S vuông góc với các đường cảm ứng từ mà ta qui ước vẽ sao cho

số đường cảm ứng từ xuyên qua một đơn vị diện tích đúng bằng B thì 

biết số đường cảm ứng từ xuyên qua S .

cho

Từ thông qua một mặt hữu hạn S đặt trong từ trường: ta phải chia mặt S

thành các phần tử diện tích nhỏ dS sao cho trên dS từ trường có thể coi là đều.

Khi đó từ thông qua dS sẽ là:

dB.dS

Từ thông qua mặt S là:

B. dS

S

(3.20)

Đơn vị từ thông: trong hệ SI đơn vị của từ thông là Vêbe (kí hiệu: Wb). Từ công thức:

[B][]Wb T (Tesla)

[S] m2

Vậy Tesla: Tesla là cảm ứng từ của một từ trường đều cho từ thông một vêbe gửi qua diện tích một mét vuông đặt vuông góc với đường cảm ứng từ.

3.3.3. Tính chất xoáy của từ trường

Các đường sức từ là các đường cong khép kín. Mà chúng ta đã biết, một trường có các đường sức là những đường cong khép kín gọi là trường xoáy. Vậy từ trường là một trường xoáy hay từ trường có tính chất xoáy.

3.3.4. Định lý Oxtrogratxki – Gauss đối với từ trường

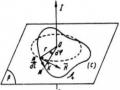
Xét một mặt kín S bất kì trong từ trường. Trên mặt S có các đường các đường cảm ứng từ đi vào và đi ra khỏi mặt. Quy ước vẽ trên mặt kín pháp tuyến dương hướng ra ngoài. Khi đó từ thông do những đường cảm ứng đi vào mặt có dấu âm, và đi ra mặt thì có dấu dương. Mặt khác, các đường cảm ứng từ là khép kín nên có bao nhiêu đường đi vào thì cũng có bấy nhiêu đường đi ra khỏi mặt S. Nên từ thông do các đường cảm ứng từ đi vào và đi ra khỏi mặt S là bằng nhau nhưng trái dấu thì từ thông gửi qua một mặt kín phải bằng không. Từ đó ta có định lý Oxtrogratxki – Gauss đối với từ trường:

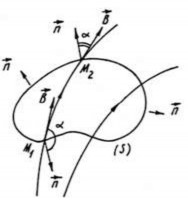
Từ thông gửi qua một mặt kín bất kì bằng

không.

B.dS  0

S

(3.21)

Dạng vi phân của định lý Oxtrogratxki – Gauss đối với từ trường:

divB  0





(3.22) Hình 3.7



B B B  0

x y z

Xem tất cả 258 trang.