Các Thành Tố Về Năng Lực Tính Toán Của Chương Ii Giải Tích 12

B. Yêu cầu về kỹ năng cần đạt được

Biết dùng các tính chất của lǜy thừa để đơn giản biểu thức, so sánh những biểu thức có chứa lǜy thừa.

Biết vận dụng tính chất của các hàm số mǜ, hàm số lôgarit vào việc so sánh hai số, hai biểu thức chứa mǜ và logarit; biết vẽ đồ thị các hàm số lǜy thừa, hàm số mǜ, hàm số lôgarit; tính được đạo hàm các hàm số đó.

Giải được một số phương trình, bất phương trình mǜ đơn giản bằng các phương pháp đưa về lǜy thừa cùng cơ số, lôgarit hóa, dùng ẩn phụ, sử dụng tính chất của hàm số; giải được một số phương trình, bất phương trình lôgarit đơn giản hoặc phức tạp bằng các phương pháp đưa về lôgarit cùng cơ số, mǜ hóa hoặc ứng dụng máy tính để giải các bài toán trắc nghiệm.

C. Yêu cầu về tư duy và thái độ cần đạt được

Rèn luyện tính cẩn thận, chính xác. Tư duy các vấn đề toán học một cách lôgit và hệ thống.

1.2.2. Các thành tố về năng lực tính toán của chương II giải tích 12

Từ những biểu hiện của năng lực toán học và năng lực tính toán; Căn cứ vào nội dung chương II Giải tích 12 chúng tôi có thể rút ra một số thành tố của năng lực tính toán cụ thể như sau:

A. Năng lực nhận biết công thức, đồ thị, tính chất

Có thể bạn quan tâm!

• Phát triển năng lực tính toán cho học sinh trong dạy học bài tập hàm số lũy thừa, hàm số mũ và hàm số logarit giải tích 12 trung học phổ thông - 1
• Phát triển năng lực tính toán cho học sinh trong dạy học bài tập hàm số lũy thừa, hàm số mũ và hàm số logarit giải tích 12 trung học phổ thông - 2
• Những Thành Tố Của Nltt Trong Chủ Đề Hàm Lǜy Thừa, Hàm Số Mǜ Và Hàm Số Logarit
• Thực Trạng Dạy Học Phát Triển Năng Lực Tính Toán Chương Ii Hàm Số Lǜy Thừa, Hàm Số Mǜ Và Hàm Số Lôgarit Cho Học Sinh Ở Một Số Trường Phổ Thông
• Các Biện Pháp Phát Triển Năng Lực Tính Toán Cho Học Sinh Thông Qua Hoạt Động Dạy Bài Tập Hàm Số Lǜy Thừa, Hàm Số Mǜ Và Hàm Số Logarit
• Biện Pháp 2: Rèn Luyệncho Học Sinh Biết Sử Dụng Máy Tính Cầm Tay Để Kiểm Tra Lại Đáp Số

Xem toàn bộ 140 trang tài liệu này.

Theo khung đánh giá năng lực 6 bậc của Bloom thì:“ Nhận biết là khả năng ghi nhớ và nhận diện thông tin. Nhớ là cần thiết cho tất các mức độ tư duy. Nhớ ở đây được hiểu là nhớ lại những kiến thức đã học một cách máy móc và nhắc lại”.

Mức độ này là mức độ nhận biết học sinh cần nắm được công thức, tính chất cơ bản của hàm số lǜy thừa, hàm số mǜ và hàm số logarit để nhận dạng được các dạng bài tập cơ bản. Đầu tiên học sinh phải nắm được một số công thức cơ bản sau đây:

 man a m

a

a

a

c

log a

b

a

 log b  logcb

log a

a

1

 log b 

 log  log b  log c

a c a a



b



b

 

b

a

 

 a



a

a

a

a



a

 log b  1 log b

 a 

a

a

 log b  log b

a

 a.a a 



a

an

1. Các công thức cơ bản

 an  1

 alogab b ;

 (ab) a.b

 log (b.c)  log b  log c

 (am)n am.n  (an)m

Đổi cơ số

n

Đạo hàm

( xn)’ = n.xn-1

( ex )’ = ex

( ax)’ = ax.lna

 ( un)’ = n.un-1.u’

 ( eu )’ = eu .u’

 ( au)’ = au.lna.u’

( log x )’ =

1

x.ln a

 ( log u )’ =

1 .u '

u.ln a

2. Tập xác định của hàm lǜy thừa: y = u

+  nguyên dương ( Z +) => u thuộc R

+  nguyên âm hoặc bằng 0 => u khác 0

+  không nguyên => u > 0

3. Hàm số mǜ : y = ax

+ TXĐ : D = R

; y = log x

+ Hàm số đồng biến khi a > 1. Hàm số nghịch biến khi 0 < a < 1

4. Hàm số logarit: y = loga x

+ TXĐ: x > 0

+ Hàm số đồng biến khi a > 1. Hàm số nghịch biến khi 0 < a < 1

5. PT Mǜ

Cách 1:Cùng cơ số : ax =b = ay <=> x = y

Cách 2:Không cùng cơ số :ax =b <=> x = log b

a

Cách 3: Đặt ẩn phụ:A.a2x +b.ax +C = 0 Đặt t  ax ; t >0, giải tìm t => x

6. Phương trình logarit: ( logax : Đk: 0  a  1 và x > 0 ) Cách 1: Cùng cơ số : loga x  b  loga y <=> x = y

Cách 2: Không cùng cơ số : loga x  b <=> x = a

b

Cách 3: Đặt ẩn phụ: A. log2x  B.log x  C  0

a

a

Đặt t  log x ; Giải tìm t => x

a

7. Bất pt mǜ và logarit

Chú ý: + Cơ số a >1 : không đổi chiều

+ Cơ số 0< a <1 : đổi chiều

8. Lãi suất kép : A  a(1  r)n

Ví dụ 1.3. Chọn khẳng định đúng. Với M, N dương khi đó

log3 (M .N )  ?

A. log3M  log3N B. log3M  log3N

C. log3(M  N ) D. log3M .log3N

Việc nhớ công thức cơ bản học sinh dễ tìm được đáp án là B

Ví dụ 1.4. Chọn khẳng định đúng. Đạo hàm của hàm số

y  2x là:

A. x.2x1

B. 2x.lnx

C. 2x.ln 2

D. 2x.ln 3

Việc nhớ công thức cơ bản của đạo hàm ax' ax.ln a

tìm được đáp án là C.

Ví dụ 1.5. Đồ thị này là của hàm số nào?

học sinh dễ

y

4

3

2

1

x

-4 -3 -2 -1

1 2 3 4

 1x

A. y   

 2 

B. y  2x

 1x

C. y   

 3 

D. y  3x

x2 x 12

Trong câu này học sinh chỉ cần nhận biết hàm số tăng là a >1. Do đồ thị đi qua ( 1; 3) nên ta chọn đáp án D.

Ví dụ 1.6. Tập xác định của hàm số

y  log3

là:

A. D  4;3

C. D  R 4

B. D  ; 4  3; 

D. D  4;3

Học sinh chỉ cần đặt điều kiện

x2 x  12  0

ta chọn được đáp án B.

B. Năng lực biến đổi các công thức, tính chất cơ bản

Theo thang đánh giá 6 bậc của Bloom thì học sinh biến đổi được công thức, tính chất chính là mức độ hiểu.

Hiểu là khả năng hiểu, diễn dịch, diễn giải, giải thích hoặc suy diễn (dự đoán được kết quả hoặc hậu quả). Hiểu không đơn thuần là nhắc lại cái gì đó. HS phải có khả năng diễn đạt khái niệm theo ý hiểu của mình.

Ví dụ 1.7. Cho log

a b  3, loga

c  5 . Khi đó log

b

bc c

bằng

A.  5

3

B. 5 3

C. 1 4

D.  1

4

Giải:

Học sinh dùng công thức, tính chất tìm được:

b  a3 ,

c  a5

sau đó thế vào log

b

bc c

Sau đó biến đổi bằng những phép biến đổ cơ bản Kết quả chọn D

a 3 a

3 b2

Ví dụ 1.8. Rút gọn dưới dạng lǜy thừa của là

2

 b

A. a3

 

3

 b

B.  a2

 

C. a b

D. b a

Giải: Học sinh dùng công thức, tính chất của lǜy thừa, rút gọn Chọn được kết quả là A.

C. Năng lực sử dụng máy tính để tìm đáp án của câu hỏi trắc nghiệm trong chương II Giải tích 12

Năng lực sử dụng máy tính cầm tay biểu hiện của năng lực này là khả năng tìm hiểu thêm các thủ thuật bấm máy tính cầm tay nhằm tìm được đáp án chính xác cho mỗi câu hỏi trắc nghiệm khách quan.

Ví dụ 1.9. Cho log9x = log12 y = log16 (x + y). Giá trị của tỉ số x là

y

1  5

A. B. 5 1

2 2

Giải

C. 1 D. 2

Từ log9x = log12y  y  12log9x.

Thay vào log9x = log16(x + y) ta được: log9x  log16 x  12log9x 0

Ta có thể dò được nghiệm của phương trình này bằng chức năng ấn phím SHIFT SOLVE

Lưu nghiệm này vào biến A

Từ giá trị của x ta suy ra giá trị của y  12log9x. Lưu giá trị y vào biến B

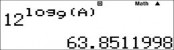
Đến đây ta dễ dàng tính được tỉ số x  A

y B

Đây chính là giá trị 5 1 và đáp án chính xác là B.

2

Ví dụ 1.10. Tập nghiệm của:

2log3 4x 3 log1 2x 3  2

3

A. 3 ;3

B. 3 ;  C. 3 ;3

D.  3 ;  

 4 

 4   4   4 

   

Ta nhận thấy khó khăn hơn nếu thuần túy giải bằng tay theo phương pháp tự luận. Sau đây là hướng dẫn cách sử dụng máy tính

Nhập vào máy tính:

2 log3(4x  3)  log1(2x  3)  2

3

CALC

3

=

Nếu được kết quả âm ta nhận. Sau đó CALC vài số nữa nhỏ hơn 3 và lớn hơn 0,75 cǜng được kết quả âm. Vậy đáp án là C.

D. Năng lực phát hiện, khám phá để giải quyết vấn đề liên quan đến hàm số lǜy thừa, hàm số mǜ, hàm số lôgarit

Theo từ điển Tiếng Việt [20]: Khám phá là tìm ra, phát hiện ra cái còn giấu, cái bí mật.

Khám phá là thuật ngữ dùng chủ yếu trong dạy học các môn khoa học trong nhà trường. Nó đề cập đến cách đặt câu hỏi, cách tìm kiếm tri thức hoặc thông tin, tìm hiểu về các hiện tượng.

Theo tác giả Bùi Văn Nghị thì khám phá là quá trình hoạt động và tư duy có thể bao gồm: quan sát, phân tích, nhận định, đánh giá, nêu giả thuyết, suy luận… nhằm đưa ra các khái niệm, phát hiện ra những tính chất, quy luật… trong sự vật hiện tượng và mối liên hệ giữa chúng.

Trong nội dung chủ để, năng lực khám phá thể hiện ở chỗ: Sử dụng được máy tính cầm tay, phần mềm, phương tiện công nghệ, nguồn tài nguyên trên mạng Internet để giải quyết một số vấn đề toán học. Chúng tôi chủ yếu khai thác các yếu tố giải bài tập toán, từ các bài đơn giản làm tiền đề để giải các bài phức tạp hơn. Cǜng từ đó chúng tôi khám phá các bài toán thực tiễn về lãi suất, các bài toán tìm m, các bài toán trong sinh học, vật lý.

Ví dụ 1.11. Khám phá cách giải bào toán : 25x 6.5x 5  0

Định hướng cách giải bài toán:

Bước 1: Biến đổi 25x về mǜ với cơ số 5.

Bước 2: Đặt ẩn phụ t  5x ,t  0 ta được phương trình bậc hai theo t.

Bước 3: Giải phương trình theo t và so sánh với điều kiện. Bước 4: Giải phương trình mǜ cơ bản.

Sau đó giáo viên có thể cho học sinh giải các bài tập ở bài tập 2 để nâng dần mức độ khó khăn của dạng toán này.

Ví dụ 1.12. Giải các phương trình sau:

2 2

a) 72x 1  8.7x 1  0 b) 9x x1 10.3x x2  1  0

* Từ các ví dụ trên giáo viên có thể định hướng cho học sinh khám phá bài toán tổng quát sau:

Bài toán: Xét phương trình

m, n, p  R

m.a2f ( x )  n.a f( x )  p  0

với 0  a  1 và

Bước 1: Đặt ẩn phụ t  a f( x ) ,t  0 . Khi đó ta có: m.t2 n.t  p  0 . Bước 2: Giải phương trình theo t và so sánh với điều kiện của t.

Bước 3: Đưa về phương trình mǜ cơ bản và ta giải phương trình tìm x

E. Năng lực sử dụng công cụ, phương tiện

Công cụ, hương tiện dạy học có vai trò chủ yếu như sau:

- Có thể cung cấp cho học sinh các kiến thức một cách chắc chắn và chính xác, như vậy nguồn tin họ thu nhận được trở nên đáng tin cậy và được nhớ lâu bền hơn.

- Làm cho việc giảng dạy trở nên cụ thể hơn. Vì vậy tăng thêm khả năng của học sinh tiếp thu những sự vật, hiện tượng và các quá trình phức tạp mà bình thường học sinh khó nắmvững được.

- Rút ngắn thời gian giảng dạy mà việc lĩnh hội kiến thức của học sinh lại nhanh hơn.

- Giải phóng người thầy giáo một khối lượng lớn các công việc tay chân, do đó làm tăng khả năng nâng cao chất lượng dạy học.

- Dễ dàng gây được cảm tình và sự chú ý của học sinh.

- Bằng việc sử dụng phương tiện dạy học, giáo viên có thể kiểm tra một cách khách quan khả năng tiếp thụ kiến thức cǜng như hình thành kĩ năng, kĩ xảo của học sinh.

- Năng lực sử dụng công cụ, phương tiện trong dạy chương Hàm số lǜy thừa, hàm số mǜ và hàm số logarit thể hiện một hệ thống nhiều cách giải toán, cách nào tối ưu nhất, cách nào nhanh nhất và chính xác nhất, điều đó học sinh và giáo viên phải có kiến thức tổng hợp tốt khi đó việc chọn lựa mới hiệu quả.

Ví dụ 1.13. Giải bất phương trình: logx(2x2 – 7x +5) > 1

A. T   4

;5   4

;  

B. T   ; 4

  4

;  

 6

 6

 6

 6

 2 2   2   2   2 

       

Xem tất cả 140 trang.