Phát triển kiến thức và thực hành nghiệp vụ của giáo viên Toán tương lai để dạy học thống kê

Bài 3. ĐỘ PHÂN TÁN CỦA DỮ LIỆU TRÊN BIỂU ĐỒ CỘT VÀ BIỂU ĐỒ HISTOGRAM

I. MỤC TIÊU

Qua bài này giúp học sinh:

+ Nhận biết được thế nào là độ phân tán của dữ liệu.

+ Dựa vào biểu đồ cột và biểu đồ histogram, so sánh độ phân tán của các dữ liệu.

- Nhắc lại khái niệm và ý nghĩa của phương sai và độ lệch chuẩn. Từ đó, dựa vào giá trị của phương sai, độ lệch chuẩn để xác định độ phân tán của dữ liệu.

- Học sinh xác định được độ phân tán của dữ liệu thông qua các dạng biểu đồ cột và biểu đồ histogram.

2. Kĩ năng:

- Biết cách áp dụng giá trị của phương sai, độ lệch chuẩn để phân tích độ phân tán của dữ liệu.

- Học sinh hình thành được kĩ năng đọc biểu đồ, xác định độ phân tán của dữ liệu thông qua hình dạng biểu đồ.

3. Thái độ:

- Nghiêm túc, tích cực, chủ động, độc lập và hợp tác trong các hoạt động nhóm.

- Say sưa, hứng thú trong học tập và tìm tòi nghiên cứu liên hệ thực tiễn.

4. Năng lực, phẩm chất:

- Năng lực: Năng lực giải quyết vấn đề, năng lực hợp tác, năng lực tự học, năng lực ứng dụng kiến thức toán vào cuộc sống

- Phẩm chất: Tự tin, tự lập.

II. CHUẨN BỊ.

1. Gv: Phấn màu, slides trình chiếu.

2. Hs: Ôn tập kiến thức: Số trung bình, số trung vị, mốt.

III. TỔ CHỨC CÁC HOẠT ĐỘNG DẠY HỌC

Hoạt động của GV

Hoạt động của HS

Nội dung

Hoạt động 1: Nhắc lại kiến thức

- Mục tiêu: Nhắc lại và củng cố kiến thức về các chỉ số thống kê như: Phương sai, độ lệch chuẩn.

- Phương thức hoạt động: Cá nhân.

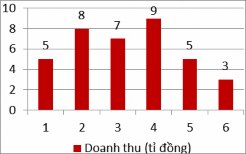
Bài toán: Dựa vào biểu đồ hãy tính phương sai và độ lệch chuẩn của mẫu dữ liệu.

GV. Trước khi thực hiện yêu cầu bài toán, các em dựa vào kiến thức lớp 10, hãy nêu công thức tính phương sai, độ lệch chuẩn.

GV. Nhắc lại công thức phương sai, độ lệch chuẩn.

GV. Để tính phương sai, độ lệch chuẩn chúng ta cần xác định các giá trị xi , số các giá trị N và số trung bình cộng của tổng thể.

GV. Mời 1 HS nêu các giá trị.

HS. Thực hiện yêu cầu

HS.

TH1: HS nêu được công thức.

TH2. HS không nhớ kiến thức.

HS.

1. Nhắc lại kiến thức

Bài toán: Dựa vào biểu đồ biểu diễn doanh thu 6 tháng đầu năm của một công ty, hãy tính phương sai và độ lệch chuẩn của mẫu dữ liệu.

- Phương sai là trung bình cộng của bình phương độ lệch của các giá trị số với trung bình của tổng thể.

n .(x x )2 n .(x x )2

s2 1 1 k k

f .(x x )2 f .(x x )2

1 1 k k

Trong đó: ni , fi lần lượt là tần số, tần suất của giá trị xi ; N là số các số liệu thống kê; x là số trung bình

của mẫu số liệu đã cho.

- Độ lệch chuẩn là căn bậc hai của phương sai.

Có thể bạn quan tâm!

Xem toàn bộ 277 trang tài liệu này.

GV. Vậy bây giờ chúng ta sẽ tiến hành tính số trung bình cộng của tổng thể.

GV. Mời một bạn nêu công thức tính số trung bình của tổng thể.

GV. Nhắc lại công thức tính số trung bình cộng của tổng thể.

H. Dựa vào công thức, các em hãy tính và nêu kết quả của số trung bình cộng của tổng thể.

Ở đây, chúng ta chỉ có 6 giá trị nên không cần phải lập bảng tần số mà các em chỉ cần cộng tất cả các giá trị lại và chia cho số các giá trị.

GV. Đã có số trung bình cộng của tổng thể, các giá trị và số các giá trị. Dựa vào

công thức các em hãy

1. (Nhầm với tháng) Các giá trị là: 1; 2; 3; 4; 5; 6.

2. (Đúng) Các giá trị là: 5; 8; 7; 9; 5; 3.

Đ. Số các giá trị là 6.

HS.

1. Nêu được công thức.

2. HS không nhớ công thức.

Đ. x  6,17

HS.

S 2  4, 97

S S 2  2, 23

Đ.

s s2

- Giải

Các giá trị là: 5; 8; 7; 9; 5; 3.

N  6

CT tính số trung bình của tổng thể.

x x1.n1 x2 .n2  ... xn .xn

x  5  8  7  9  5  3  6,17

(5  6,17)2  (8  6,17)2  (7  6,17)2

2 (9  6,17)2  (5  6,17)2  (3  6,17)2

S 

 4, 97

S S 2  2, 23

- Ý nghĩa của phương sai, độ lệchchuẩn:

Phương sai s2 và độ lệch chuẩn s đều được dùng để đánh giá mức độ phân tán của các số liệu thống kê (so với số trung bình cộng).

H. Từ đây chúng ta có thể suy ra số các giá trị là bao nhiêu?

H. Phương sai và độ lệch chuẩn dùng để làm gì?

GV. Đây cũng chính là ý nghĩa của phương sai và độ lệch.

HS1. Không nhớ. HS2. Phương sai s2 và độ lệch chuẩn s đều được dùng để đánh giá mức độ phân tán của các số liệu thống kê (so với

số trung bình cộng).

Hoạt động 2: Hình thành kiến thức, luyện tập

- Mục tiêu: Giúp học sinh biết thế nào là độ phân tán của một dữ liệu và cách để ước lượng độ phân tán của một dữ liệu.

- Phương thức hoạt động: Cá nhân

GV. Phương sai, độ lệch chuẩn được dùng để đánh giá mức độ phân tán (độ biến thiên) của dữ liệu. Vậy, độ phân tán (độ biến thiên) của dữ liệu là gì, và làm thế

nào để chúng ta ước lượng nó trên biểu đồ. Chúng ta sẽ cùng tìm hiểu.

GV. Giới thiệu độ phân tán (độ biến thiên) của dữ liệu.

H. Độ phân tán (độ biến thiên) của dữ liệu được so sánh thông qua những giá trị nào?

H. Theo các em, độ phân tán (độ biến

Đ.

HS1. (Nhầm khoảng giá trị) Độ phân tán (độ biến thiên) được so sánh thông qua khoảng cách giữa GTLN và GTNN

của dữ liệu.

HS2. (Đúng) Độ phân tán (độ biến thiên) được so sánh thông qua phương sai và độ lệch chuẩn.

Đ.

HS1. Em không

2. Thế nào là độ phân tán (độ biến thiên) của một mẫu dữ liệu?

- Độ phân tán là một thuật ngữ thống kê được đo bằng phương sai và độ lệch chuẩn.

- Chú ý: Giá trị phương sai, độ lệch chuẩn càng lớn thì độ phân tán càng cao và ngược lại.

tính phương sai và độ lệch chuẩn.

GV. Nêu chú ý.

biết.

HS2. Phương sai, độ lệch chuẩn càng lớn thì độ phân tán (độ biến thiên) càng bé.

HS3. Không có sự phụ thuộc giữa các chỉ số và độ phân tán (độ biến thiên).

HS4. Giá trị của phương sai, độ lệch chuẩn càng lớn thì độ phân tán (độ biến

thiên) càng cao.

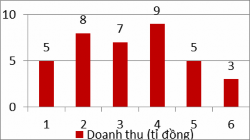
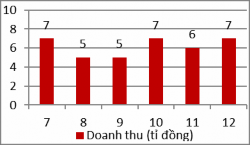
GV. Để xác định, so sánh độ phân tán của dữ liệu, ngoài việc sử dụng tính toán phương sai và độ lệch chuẩn, chúng ta còn có thể thực hiện việc ước lượng, so sánh bằng cách dựa vào biểu đồ.

Ví dụ 1: GV.

1. Các em hãy đưa ra dự đoán so sánh về độ phân tán của dữ liệu được cho ở hai biểu đồ trên.

Ví dụ 1:

1. Dự đoán

HS1. Độ phân tán của biểu đồ 2 cao hơn biểu đồ 1 vì các cột giá trị ở biểu đồ 2 đồng đều hơn.

HS2. Độ phân tán của hai biểu đồ là như nhau vì tổng doanh thu của 6 tháng đầu và cuối

năm đều là 37.

3. So sánh độ phân tán của dữ liệu dựa trên biểu đồ.

Ví dụ 1: Hai biểu đồ sau đây biểu diễn doanh thu của một công ty trong năm 2019.

Biểu đồ 1. Doanh thu 6 tháng đầu năm.

Biểu đồ 2. Doanh thu 6 tháng cuối năm.

thiên) phụ thuộc như thế nào vào giá trị của phương sai, độ lệch chuẩn?

2. Bây giờ, các em hãy sử dụng công thức tính phương sai, độ lệch chuẩn để kiểm tra dự đoán của mình.

GV. Qua tính toán phương sai và độ lệch chuẩn, thì ta thấy dự đoán độ phân tán của biểu đồ 1 cao hơn biểu đồ 2 là đúng.

GV. Đó là cách so sánh độ phân tán của dữ liệu thông qua tính toán phương sai và độ lệch chuẩn. Tuy nhiên, các em chú ý rằng phương sai và độ lệch chuẩn chính là trung bình cộng của độ lệch dữ liệu so với số trung bình cộng.

HS3. Độ phân tán của biểu đồ 1 cao hơn biểu đồ 2 vì độ chênh lệch giữa các cột cao hơn.

HS4. Từ biểu đồ không thể đưa ra dự đoán.

Biểu đồ 1.

S 2  4,97; S  2, 23

Biểu đồ 2.

S 2  0,97; S  0,98

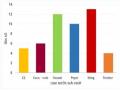
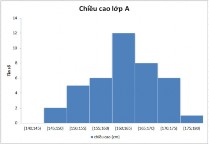
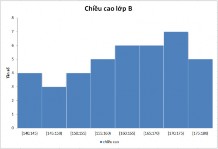
1. Các em hãy đưa ra dự đoán so sánh về độ phân tán của dữ liệu được cho ở hai biểu đồ trên.

2. Tính phương sai, độ lệch chuẩn ở mỗi biểu đồ.

Giải:

2. Biểu đồ 1. S 2  4,97; S  2, 23

Biểu đồ 2. S 2  0,97; S  0,98

- Nhận xét: Doanh thu của 6 tháng đầu năm có độ phân tán cao hơn.

Ví dụ 2: Hai biểu đồ dưới đây biểu diễn chiều cao của 40 học sinh lớp A và lớp B. Chiều cao của học sinh lớp nào có độ phân tán cao hơn? Vì sao?

Mức độ chênh lệch càng lớn thì độ phân tán càng lớn và ngược lại.

Ví dụ 2:

H. Các em hãy dự đoán chiều cao của lớp nào có độ phân tán cao hơn? Vì sao?

Ví dụ 2: Đ.

HS1. Chiều cao lớp A có độ phân tán cao hơn vì cột cao nhất có giá trị là 12 còn biểu đồ chiều cao lớp B có cột cao nhất là 7.

HS2. Chiều cao lớp B có độ phân tán cao hơn vì các dữ liệu trên biểu đồ trải dài hơn.

- Giải:

Chiều cao lớp A ít biến thiên hơn lớp B vì ở biểu đồ chiều cao lớp A, dữ liệu tập trung ở gần giá trị trung bình nhiều hơn; còn ở biểu đồ chiều cao lớp B, dữ liệu tản đều 2 bên, cách xa giá trị giá trị trung bình hơn.

Như vậy, ngoài cách sử dụng phương sai, độ lệch chuẩn, ta còn có thể so sánh độ phân tán của dữ liệu thông qua biểu đồ dựa vào mức độ chênh lệch giữa chiều cao các cột so với giá trị trung bình.

H. Như đã biết, ta cần phải có giá trị trung bình cộng để so sánh độ phân tán của dữ liệu. Vậy để xem dự đoán nào đúng, đầu tiên các em hãy ước lượng giá trị trung bình ở 2 biểu đồ đã cho.

GV. Ta thấy 2 biểu đồ tương đối đối xứng nhau, nên giá trị trung bình sẽ xấp xỉ trung vị (chia biểu đồ thành 2 phần diện tích bằng nhau) nên giá trị trung bình sẽ nằm trong khoảng 160 – 165 cm.

Giờ đây, chúng ta thấy các giá trị ở biểu đồ chiều cao lớp A những cột ở trung tâm cao nên có nhiều giá trị gần với giá trị trung bình. Suy ra độ phân tán nhỏ. Còn ở biểu đồ chiều cao lớp

B, các cột giá trị tản

HS3. Chiều cao lớp A có độ phân tán cao hơn vì độ chênh lệch chiều cao các cột so với giá trị trung bình (khoảng 5

- 6) lớn hơn.

Đ.

HS1. (Nhầm sang cột tần số)

- Biểu đồ chiều cao lớp A: khoảng 5 – 6.

- Biểu đồ chiều cao lớp B: 5

HS2. (Dựa vào số lượng các cột)

- Biểu đồ chiều cao lớp A: khoảng 160 – 165 cm.

- Biểu đồ chiều cao lớp B: 160cm

HS3. (chính xác)

- Cả 2 biểu đồ đều nằm trong khoảng 160 – 165cm.

GV. Đưa ra nhận xét, dự đoán của HS2 là đúng nhưng phần giải thích chưa hoàn toàn chính xác.

GV. Các em hãy chú ý đến hình dạng của biểu đồ histogram, ở biểu đồ chiều cao học sinh lớp A có dạng hình chữ V úp sẽ có

độ phân tán thấp.

Hoạt động 3: Luyện tập, củng cố

- Mục tiêu: Giúp học sinh vận dụng các kiến thức vừa tiếp cận vào giải một số bài tập.

- Phương thức hoạt động: Cá nhân

Bài tập trắc nghiệm.

Câu 1. Hai biểu đồ dưới đây biểu diễn lượng mưa hàng tháng của hai vùng A và

B. Lượng mưa vùng nào có độ phân tán lớn hơn?

A. Lượng mưa vùng A phân tán cao hơn vùng B.

B. Lượng mưa vùng B phân tán cao hơn vùng A.