Nhà máy đóng mới và sửa chữa tàu thủy

Tiếp bảng VI-8.

Hàm

c/H	j - i
c/H	9	10	11	12	13	14	15	16	17
(1)	(2)	(3)	(4)	(5)	(6)	(7)	(8)	(9)	(10)	(11)
	0	-7.780	-7.991	-8.181	-8.355	-8.517	-8.664	-8.802	-8.931	-9.052
	1/32	-7.699	-7.891	-8.062	-8.214	-	-	-	-	-
F	1/16	-7.451	-7.621	-7.743	-7.844	-	-	-	-	-
	1/2	-	-	-	-	-	-	-	-	-
	1	-	-	-	-	-	-	-	-	-
	2	-	-	-	-	-	-	-	-	-
	4	-	-	-	-	-	-	-	-	-
	0	0.0249	0.0202	0.0166	0.0140	0.0119	0.0102	0.0089	0.0078	0.0069
	1/32	0.0267	0.0219	0.0183	-	-	-	-	-	-
	1/16 1/2 1	0.0298 - -	0.0244 - -	0.0203 - -	- - -	- - -	- - -	- - -	- - -	- - -
	2	-	-	-	-	-	-	-	-	-
	4	-	-	-	-	-	-	-	-	-
	0	0.0019	0.0013	0.0009	0.0006	0.0004	0.0003	0.0002	0.0002	0.0002
	1/32	0.0020	0.0012	-	-	-	-	-	-	-
	1/16 1/2 1	0.0019 - -	0.0013 - -	- - -	- - -	- - -	- - -	- - -	- - -	- - -
	2	-	-	-	-	-	-	-	-	-
	4	-	-	-	-	-	-	-	-	-

Có thể bạn quan tâm!

Xem toàn bộ 232 trang tài liệu này.

http://www.ebook.edu.vn 157

K i 

1 .

b.i

(VI-14)

Hệ số độ mềm của gối ở góc k trên hướng ngang phải xét đến tính đàn hồi của đáy

được tính theo công thức sau: Kk 

b.k

 E. F

(VI-15)



Hàm độ lún đối với lớp đàn hồi chịu nén được xác định theo bảng VI-8, trong đó có

các ký hiệu sau: Fi j  Fn = i - j ;

i j n = i - j ;

i j

n = i - j

Các hàm độ lún n và n được xác định theo công thức sau:

n  Fn-1  2. Fn  Fn + 1 ; n = n - 1  2.n n + 1. (VI-16)

Các hàm độ lún đối với lớp chịu nén ΔFijk và Δijk được xác định theo công thức

ΔFi j k

 Fi j  Fi k ;

Δi j k 

i j i k

. (VI-16)

Các giá trị của hàm ΔFijk được cho trong bảng VI-9.

Khi tính toán khung trên nền đàn hồi có khoảng cách khác nhau giữa các gối trong phạm

vi tường và đáy cần phải đưa vào tính toán tỷ số giữa chúng n = ,

trong đó: cx - khoảng cách giữa các gối trong phạm vi đáy ụ; cy - khoảng cách giữa các gối trong phạm vi tường ụ;

ri - hệ số qui đổi, không thứ nguyên, đặc trưng cho độ cứng của nhịp thứ i. ri = Dc/Di khi 1 i n,

ri = Dc/ ( Di.n) khi (n+2) i (p+1), (p+3) i (q+1); Di -độ cứng trụ trong phạm vi nhịp thứ i .

EJ

Di 

i .

1 2

(VI-18)

(EJ)i - độ cứng của phần tử i ; - hệ số Poát xông của vật liệu kết cấu. Nếu trong nhịp độ cứng thay đổi thì nó được xác định theo hình VI-40.

Để xác định ri trong hệ số khi ẩn số nằm trên đường chéo chính, độ cứng qui đổi

được xác định như sau:

- để xác định hệ số của mômen Mi ở gối i thì theo công thức:

EInh 

3



.1 + + 2 ,

(VI-19)

- để tính hệ số của mômen Mi-1 trên gối i-1 thì dùng công thức:

EInh'  E .

(VI-20)



i 1+ + 2 3

' ''

i i

http://www.ebook.edu.vn 158

Bảng VI-9. Hàm ΔFj (k -1)k và ΔFj (k +1)k .

Hàm

c/H				j	-	k	
c/H	0	1	2	3	4	5
ΔFj (k-1)k khi j <k	0 1/32 1/16	- - -	3.2958 3.2948 3.2918	1.4556 1.4525 1.4433	0.8228 0.8177 0.8028	0.5795 0.5724 0.5517	0.4481 0.4391 0.4130
ΔFj(k+1)k khi j >k	1/2 1 2	- - -	3.0582 2.5409 1.5983	0.8846 0.2256 -	0.1475 - -	- - -	- - -
	4	-	0.7950	-	-	-	-
ΔFj (k-1)k khi j <k	0 1/32 1/16	-3.2958 -3.2948 -3.2918	-1.4556 -1.4525 -1.4433	-0.8228 -0.8177 -0.8028	-0.5795 -0.5724 -0.5517	-0.4481 -0.4391 -0.4130	-0.3657 -0.3547 -0.3234
ΔFj(k+1)k khi j >k	1/2 1 2	-3.0582 -2.5409 -1.5983	-0.8846 -0.2256 -	-0.1475 - -	- - -	- - -	- - -
	4	-0.7950	-	-	-	-	-
Hàm	c/H	j - k 
Hàm	c/H	6	7	8	9	10	11
ΔFj (k-1)k khi j <k	0 1/32 1/16	0.3657 0.3547 0.3234	0.3089 0.2960 0.2602	0.2675 0.2526 0.2129	0.2358 0.2191 0.1758	0.2109 0.1925 0.1460	0.1908 0.1705 0.1217
ΔFj(k+1)k khi j >k	1/2 1 2	- - -	- - -	- - -	- - -	- - -	- - -
	4	-	-	-	-	-	-

http://www.ebook.edu.vn 159

Hàm

c/H



ΔFj (k-1)k khi j <k

1/32

1/16

-0.3089

-0.2960

-0.2602

-0.2675

-0.2526

-0.2109

-0.2358

-0.2191

-0.1758

-0.2109

-0.1925

-0.1460

-0.1908

-0.1705

-0.1217

-0.1741

-0.1522

-0.1013

ΔFj(k+1)k khi j >k

1/2

ΔFj (k-1)k khi j <k

1/32

1/16

0.1741

0.1522

0.1013

0.1602

0.1483

0.1380

0.1291

0.1213

ΔFj(k+1)k khi j >k

1/2

ΔFj (k-1)k khi j <k

1/32

1/16

-0.1602

-0.1483

-0.1380

-0.1291

-0.1213

ΔFj(k+1)k khi j >k

1/2

http://www.ebook.edu.vn 160

Độ cứng qui đổi ứng với ri trong hệ số của các ẩn số không nằm trên đường chéo chính sẽ được xác định theo công thức

EInh''  E .

(VI-21)

i 2 2 1

2 2 1



Trong các phương trình còn có những đại lượng sau:

- Đại lượng , được gọi là hàm Giêmôskin,

 c3

o x

(VI-22)

c o

6D 1 2 

Trong đó Eo và o tương ứng là môđun biến dạng và hệ số Poat xông của đất nền;

- Đặc trưng giả định của nền Ao

Ao 

o

1 2

; (VI-23)

-Hệ số độ cứng tương đối của gối ở góc k theo hướng nằm ngang

k 

Kn  Km

, (VI-24)

Trong đó Kk và Km - các hệ số độ mềm ở gối k và gối m trên hướng ngang. Thường Kk = Km và k =0,5;

- Dịch chuyển ban đầu của gối i theo phương trục x

Xo  Ro . K

, (VI-25)

i i i

Trong đó Ri - phản lực tại gối i do ngoại lực gây ra khi xem các nhịp lân cận là không liên tục và lấy dấu dương khi nó hướng vào công trình;

- Các góc xoay của tiết diện o , o liền kề gối i từ phía trái và phía phải do ngoại

i i+1

lực gây ra trong hệ cơ bản, và lấy dấu dương khi nó làm đường đàn hồi lồi về phía đất nền. Khi xác định các số hạng tự do của hệ phương trình chính tắc với công trình trên lớp chịu nén do lực ngoài thì có thể bỏ qua các góc xoay trên.

- Các góc xoay của các tiết diện gối do nhiệt độ được xác định theo công thức



o , o

t .ci . i ,

(VI-26)

Trong đó: t - hệ số giãn nở vì nhiệt của vật liệu công trình; ci - chiều dài nhịp i ; i -phân bố độ chênh nhiệt độ theo chiều cao tiết diện trong nhịp i .

Δ0

i

i h

, (VI-27)

Trong đó Ti - độ chênh nhiệt độ trong nhịp thứ i ; hi - chiều cao tiết diện trong nhịp thứ i .

Biểu diễn dưới dạng ma trận, hệ phương trình chính tắc của phương pháp lực: A.M + P = 0, (VI-28)

Trong đó A-ma trận vuông đối xứng cấp (q-2 ) của các hệ số của các ẩn lực là mômen Mi; q - số nút gối chung của hệ; M-ma trận cột của các ẩn lực Mi; P - ma trận các số hạng tự do.

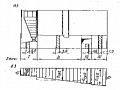
Cấu trúc của ma trận A cho trên hình VI-41.

http://www.ebook.edu.vn 161

Hình VI-41. Cấu trúc ma trận A để tính buồng ụ có cônxôn đáy trên lớp đàn hồi chịu nén. Phần gạch chéo ứng với buồng không có cônxôn đáy; phần viền đậm ứng với sơ đồ dầm; '''' - phần tử phụ thuộc độ cứng của dầm và nền; '''' - phần tử không phụ thuộc độ cứng.

Giới hạn áp dụng các công thức xác định các phần tử của ma trận M thay đổi tuỳ theo phương pháp tính toán và sơ đồ tính. Chẳng hạn đối với buồng ụ không có cônxôn đáy thì hệ số qui đổi ri được xác định theo công thức sau:

⎧Dc

⎪⎪Di

ri ⎨1

khi k + 1 i  m,

(VI-29)

⎪.ckhi 1 i k, m + 1 i  n.

⎪⎩ n Di

Các công thức xác định các phần tử của ma trận đối xứng A khi công trình đối xứng

đặt trên lớp đần hồi chịu nén có cônxôn đáy sẽ có dạng:

http://www.ebook.edu.vn 162

⎧2r  r 



, 1 i k - 1 , k + 1 i ⎛n⎞; ⎫

⎪i i1 0

⎪

n 2i

⎜⎝1⎟⎠⎪

⎪

⎪k p 1 0 0

p k k

m1 k

0 k k⎪

⎪⎪2r 

 r 

 A n2 K

 K 



 A n2K 

, i = k'' ;⎪⎪

i j ⎨

p 1 k 1 0 0

p k k m k

0 k k

⎬j = i

⎪r  r  0,5,0, i = n; ⎪

⎪i i1 0 ⎪

⎪2 ⎪

i i1 0

i1

i i1

⎪2r  r  A n2 K  4K  K , n+ 2 i p  1; ⎪

⎪⎩

p p1 0

p1

p k k

k k

⎪⎭

⎪2r  r  A n2K  4K  K A n2K , i = p ; ⎪

⎧ r



, 1 i k - 2,k + 1 i ⎛n 2⎞⎫

⎪i 1

⎪

n 2i1

⎜⎝2

⎟⎠;⎪

⎪

⎪ rk01m k 2 , i = k - 1 ; ⎪

⎪ r



⎪-2 r  A n2K , i = k' ; ⎪

i j



, i = k'';

⎪

⎨

p1 1 0 n k

⎬j = i + 1



⎪p1 0 1 mk m k1 ⎪

⎪ r , i = n -1; ⎪

⎪k 1 2 ⎪

⎪2 ⎪

⎪⎩ ri1  2A0n

Ki Ki1,

n + 2 i p 1; ⎪⎭





⎧

⎪2 n 2i 2

⎪

, 1 i k- 3, k+ 1i ⎛⎜n

⎝

⎞⎫

⎠

3⎟;⎪

⎪

⎪12m k 3 m k 2 , i = k - 2; ⎪

⎪

⎪

⎪

1



m k m k1



, i = k - 1;

, i = k';

⎪

j = i + 2

i j ⎨2

⎪



m k 2



mk1

⎬

, i = k''; ⎪

⎪

⎪1 2

m k1

m k 2 ⎪

;0, i = n 2; ⎪

⎪2 ⎪

⎪A n2K ,

n + 2 i p  2. ⎪

⎩0 i1 ⎭

http://www.ebook.edu.vn 163

⎫

⎧, 1 i k - 1, k + 1 i ⎛n  4⎞; ⎧n

⎪N n 2i N

⎪

⎪⎪

⎜⎝2

⎟⎠⎪

⎪

⎪j = i + N ,

⎪

ij

⎨

N N 1



m k N 2

mk N1

, i = k';

⎬⎨N  2;

⎪

⎪

⎪⎩

N 1

N m k N1

mk N

, i = k'';

⎪⎪j  k', j  k''.

⎪

⎭

⎪⎪⎩



⎧

⎪N  ji,

⎪

1 i k - 1,k  1 i ⎛⎜n 

⎞⎫

⎟⎠ ;⎪

⎬

⎪

⎝2

⎨



ij

⎪



N N 1

, 0,

i = k';

⎪j = n



⎪

⎪N 1



⎩⎪

, 0,

i = k''; ⎪2

⎪

⎭⎪

⎧

⎪

⎪

k1i

ki

m1i

m1i

mi,1 i k + 3, j  k ;

⎬

mi,1 i k - 2, j  k ;

⎪

⎪A n2K ,

i = k'; ⎫



ij ⎨2

⎪

j = p - 1

⎪A0n Kp,

⎪

i = k ;⎪⎭

⎪-r  A n2 2K

 K 

A n2K 

,i  k';⎫

p+1 0

⎪

p k k

0 k k

⎪

⎬j = p

⎪ r  A n2 2K

 K 

A n2K 

,i  k''. ⎪⎭

⎩p 1 0

p k k

0 k k

C¸c dÊu `+` vµ `` dïng cho tÝnh to¸n c¸c s¬ ®å t¶i träng ®èi xøng, cßn `` cho t¶i träng ph¶n xøng. Nh÷ng tr−êng hîp kh¸c ngoµi nh÷ng tr−êng hîp chØ ra trong c¸c c«ng thøc trªn Þj =0.

C¸c c«ng thøc ®Ó x¸c ®Þnh c¸c phÇn tö cđa ma trËn P khi c«ng tr×nh ®èi xøng ®Æt trªn líp ®µn håi chÞu nÐn vµ cã c«n x«n ®¸y th× ®−îc x¸c ®Þnh theo c«ng thøc sau:

http://www.ebook.edu.vn 164