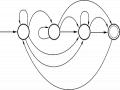
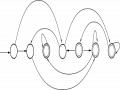
a) - Xây dựng NFA tương đương với NFA NFA M = <Q, , , q0, F>:
+ Q = {A, B, C};
+ = {0, 1};
+ q0 = A ;
+ F = {B, C};
+ :
C C
NFA M‟ = <Q, , ‟, q0, F‟>:
+ F‟ = {B, C} vì -Closure(q0) = -Closure(A) = {A} -Closure(q0) F = ;
+ ‟:
1. ‟(A, 0) = *(A, 0) = -Closure((-Closure(A), 0)) = {B}
2. ‟(A, 1) = *(A, 1) = -Closure((-Closure(A), 1)) = {A, C}
3. ‟(B, 0) = *(B, 0) = -Closure((-Closure(B), 0)) = {A}
4. ‟(B, 1) = *(B, 1) = -Closure((-Closure(B), 1)) =
5. ‟(C, 0) = *(C, 0) = -Closure((-Closure(C), 0)) = {B}
6. ‟(C, 1) = *(C, 1) = -Closure((-Closure(C), 1)) =
- Xây dựng DFA tương đương với NFA
D = < Q”, ”, ”, q”0, F” >:
+ Q” = {[A], [B], [C], [A, B], [A, C], [B, C], [A, B, C]}
= { q0 , q1 , q2 , q3 , q4 , q5 , q6 }
+ ” = {0, 1};
+ q”0 = [A] = q0;
+ F” = {q1, q2 , q3 , q4 , q5 , q6 };
+ ”:
”(q0, 0) = q1; ”(q0, 1) = q4;
”(q1, 0) = q0; ”(q1, 1) = ;
”(q2, 0) = q1; ”(q2, 1) = ;
”(q3, 0) = q3; ”(q3, 1) = q4 ;
”(q4, 0) = q1; ”(q4, 1) = q4 ;
”(q5, 0) = q3; ”(q5, 1) = ;
”(q6, 0) = q3; ”(q6, 1) = q4.
b) - Xây dựng DFA tương đương với NFA
D = < Q, , , q0, F >:
+ Q = {[A], [B], [C], [A, B], [A, C], [B, C], [A, B, C]}
= {q0 , q1 , q2 , q3 , q4 , q5 , q6 }
+ = {0, 1};
+ q0 = [A] = q0;
+ F = {q0, q3 , q4, q6};
+ :
(q0, 0) = q0; (q0, 1) = q1;
(q1, 0) = ; (q1, 1) = q5;
(q2, 0) = q3; (q2, 1) = ;
(q3, 0) = q0; (q3, 1) = q5;
(q4, 0) = q3; (q4, 1) = q1;
(q5, 0) = q3; (q5, 1) = q5;
(q6, 0) = q3; (q6, 1) = q5.
2.31. 1) 0(1 + 2) 3+
2) 3* (0 + 1 + 2)*
3) (0 + 1)* (2 + 3)*
2.32. 1) Mô tả (bằng lời) ngôn ngữ được biểu diễn bằng mỗi biểu thức
a) Tập hợp các xâu: Mở đầu bằng một ký tự 0, tiếp theo là một dãy các ký tự 0 hoặc 1, cuối cùng là dãy một hoặc nhiều ký tự 0.
b) Tập hợp các xâu: Gồm một hoặc nhiều dãy các ký tự được mở đầu bằng dãy các ký tự 0 hoặc 1, tiếp theo là ký tự 0, kết thúc bằng ký tự 0 hoặc 1.
c) Tập hợp các xâu: Mở đầu bằng một ký tự 0 hoặc 1, tiếp theo là 2 ký tự 0, kết thúc là dãy các ký tự 0 hoặc là dãy một hoặc nhiều ký tự 1.
d) Tập hợp các xâu: Mở đầu bằng một dãy không, một hoặc nhiều lần dãy các ký tự a hoặc ba hoặc aab, kết thúc bằng dãy không, một hoặc nhiều ký tự a.
2) Xây dựng NFAε tương đương với mỗi biểu thức a) r = 0(0 + 1)* 0+
+ Phân tích r
- Ta có r = r r ; r = 0(0 + 1)*; r = 0+.
1 2 1 2
- r = r r ; r = 0; r = (0 + 1)*.
1 3 4 3 4
- r = (r )* ; r = (0 + 1).
3 5 5
- r = r + r ; r = 0; r = 1.
5 6 7 6 7
- r = (r ) + ; r = 0.
2 8 8
+ Xây dựng r
Start
0
0
1
- r = 0
3
Start
2
0
3
- r = 0
6
Start
4
1
5
- r = 1
7
- r = 0
Start
6
0
7
8
0
Start
ε
2
3
ε
8 9
ε
4
1
5
ε
- r = r + r
5 6 7
- r = (r )*
4 5
0
Start
10
ε
2
3
ε
8
9
11
ε
4
1
5
ε
ε
ε
- r = r r
1 3 4
ε
0
Start
0
0
1
ε
2
3
ε
8
9
11
ε
4
1
5
ε
ε
- r = (r ) +
2 8 ε
Start
12
6
0
7
13
- r = r r
ε
1 2
0
ε
2
3
ε
Start
0
0
1
8
9
11
ε
4
1
5
ε
ε
ε
*
b) r = ((0+ 1)
0(0 + 1))+
ε
+ Phân tích r
6
0
7
13
+ *
- Ta có r = (r ) ; r = (0+ 1) 0(0 + 1)
1 1
*
- r = r
1 2
r ; r
3 2
= (0+ 1) 0; r
3
*
= (0 + 1)
- r = r
2 4
r ; r = (0+ 1)
5 4
*
; r = 0
5
- r = (r
4 6
) ; r
6
= 0 + 1
- r = r + r ; r = 0; r = 1
6 7 8 7 8
- r = r + r ; r = 0; r = 1
3 9 10 9 10
+ Xây dựng r
- Xây dựng r = 0; r = 0; r = 1; r = 0; r = 1
5 7 8 9 10
- Xây dựng r = r + r
6 7 8
*
- Xây dựng r
4
= (r )
6
- Xây dựng r2 = r4 r5
- Xây dựng r3 = r9 + r10
- Xây dựng r1 = r2 r3
- Xây dựng r = (r1)+ c) r = (1+ 0)00 (0* + 1+)
+ Phân tích r
- Ta có r = r1 r2; r1= (1+ 0)00; r2= (0* + 1+)
- r1 = r3 r4; r3 = (1+ 0)0; r4 = 0
- r3 = r5 r6 ; r5= 1+ 0; r6 = 0
- r5 = r7 + r8 ; r7 = 1; r8 = 0
- r2 = r9+ r10 ; r9 = 0*; r10 = 1+
- r9 = (r11) * ; r11 = 0
- r10 = (r12) +; r12 = 1
+ Xây dựng r
- Xây dựng r4 = 0; r6 = 0; r7 = 1; r8 = 0; r11 = 0; r12 = 1
- Xây dựng r5 = r7+ r8
- Xây dựng r3 = r5 r6
- Xây dựng r1 = r3 r4
- Xây dựng r9 = (r11) *
- Xây dựng r = (r ) +
10 12
- Xây dựng r = r + r
2 9 10
- Xây dựng r = r + r
2 9 10
- Xây dựng r = r r
1 2
*
d) r = (a + ba + aab) (ε + a)+
+ Phân tích r
* +
- Ta có r = r r ; r = (a + ba + aab) ; r = (ε + a)
0 2 0 2
- r0 = (r1) * ; r1= (a + ba + aab)
- r1 = r3 + r4; r3 = a + ba ; r4 = aab
- r3 = r5 + r6 ; r5= a; r6 = ba
- r6= r7 r8 ; r7 = b; r8 = a
- r4 = r9 r10 ; r9 = aa; r10 = b
- r9 = r11 r12 ; r11 = a; r12 = a
- r2 = (r13) +; r13 = ε + a
- r13 = r14 + r15; r14 = ε; r15 = a
+ Xây dựng r
- Xây dựng r5= a; r7 = b; r8 = a; r10 = b; r11 = a; r12 = a; r14 = ε; r15 = a
- Xây dựng r9= r11 r12
- Xây dựng r4 = r9 r10
- Xây dựng r6= r7 r8
- Xây dựng r3 = r5 + r6
- Xây dựng r1 = r3 + r4
- Xây dựng r0 = (r1) *
- Xây dựng r13 = r14 + r15
- Xây dựng r2 = (r13) +
2.33. 1) M1
a) M1 = <Q, , , q0, F>:
- Q = {0, 1, 2, 3};
- = {a, b};
- q0 = 0 ;
- F = {3};
- :
a b1
1 a b2
b3
a3
b) Biểu diễn M1 dưới dạng bảng.
- q0 = 0 ;
- F = {3};
- :
a | b | | |
0 | {1} | {1} | {1} |
1 | {3} | {2} | |
2 | {1} | ||
3 | {3} |
Có thể bạn quan tâm!
-
Ngôn ngữ hình thức - 23 -
Ngôn ngữ hình thức - 24 -
Ngôn ngữ hình thức - 25 -
Ngôn ngữ hình thức - 27 -
Ngôn ngữ hình thức - 28 -
Ngôn ngữ hình thức - 29
Xem toàn bộ 254 trang tài liệu này.
c) Xây dựng văn phạm tuyến tính phải tương đương với M1. G = (N, T, P, S):
- N = {0, 1, 2, 3};
- T = {a, b};
- P :
0 a1 b1 1; 1 a3 a b2; 2 b1; 3 a3 a;
- S = 0.
M1.
d) Xây dựng văn phạm tuyến tính trái tương đương với M1.
- Xây dựng M‟1 đảo ngược của M1; M‟1 = <Q, , ‟, q‟0, F‟>:
+ Q = {0, 1, 2, 3};
+ = {a, b};
+ q‟0 = 3 ;
+ F‟ = {0};
+ ‟:
’ a’ b0’
’ 3 a’ b1
’ b2
’ a3
- Xây dựng văn phạm tuyến tính phải G‟ = (N‟, T‟, P‟, S‟) tương ứng với M‟1; N= {3, 2, 1, 0}; T = {a, b}; S = 3;
P: 3 a1 b2 a3; 2 b1;
1 a0 a b0 b0.
- Xây dựng văn phạm tuyến tính trái G đảo ngược của G‟ và tương đưng với
N‟ = {3, 2, 1, 0}; T‟ = {a, b}; S‟ = 3 ;
P‟: 3 1a 2b 3a; 2 1b;
1 0a a 0b b0.
e) Biểu thức chính quy tương đương với M1.
Từ đồ thị suy ra biểu thức chính quy r1 = (a b )(bb a)a*
2) M2
a) M2 = <Q, , , q0, F>:
- Q = {0, 1, 2, 3, 4};
- = {a, b};