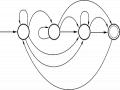
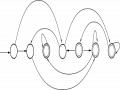
2.17. 1) Biểu diễn M
a) Dạng bảng:
- q0 = 0 ;
- F = 3;
- :
a | b | c | |
0 | 1 | 1 | 1 |
1 | 1 | 2 | |
2 | 3 | 4 | |
3 | 4 | ||
4 | 2 | 4 | 3 |
Có thể bạn quan tâm!
-
Ngôn ngữ hình thức - 20 -
Ngôn ngữ hình thức - 21 -
Ngôn ngữ hình thức - 22 -
Ngôn ngữ hình thức - 24 -
Ngôn ngữ hình thức - 25 -
Ngôn ngữ hình thức - 26
Xem toàn bộ 254 trang tài liệu này.
b) Dạng đồ thị:
a a
Start 0 b 1 b c
a
b
2 b 4 c 3
a a
2) Automat M là Automat hữu hạn đơn định; vì qQ và a, ta có:
(q, a) 1
3) - (1, aaabbaaaabc)
+ (1, a) = 1; (1, a) = 1; (1, a) = 1;
+ (1, b) = 2;
+ (2, b) = 4;
+ (4, a) = 2;
+ (2, a) = 3;
+ (3, a) = 4;
+ (4, a) = 2;
+ (2, b) = 4;
+ (4, c) = 3.
(1, aaabbaaaabc) = 3.
- (0, cabaabba);
+ (0, c) = 1;
+ (1, a) = 1;
+ (1, b) = 2;
+ (2, a) = 3;
+ (3, a) = 4;
+ (4, b) = 4; (4, b) = 4;
+ (4, a) = 2;
(0, cabaabba)= 2.
4) - w = caabaaabca
q | c | |
khởi tạo | 0 | c |
1 | 1 | a |
2 | 1 | a |
3 | 1 | b |
4 | 2 | a |
5 | 3 | a |
6 | 4 | a |
7 | 2 | b |
8 | 4 | c |
9 | 3 | a |
10 | 4 | $ |
Ta có q = 4 F. Vậy automat trên không đoán nhận được từ w = caabaaabca.
- w = aaaabbbc.
q | c | |
khởi tạo | 0 | a |
1 | 1 | a |
2 | 1 | a |
3 | 1 | a |
4 | 1 | b |
5 | 2 | b |
6 | 4 | b |
7 | 4 | c |
8 | 3 | $ |
Ta có q = 3 F. Vậy automat trên đoán nhận được từ w = aaaabbbc.
2.18. 1) Biểu diễn M
a) Dạng bảng:
- q0 = A ;
- F = E;
- :
a | b | |
A | {A, B} | {B} |
B | {D, E} | {C, E} |
C | {D, E} | {D} |
D | {C} | {E} |
E | {E} |
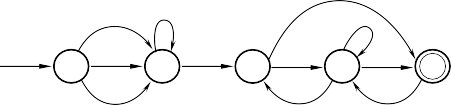
b) Dạng đồ thị:
a
a
b
a
a
a
Start
A
b
B
b
C
a
b a
D
b
E
a
2) Automat M là Automat hữu hạn không đơn định; vì AQ và a, ta có:
(A, a) = {A, B} = 2 1
3) - (A, aaabbaaaa)
+ (A, a) = {A, B};
+ ({A, B}, a) = (A, a) (B, a) = {A, B}{D, E}= {A, B, D, E};
+ ({A, B, D, E}, a) = {A, B, C, D, E};
+ ({A, B, C, D, E}, b) = {B, C, D, E};
+ ({B, C, D, E}, b) = {C, D, E };
({C, D, E}, a) = {C, D, E};
+ ({C, D, E}, a) = {C, D, E};
+ ({C, D, E}, a) = {C, D, E};
+ ({C, D, E}, a) = {C, D, E}.
(A, aaabbaaaa) = {C, D, E}.
- (C, abaabbaa);
+ (C, a) = {D, E};
+ ({D, E}, b) = {E};
+ ({E}, a) = (E, a) = {E};
+ ({E}, a) = {E};
+ ({E}, b) = ;
+ (, b) = ;
+ (, a) = .
(C, abaabbaa)= .
4) - w = aabaaaaa$
Ta trình bày giải thuật sử dụng automat không đơn định đoán nhận w bằng bảng sau:
q = (q, c) | c | |
khởi tạo | A | a |
1 | {A, B} | a |
2 | {A, B, D, E} | b |
3 | {B, C, E} | a |
4 | {D, E} | a |
5 | {C, E} | a |
6 | {D, E} | a |
7 | {C, E} | a |
8 | {D, E} | $ |
Ta có q F = {D, E} {E} = {E} . Vậy automat trên đoán nhận được từ w = aabaaaaa.
- w = aaaababbb$
q = (q, c) | c | |
khởi tạo | A | a |
1 | {A, B} | a |
2 | {A, B, D, E} | a |
3 | {A, B,C, D, E} | a |
4 | {A, B, C, D, E} | b |
5 | {B, C, D, E} | a |
6 | {C, D, E} | b |
7 | {D, E} | b |
8 | {E} | b |
9 | {E} | $ |
Ta có q F = {E} {E} = {E} . Vậy w = aaaababbb L(M).
2.19. 1) Biểu diễn M
a) Dạng bảng:
- q0 = 0 ;
- F = 3;
- :
a | b | c | |
0 | {0,1} | {2} | {2} |
1 | {1, 2} | {1, 2, 3} | |
2 | {3} | {2, 3} | {3} |
3 | {3} | {2} | {3} |
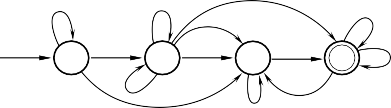
b) Dạng đồ thị:
a a b c b
Start 0 a b
1 a
b,c
2 a,b,c 3 a b
b
2) Automat M là Automat hữu hạn không đơn định; vì 1Q và b, ta có:
(1, b) = {1, 2, 3} = 3 1
3) - (1, aaabbaaaabc)
+ (1, a) = {0,1}
+ ({0,1}, a) = {0, 1, 2};
+ ({0,1,2}, a) = {0, 1, 2, 3};
+ ({0,1,2,3}, b) = {1, 2, 3};
+ ({1, 2, 3}, b) = {1, 2, 3};
+ ({1, 2, 3}, a) = {1, 2, 3};
+ ({1, 2, 3}, a) = {1, 2, 3};
+ ({1, 2, 3}, a) = {1, 2, 3};
+ ({1, 2, 3}, a) = {1, 2, 3};
+ ({1, 2, 3}, b) = {1, 2, 3};
+ ({1, 2, 3}, c) = {2, 3};
(1, aaabbaaaabc) = {2, 3}.
- (0, cabaabba);
+ (0, c) = 2;
+ (2, a) = 3;
+ (3, b) = 2;
+ (2, a) = 3;
+ (3, a) = 3;
+ (3, b) = 2;
+ (2, b) = {2, 3};
+ ({2, 3}, a) = 3;
(0, cabaabba)= 3.
4) - w = caabaaabca
q = (q, c) | c | |
khởi tạo | 0 | c |
1 | 2 | a |
2 | 3 | a |
3 | 3 | b |
4 | 2 | a |
5 | 3 | a |
6 | 3 | a |
7 | 3 | b |
8 | 2 | c |
9 | 3 | a |
10 | 3 | $ |
Ta có q F = {3} . Vậy automat trên không đoán nhận được từ w = caabaaabca.
- w = aaaabbbc.
q = (q, c) | c | |
khởi tạo | 0 | a |
1 | {0, 1} | a |
2 | {0, 1, 2} | a |
3 | {0, 1, 2, 3} | a |
4 | {0, 1, 2, 3} | b |
5 | {1, 2, 3} | b |
6 | {1, 2, 3} | b |
7 | {1, 2, 3} | c |
8 | {2, 3} | $ |
Ta có q F = {3} . Vậy automat trên đoán nhận được từ w = aaaabbbc.
2.20. 1) - Biểu diễn M dưới dạng bảng:
+ q0 = A ;
+ F = E;
+ :
a | b | | |
A | {A, B} | {B} | {B} |
B | {D, E} | {C, E} | |
C | {D, E} | {D} | |
D | {D, E} | ||
E | {E} | {A} |
- Biểu diễn M dưới dạng đồ thị:
a
b
a
a
a
Start
A
b
B
b
C
a
D
b
E
b
b
a
a
2) Automat M thuộc dạng NFA vì A Q mà (A, ) = {B}. 3) - + -CLOSURE(A) = {A, B};
+ -CLOSURE(E) = {E, A, B};
- + (A, a) = {A, B};
+ *(A, a) = -CLOSURE((-CLOSURE(A), a)) = -CLOSURE(({A, B}, a))
= -CLOSURE((A, a) (B, a)) = -CLOSURE({A, B} {D, E})
= -CLOSURE({A, B, D, E})
= -CLOSURE(A) -CLOSURE(B) -CLOSURE( D) -CLOSURE(E)
= {A, B}{B}{D}{E, A, B} = {A, B, D, E};
- + (E, a) = {E};
+ *(E, a) = -CLOSURE((-CLOSURE(E), a))
= -CLOSURE(({A, B, E}, a))