Trang chủ / Tài liệu miễn phí / Tập Bài Giảng

Ngôn ngữ hình thức - 25


(1, a) = {1, 2};

(3, ) = {4};

(4, b) = {4};

2) Biểu diễn M dưới dạng bảng

M = <Q, , , q0, F> trong đó:

- q0 = 0 ;

- F = 2, 4;

- :


Q

a

b

0

{3}

{0}

{1}

1

{1, 2}



2




3



{4}

4


{4}


Có thể bạn quan tâm!

Xem toàn bộ 254 trang tài liệu này.


3) Automat M thuộc dạng NFA vì 3 Q, ta có (3, ) = {4}.

4) Sử dụng giải thuật kiểm tra các từ sau có thuộc ngôn ngữ L(M) không?:

- w = bbbbabb


Bước

q = -closure((q,c))

c

khởi tạo

{0, 1}

b

1

{0, 1}

b

2

{0, 1}

b

3

{0, 1}

b

4

{0, 1}

a

5

{1, 2, 3, 4}

b

6

{4}

b

7

{4}

$

q F = {4} w = bbbbabb L(M).


- w = abababa


Bước

q = -closure((q,c))

c

khởi tạo

{0, 1}

a

1

{1, 2, 3, 4}

b

2

{4}

a

3

b

4

a

5

b

6

a

7

$

q F = w = abababa L(M).

2.26. 1) Chuyển M về dạng DFA D tương đương

D = <Q, , , q0, F>:

- Q = {[q1], [q2], [q3], [q1, q2], [q1, q3], [q2, q3], [q1, q2, q3]}

= {A, B, C, D, E, G, H};

- = {0, 1};

- q0 = [q1] = A;

- F = {[q3], [q1, q3], [q2, q3], [q1, q2, q3]} = {C, E, G, H};

- :

+ (A, 0) = ([q1], 0) = (q1, 0) = {q1, q2} = [q1, q2] = D (A, 0) = D;

+ (A, 1) = ([q1], 1) = (q1, 1) = {q2} = [q2] = B (A, 1) = B;

+ (B, 0) = ([q2], 0) = (q2, 0) = {q2, q3} = [q2, q3] = G (B, 0) = G;

+ (B, 1) = ([q2], 1) = (q2, 1) = ;

+ (C, 0) = ([q3], 0) = (q3, 0) = ;

+ (C, 1) = ([q3], 1) = (q3, 1) = {q3} = [q3] = C (C, 1) = C;

+ (D, 0) = ([q1, q2], 0) = (q1, 0) (q2, 0) = {q1, q2} {q2, q3} = {q1, q2, q3}

= [q1, q2, q3] = H (D, 0) = H;

+ (D, 1) = ([q1, q2], 1) = (q1, 1) (q2, 1) = [q2] = B (D, 1) = B;

+ (E, 0) = ([q1, q3], 0) = (q1, 0) (q3, 0) = {q1, q2} = [q1, q2] = D (E, 0) = D;

+ (E, 1) = ([q1, q3], 1) = (q1, 1) (q3, 1) = {q2, q3} = [q2, q3] = G (E, 1) = G;

+ (G, 0) = ([q2, q3], 0) = (q2, 0) (q3, 0) = {q2, q3} = [q2, q3] = G (G, 0) = G;

+ (G, 1) = ([q2, q3], 1) = (q2, 1) (q3, 1) = {q3} = [q3] = C (G, 1) = C;


+ (H, 0) = ([q1, q2, q3], 0) = (q1, 0) (q2, 0) (q3, 0) = {q1, q2, q3} =

[q1, q2, q3] = H (H, 0) = H;

+ (H, 1) = ([q1, q2, q3], 1) = (q1, 1) (q2, 1) (q3, 1) = {q2, q3} = [q2, q3]

= E (H, 1) = E.

2) Biểu diễn D dưới dạng đồ thị


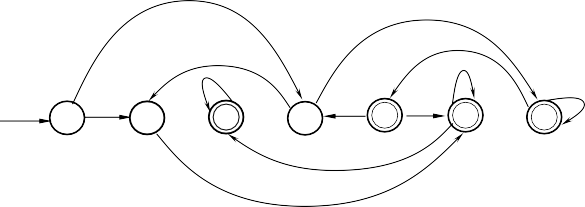
0 1 1 Start A 1 B C D 0 E 0 1 0 0 1 G H 0 1 0 2 27 1 Chuyển M về dạng DFA D tương 1

0


1

1

Start A 1 B C


D 0 E


0

1

0 0

1 G H 0


1


0

2.27. 1) Chuyển M về dạng DFA D tương đương

D = <Q, , , q0, F>:

- Q = {[q1], [q2], [q3], [q4], [q1, q2], [q1, q3], [q1, q4] [q2, q3], [q2, q4], [q3, q4], [q1, q2, q3], A B C D E F G H I J K

[q1, q2, q4], [q2, q3, q4], [q1, q3, q4], [q1, q2, q3, q4]} M N O P

= {A, B, C, D, E, F, G, H, I, J, K, M, N, O, P};

- = {0, 1};

- q0 = [q1] = A;

- F = {[q4], [q1, q4], [q2, q4], [q3, q4] , [q1, q2, q4], [q2, q3, q4], [q1, q3, q4], [q1, q2, q3, q4]}

= { D, G, I, J, M, N, O, P};

- :

+ (A, 0) = B; (A, 1) = B;

+ (B, 0) = H;

+ (B, 1) = ;

+ (C, 0) = D; (C, 1) = D;


+ (D, 0) = ; (D, 1) = ;

+ (E, 0) = H; (E, 1) = B;

+ (F, 0) = I; (F, 1) = I;

+ (G, 0) = B; (G, 1) = B;

+ (H, 0) = N; (H, 1) = D;

+ (I, 0) = H; (I, 1) = ;

+ (J, 0) = D; (J, 1) = D;

+ (K, 0) = N; (K, 1) = I;

+ (M, 0) = H; (M, 1) = B;

+ (N, 0) = N; (N, 1) = D;

+ (O, 0) = I; (O, 1) = I;

+ (P, 0) = N; (P, 1) = I.

2) Biểu diễn D dưới dạng bảng

- q0 = A;

- F = {D, G, I, J, M, N, O, P};

- :


Q

0

1

A

B

B

B

H


C

D

D

D



E

H

B

F

I

I

G

B

B

H

N

D

I


H

J

D

D

K

N

I

M

H

B

N

N

D

O

I

I

P

N

I


2.28. 1) - Chuyển NFA M về dạng NFA M‟ tương đương

* NFA M = <Q, , , q0, F>:

+ Q = {q1, q2, q3, q4};

+ = {0, 1};

+ q0 = q1 ;

+ F = {q4};

+ :

 q1q2 q1q2

 q2q2 q3

 q3q4

 q3q2 q4

* NFA M‟ = <Q, , ‟, q1, F‟>:

+ F‟ = {q4} vì -Closure(q1) = {q1, q2} -Closure(q1) F = ;

+ ‟:

1. ‟(q1, 0) = *( q1, 0) = -Closure((-Closure(q1), 0)) = {q2, q3, q4}

2. ‟(q1, 1) = *(q1, 1) = -Closure((-Closure(q1), 1)) =

3. ‟(q2, 0) = *(q2, 0) = -Closure((-Closure(q2), 0)) = {q2, q3, q4}

4. ‟(q2, 1) = *(q2, 1) = -Closure((-Closure(q2), 1)) =

5. ‟(q3, 0) = *(q3, 0) = -Closure((-Closure(q3), 0)) = {q2, q3, q4}

6. ‟(q3, 1) = *(q3, 1) = -Closure((-Closure(q3), 1)) = {q4}

7. ‟(q4, 0) = *(q4, 0) = -Closure((-Closure(q4), 0)) =

8. ‟(q4, 1) = *(q4, 1) = -Closure((-Closure(q4), 1)) =

- Biểu diễn M‟ dưới dạng bảng

’:


Q

0

1

q1

{q2, q3, q4}


q2

{q2, q3, q4}


q3

{q2, q3, q4}

{q4}

q4




2) Chuyển NFA M‟ về dạng DFA D tương đương D = <Q, , , q0, F>:

- Q = {[q1], [q2], [q3], [q4], [q1, q2], [q1, q3], [q1, q4] [q2, q3], [q2, q4], [q3, q4], [q1, q2, q3],

A B C D E F G H I J K [q1, q2, q4], [q2, q3, q4], [q1, q3, q4], [q1, q2, q3, q4]}

M N O P

= {A, B, C, D, E, F, G, H, I, J, K, M, N, O, P};

- = {0, 1};

- q0 = [q1] = A;

- F = {[q4], [q1, q4], [q2, q4], [q3, q4] , [q1, q2, q4], [q2, q3, q4], [q1, q3, q4], [q1, q2, q3, q4]}

= { D, G, I, J, M, N, O, P};

- :

+ (A, 0) = N; (A, 1) = ;

+ (B, 0) = N; (B, 1) = ;

+ (C, 0) = N; (C, 1) = ;

+ (D, 0) = ; (D, 1) = ;

+ (E, 0) = N; (E, 1) = ;

+ (F, 0) = N; (F, 1) = D;

+ (G, 0) = N; (G, 1) = ;

+ (H, 0) = N; (H, 1) = D;

+ (I, 0) = N; (I, 1) = ;

+ (J, 0) = N; (J, 1) = D;

+ (K, 0) = N; (K, 1) = D;

+ (M, 0) = N; (M, 1) = ;

+ (N, 0) = N; (N, 1) = D;

+ (O, 0) = N; (O, 1) = D;

+ (P, 0) = N; (P, 1) = D.

- Biểu diễn D dưới dạng đồ thị (tự làm).

2.29. 1) - Chuyển NFA M về dạng NFA M‟ tương đương và biểu diễn M‟ dưới dạng bảng

NFA M = <Q, , , q0, F>:


+ q0 = q1 ;

+ F = {q4};

+ :


Q

0

1

q1

{q1, q2}

{q2}

{q2}

q2

{q2, q3}



q3


{q4}

{q4}

q4



{q2}


NFA M‟ = <Q, , ‟, q1, F‟>:

+ F‟ = {q4} vì -Closure(q1) = {q1, q2} -Closure(q1) F = ;

+ ‟: Xác định theo công thức

‟(q, a) = *(q, a) = -Closure((-Closure(q), a)) với q Q và a .

Kết quả được cho bởi bảng sau:


Q

0

1

q1

{q1, q2, q3, q4}

{q2}

q2

{q2, q3, q4}


q3

{q2, q3, q4}

{q2, q4}

q4

{q2, q3, q4}

{q2, q4}


2) Chuyển NFA M‟ về dạng DFA D tương đương D = <Q‟, ‟, ‟‟, q‟0, F‟>:

- Q” = {[q1], [q2], [q3], [q4], [q1, q2], [q1, q3], [q1, q4] [q2, q3], [q2, q4], [q3, q4], [q1, q2, q3],

A B C D E F G H I J K [q1, q2, q4], [q2, q3, q4], [q1, q3, q4], [q1, q2, q3, q4]}

M N O P

= {A, B, C, D, E, F, G, H, I, J, K, M, N, O, P};

- ” = {0, 1};

- q”0 = [q1] = A;


- F” = {[q4], [q1, q4], [q2, q4], [q3, q4] , [q1, q2, q4], [q2, q3, q4], [q1, q3, q4], [q1, q2, q3, q4]}

= { D, G, I, J, M, N, O, P};

- ”: Xác định theo công thức

”(q, a) = ‟(q, a) với q Q” và a ”.

Kết quả được cho bởi bảng sau:


Q

0

1

A

P

B

B

N


C

N

I

D

N

I

E

P

B

F

P

I

G

P

I

H

N

I

I

N

I

J

N

I

K

P

I

M

P

I

N

N

I

O

P

I

P

P

I


- Biểu diễn D dưới dạng đồ thị (tự làm).

2.30. 1) Biểu thức chính quy tương ứng với mỗi sơ đồ. a) r = 0(00)* + 1+

b) r = 0*11*1(01*1)*00* = 0*1+(01+)*0+

2) a) Automat trên hình a) là NFA vì C Q mà (C, ) = {A}.

b) Automat trên hình b) là NFA vì B Q và 1 mà (B, 1) = {B, C}

(B, 1)= 2 > 1.

3) Xây dựng DFA tương ứng với mỗi sơ đồ.

Ngày đăng: 16/07/2022