Ngôn ngữ hình thức

- q0 = 0 ;

- F = {2, 4};

- :

 a b3

 1 a b2

 a2

 b3, 4

b) Biểu diễn M2 dưới dạng bảng.

- q0 = 0 ;

- F = {3};

- :

Q 

a	b	
0	{0}	{3}	{1, 3}
1	{2}	{2}
2	{2}
3		{3, 4}
4

Có thể bạn quan tâm!

Xem toàn bộ 254 trang tài liệu này.

c) Xây dựng văn phạm tuyến tính phải tương đương với M2. G = (N, T, P, S):

- N = {0, 1, 2, 3};

- T = {a, b};

- P :

0  a0  b3  1 3; 1  a2  a  b2 b; 2  a2 a; 3  b3 b4 b;

- S = 0.

d) Xây dựng văn phạm tuyến tính trái tương đương với M2

+ Chuyển M về FA M21 tương đương có một trạng thái kết thúc

- Q = {0, 1, 2, 3, 4, 5};

-  = {a, b};

- q0 = 0 ;

- F = {5};

- :

 a b3

 1 a b2

 a25

 b3, 4

5

+ Xây dựng M‟2 đảo ngược của M21; M‟2 = <Q‟, ‟, ‟, q‟0, F‟>:

+ Q‟ = {0, 1, 2, 3, 4, 5};

+ ‟ = {a, b};

+ q‟0 = 5 ;

+ F‟ = {0};

+ ‟:

 a b

 2 a1 b1

 a2

 b3 b3

4

- Xây dựng văn phạm tuyến tính phải G‟ = (N‟, T‟, P‟, S‟) tương ứng với M‟2; G‟ = (N, T, P‟, S):

- N = {0, 1, 2, 3, 4, 5};

- T = {a, b};

- S = 5;

- P‟ : 5 4  2; 4  b3; 3  b3  b0  0; 2  a2 a1 b1; 1 0; 0  a0.

- Xây dựng văn phạm tuyến tính trái G đảo ngược của G‟ và tương đương với M2.

G = (N, T, P, S):

- N = {0, 1, 2, 3, 4, 5};

- T = {a, b};

- S = 5;

- P : 5 4  2; 4  3b; 3  3b  0b  0; 2  2a 1a 1b; 1 0; 0  0a.

e) Biểu thức chính quy tương đương với M2.

Từ đồ thị suy ra biểu thức chính quy r2 = a* ((a  b) a* (b ) b+)

2.34. 1) Xây dựng văn phạm tuyến tính phải tương đương với mỗi FA a) Ta có M1 = <Q, , , q0, F>:

- Q = {0, 1, 2, 3};

-  = {a, b};

- q0 = 0 ;

- F = {3};

Từ đó, ta có G = (N, T, P, S):

- N = {0, 1, 2, 3};

- T = {a, b};

- P :

0  a0  a1 b1; 1  a2  b2; 2  a2 a3 a; 3  a3 a 3 0 b3 b;

- S = 0.

b) Ta có M2 = <Q, , , q0, F>:

- Q = {0, 1, 2, 3};

-  = {a, b};

- q0 = 0 ;

- F = {3};

Từ đó, ta có G = (N, T, P, S):

- N = {0, 1, 2, 3};

- T = {a, b};

- P :

0  a1  a3 a  b1 1; 1  a2  b1 b2; 2  a3 a 3;

- S = 0.

2) Xây dựng văn phạm tuyến tính trái tương đương với mỗi FA trên.

a) - Xây dựng văn phạm tuyến tính trái G = (N, T, P, S) tương ứng với M như

+ Từ FA M có FA M‟ = <Q, , ‟, q‟0, F‟> đảo ngược: q‟0 = 3 ;

F‟ = {0};

‟:

Q 

a	b	
0	{0}		{3}
1	{0}	{0}
2	{1; 2}	{1}
3	{2; 3}	{3}

+ Văn phạm tuyến tính phải tương ứng với M‟:

N‟ = {3, 2, 1, 0}; T‟ = {a, b}; S‟ = 3 ;

P‟: 0  a0 a 3; 1 a0 a b0 b; 2  a1 a2 b1;

3  a2 a3b3.

+ Văn phạm tuyến tính trái tương ứng với:

N = {3, 2, 1, 0}; T = {0, 1}; S = 3 ;

P‟: 0  0a a 3;

1 0a a 0b b; 2  1a 2a 1b;

3  2a 3a3b.

Đặt 3 = S ; 2 = A; 1 = B; 0 = C . Ta có:

P: S  Sa Sb Aa; A  Aa  Ba Bb;

B  Ca a  Cb b; C  Ca a  S.

b) Tương tự (tự làm)

3) Tìm biểu thức chính quy tương đương với mỗi NFA trên.

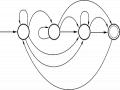
a) - Biểu diễn M dưới dạng đồ thị

Start



a a a

- Từ đồ thị suy ra biểu thức chính quy r = ( a* (a  b)( a  b) a*a( a  b)*)+

= ( a* (a  b)( a  b) a+( a  b)*)+

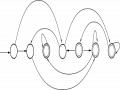
b) - Biểu diễn M dưới dạng đồ thị

Start



b

- Từ đồ thị suy ra biểu thức chính quy r = ((a b ) b* (a b )(a))  a

2.35. 1) Xây dựng văn phạm tuyến tính phải tương đương với NFA trên. Từ đồ thị suy ra M = <Q, , , q0, F>:

- Q = {A, B, C, D};

-  = {0, 1};

- q0 = A ;

- F = {D};

- :

 1

 0C 1BC

C 1DCA

DA

Từ đó, ta có G = (N, T, P, S):

- N = {A, B, C, D};

- T = {0, 1};

- P :

A  1A  1B; B  0C  1B  C; C  1D 1 A; D  A;

- S = A.

2) Xây dựng văn phạm tuyến tính trái tương đương với NFA trên. Tương tự bài 2.34, câu 2a.

- Xây dựng M‟ đảo ngược của M;

- Xây dựng văn phạm tuyến tính phải G‟ tương ứng với M‟;

- Xây dựng văn phạm tuyến tính trái G đảo ngược của G‟.

3) Tìm biểu thức chính quy tương đương với NFA trên r = ( (1*11*(0 ) ) + 1) +

= ( (1+(0 ) ) + 1) +

2.36. 1) Xây dựng các NFA đoán nhận các ngôn ngữ được biểu diễn bởi mỗi biểu thức:

a) r = 0 (1 + 2) 3*

1. Phân tích

- Ta có r = r1r2; r1= 0 (1 + 2); r2= 3*

- r1 = r3 r4; r3 = 0; r4 = 1 + 2

- r4 = r5 + r6 ; r5= 1; r6 = 2

- r2= (r7 ) *; r7= 3.

2. Xây dựng r

- Xây dựng r3 = 0; r5= 1; r6 = 2; r7 = 3

- Xây dựng r4 = r5 + r6

- Xây dựng r1 = r3 r4

- Xây dựng r2= (r7 ) *

- Xây dựng r = r1r2 b) 0 (1+ 2 + 3)+

1. Phân tích

- Ta có r = r1r2; r1= 0; r2= (1+ 2 + 3)+

- r2 = (r3 ) + ; r3= 1+ 2 + 3

- r3 = r4+ r5 ; r4 = 1 + 2; r5 = 3

- r4 = r6 + r7 ; r6= 1; r7 = 2

2. Xây dựng r

- Xây dựng r1 = 0; r5= 3; r6 = 1; r7 = 2

- Xây dựng r4 = r6 + r7

- Xây dựng r3 = r4+ r5

- Xây dựng r2 = (r3 ) +

- Xây dựng r = r1r2 c) (0 + 1)* + (23)+

1. Phân tích

- Ta có r = r1+ r2; r1= (0 + 1)*; r2= (23)+

- r1 = (r3 ) *; r3 = 0 + 1

- r3= r4 + r5 ; r4= 0; r5 = 1

- r2= (r6 ) + ; r6= 23

- r6= r7 r8 ; r7= 2; r8 = 3

2. Xây dựng r

- Xây dựng r4 = 0; r5= 1

- Xây dựng r3= r4 + r5

- Xây dựng r1 = (r3 ) *

- Xây dựng r7 = 2; r8 = 3

- Xây dựng r = r r

6 7 8

- Xây dựng r = (r ) +

2 6

2) Xây dựng văn phạm chính quy cho các ngôn ngữ được biểu diễn bởi mỗi biểu thức.

Áp dụng giải thuật xây dựng văn phạm chính quy khi biết automat hữu hạn cho mỗi automat (tương tự bài 2.35)

2.37. 1) G = (N, T, P, S):

- N= {A, B, C};

- T = {0, 1};

- P = {A → 0A| 0B| 1C | ε; B → 0C| 1A; C → 0B| 1C| 0 | 1};

- S = A.

2) M = <Q, , , q0, F>:

- Q = {A, B, C, D};

-  = {0, 1};

- :

+  (A, 0) = {A, B} vì A → 0A| 0B P;

+  (A, 1) = {C} vì A → 1C  P;

+  (A, ε) = {D} vì A → ε  P;

+  (B, 0) = {C} vì B → 0C  P;

+  (B, 1) = {A} vì B → 1A  P;

+  (C, 0) = {B, D} vì C → 0B| 0 P;

+  (C, 1) = {C, D} vì C → 1C| 1 P;

- q0 = A;

- F = {D} vì A → ε  P.

3) Biểu diễn M bằng đồ thị

Start

