Giá Trị Và Thời Điểm Xuất Hiện Lượng Mưa Ngày Lớn Đột Biến (Hngàymax)* Trong Chuỗi Số Liệu Từ Năm 1960 – 2010 Tại 12 Trạm Khí Tượng Chọn

y

./ Bước 1: bằng phương pháp mô men, sử dụng các công thức (2.1), (2.2), (2.4) để ước tính giá trị các tham số thống kêX, Cv, Cs của chuỗi số liệu lượng mưa

ngày lớn nhất năm H

ngà max.

./ Bước 2: tính và vẽ đường tần suất lý luận với các tham số thống kêX, Cv, Cs vừa tính ở bước 1.

n

1 . n [ X X ]2

2

i

i1

1 C 2

v

6

n

.(1 6C  5C )

2

4

v

v

./ Bước 3: kiểm tra, hiệu chỉnh. Khi đường tần suất lý luận vẽ ở bước 2 thấy chưa phù hợp với các điểm tần suất kinh nghiệm, cần hiệu chỉnh lại giá trị các tham sốX, Cv, Cs, thường trong phạm vi sai số tuyệt đối của nó (X Xtb), (Cv Cv),

(C 

) với  

,  

Cv .

,  

s Cs

Xtb

Cv Cs

2n

và vẽ lại đường tần suất lý luận với các giá trịX, Cv, Cs vừa hiệu chỉnh. Cứ tiến hành thử dần như vậy cho đến khi tìm được đường tần suất lý luận phù hợp nhất với các điểm tần suất kinh nghiệm thì dừng lại. Đường tần suất lý luận phù hợp tìm được phải là một đường cong trơn, cong một chiều, không tồn tại những điểm gẫy và đi qua trung tâm các điểm tần suất kinh nghiệm.

./ Việc tính và vẽ ở bước 1, bước 2 trong luận án được hỗ trợ bởi phần mềm tính và vẽ đường tần suất FFC2008 [58], TSTV2002 [57].

+) Giá trị lượng mưa ngày tính toán Hn,p ở tần suất p tính theo công thức (3.5) sau.

H n, p K p .X

(3.5)

với:X là giá trị trung bình ứng với đường tần suất lý luận phù hợp tìm được của lượng mưa ngày lớn nhất năm

Kp là hệ số mô đuyn ở tần suất p của đường tần suất lý luận phù hợp tìm được, tra bảng toán học lập sẵn, phụ thuộc vào luật phân bố, hệ số Cv, Cs của đường tần suất lý luận phù hợp tìm được và tần suất p%, xem trong các tài liệu [3], [14], [15], [36], [45], . . . Bảng tra Kp này cũng được cập nhật trong [57], [58].

3.1.2.4. Xử lý khi gặp những trận mưa đặc biệt lớn.

+) Đây là vấn đề mới nảy sinh trong chuỗi số liệu đo lượng mưa ngày lớn nhất năm Hngàymax ở nước ta quan trắc đến thời điểm hiện nay, do ảnh hưởng của hiện tượng BĐKH nên trong những năm càng về gần đây có xuất hiện các giá trị lượng mưa ngày lớn đột biến (Hngàymax)*. Để bảo đảm kết quả tính toán xác định Hn,p theo tần suất là chính xác, khi gặp các giá trị (Hngàymax)* lớn đột biến trong chuỗi số liệu quan trắc

max

max *

+) Bảng 3.2 dưới đây là thống kê giá trị và thời điểm xuất hiện các giá trị (Hngày ) lớn đột biến trong chuỗi số liệu Hngày quan trắc ở 12 trạm khí tượng, thời kỳ từ năm

1960 -2010, như nghiên cứu đã chỉ ra của chương 2. Nhằm làm rõ hơn, trong bảng có

ngày

ngay

so sánh các giá trị (H max)*lớn đột biến này với trị số H max  3. và nhận thấy

chúng đều lớn hơn. Ở đây,  là độ lệch chuẩn của chuỗi số liệu thống kê lượng mưa

1 .

n

n  1

[(H max ) H max ]2

ngay i ngay

i 1

ngày lớn nhất năm,  . Như vậy, trừ ba trạm TX.Mường

Lay, TP.Nha Trang, TP.Cần Thơ, có đến 9/12 trạm khí tượng nghiên cứu phải xử lý mưa đặc biệt lớn theo trường hợp ở Hình 3.2, Hình 3.3 và công thức (3.6) dưới đây.

Cũng nhìn vào Bảng 3.2 nhận thấy trong thời kỳ từ năm 1960 - 2010, các giá trị

(Hngày

max)* lớn đột biến đều xảy ra vào những năm càng về gần đây.

Bảng 3.2: Giá trị và thời điểm xuất hiện lượng mưa ngày lớn đột biến (Hngàymax)* trong chuỗi số liệu từ năm 1960 – 2010 tại 12 trạm khí tượng chọn nghiên cứu

TT

Trạm, địa danh	Thời kỳ quan trắc	Hngàymax (mm)	Độ lệch chuẩn  (mm)	Giá trị Hngàymax+3 (mm)	Giá trị (Hngàymax)* (mm)	Thời điểm xuất hiện (Hngàymax)* lớn đột biến	Năm lịch sử biết được
1	Thị xã Mường Lay	1960 - 2010	133.11	43.93	264.89	-	0/ có	1960
2	TP. Tuyên Quang	1960 - 2010	123.11	46.78	263.46	316.0	17/ 7 / 2006	1960
3	TP. Lạng Sơn	1956 - 2010	105.95	32.84	204.48	215.2	26/ 9 / 2008	1956
4	Láng - TP.Hà Nội	1956 - 2010	137.1	58.95	313.96	394.9 347.0	10/ 11 / 1984, 31/ 10 / 2008	1956
5	Hà Đông - Hà Nội	1960 - 2010	137.55	75.65	364.51	514.2	31/ 10 / 2008	1960
6	TX.Sơn Tây - HN	1960 - 2010	145.79	78.73	381.97	508.0	14/ 7 / 1971	1960
7	TP. Vinh	1960 - 2010	232.15	99.82	531.62	596.7	11/ 10 / 1989	1960
8	TP. Đồng Hới	1956 - 2010	237.46	87.86	501.04	554.6	09/ 10 / 1995	1956
9	TP. Đà Nẵng	1980 - 2010	232.17	99.83	531.67	592.6	03/ 11 / 1999	1980
10	TP. Nha Trang	1980 - 2010	156.4	68.82	362.85	-	0/ có	1980
11	TP. B - Ma Thuột	1977 - 2010	117.2	50.40	268.39	285.6	28/ 6 / 2006	1977
12	TP. Cần Thơ	1980 - 2010	89.31	21.43	153.61	-	0/ có	1980

Có thể bạn quan tâm!

• Giá Trị Trung Bình Trong Nhiều NămX Và Hệ Số Cv, Cs Của Lượng Mưa Ngày Lớn Nhất Năm Hngàymax Và Cường Độ Mưa Thời Đoạn Tính Toán Lớn Nhất Năm
• Chu Kỳ Biến Đổi Của Lượng Mưa Ngày Lớn Nhất Năm Hngàymax Tại Trạm Láng - Tp.hà Nội Từ Năm 1960 – 2010
• Xác Định Lượng Mưa Ngày Tính Toán Theo Tần Suất Thiết Kế Hn,p.
• Phương Pháp Xây Dựng Hàm Hệ Số Đặc Trưng Hình Dạng Cơn Mưa T Theo T
• Khái Niệm: Cường Độ Mưa Là Lượng Mưa Trong Một Đơn Vị Thời Gian, Thường Ký Hiệu Là A, Đơn Vị Tính Thường Tính Là Mm/phút. Cường Độ Mưa Là Một
• Nghiên Cứu Xác Định Cường Độ Mưa Tính Toán At,p Dựa Vào Lượng Mưa Ngày Tính Toán Hn,p Và Hệ Số Đặc Trưng Hình Dạng Cơn Mưa T.

Xem toàn bộ 160 trang tài liệu này.

Chú ý: trong bảng các giá trị (Hngàymax)* là các giá trị mưa lớn đột biến, không phải sai số thô vì ở các trạm khí tượng sai số thô (nếu có) đã được theo dõi, loại bỏ theo quy trình thu thập, chính lý số liệu khí hậu (ví dụ như theo dõi cả giờ, ngày, tháng, ghi chú các hiện tượng thời tiết đặc biệt, đo đối chứng đồng thời bằng nhiều máy, . . .)

+) Việc xử lý mưa đặc biệt lớn (ĐBL) như sau: tần suất kinh nghiệm p của các giá trị tham số mưa Hngàymax thông thường vẫn được tính theo công thức (3.4) với các chỉ số k và n là của giá trị tham số mưa thông thường, còn tần suất kinh nghiệm của các giá trị tham số mưa (Hngàymax)* đặc biệt lớn phải được hiệu chỉnh theo công thức (3.6) sau.

p M N  1

.100

(3.6)

max *

Trong đó: M là số thứ tự của giá trị tham số mưa (Hngày ) đặc biệt lớn trong liệt thứ tự số liệu xắp xếp theo giá trị giảm dần

N là thời kỳ xuất hiện lại của mưa đặc biệt lớn, xác định theo các trường hợp như ở hình 3.2, hình 3.3 sau đây, [3], [15], [35], [36].

Năm lịch sử biết được A0 trùng với năm bắt đầu

quan trắc

N = A - A0 (năm)

M=1

N1 = (A - A0), N2 = (A - A0)/2 (năm)

Năm tính toán hiện tại A

Năm lịch sử biết được A0 trùng với năm bắt đầu

quan trắc

Năm tính toán hiện tại A

M=1

M=2

n

Chuỗi thống kê

n

Chuỗi thống kê

Mưa ĐBL có thứ tự M=1, N = (A – A0)

Hình 3.2: Trường hợp có 1 cơn mưa ĐBL nằm trong chuỗi số liệu thống kê

(Mưa ĐBL thứ tự M=1) > (Mưa ĐBL M=2) Mưa ĐBL có thứ tự M=1, N1 = (A – A0) Mưa ĐBL có thứ tự M=2, N2 = (A – A0)/2 Hình 3.3: Trường hợp có nhiều cơn mưa

ĐBL nằm trong chuỗi số liệu thống kê

Năm lịch sử A0 là năm biết được qua điều tra hoặc đo đạc trong quá khứ. Đối với chuỗi số liệu quan trắc Hngàymax tại các trạm đo mưa ở nước ta thì năm lịch sử biết được A0 thường là năm bắt đầu tiến hành công việc quan trắc đo lượng mưa ngày tại trạm khí tượng đó, và chuỗi số liệu thống kê Hngàymax thu thập đưa vào tính toán tìm Hn,p cũng thường bắt đầu từ đây. Do vậy các giá trị M, N, n, k sẽ được xác định như ở các Hình 3.2, Hình 3.3 cho trường hợp có 1 trận mưa hoặc nhiều trận mưa đặc biệt lớn nằm trong chuỗi số liệu thống kê. Trường hợp ở hình 3.3, theo định nghĩa trong

[15] thì thời kỳ xuất hiện lại của mưa ĐBL là số năm trung bình để xảy ra trận mưa lớn hơn hoặc bằng trận mưa ĐBL có giá trị lớn nhất (trong số các trận mưa ĐBL) do vậy lấy N bằng N1 để tính toán.

Ghi chú: Trong trường hợp có xuất hiện các giá trị mưa đặc biệt lớn trong chuỗi số liệu thống kê lượng mưa ngày lớn nhất năm như các trường hợp ở hình 3.2, hình 3.3

thì các công thức (2.1), (2.2) dùng ước tính các tham số thống kêX, Cv bằng phương pháp mô men phải được hiệu chỉnh lại như sau đây:

N

1 M * N M

nM 

Công thức (2.1) tínhX được hiệu chỉnh thành:

X X j 

n M

.X i 

Công thức (2.2) được hiệu chỉnh: Cv 

j 1

i 1 

1M

N 1 (K j

1)

2 N MnM

j 1

n M

. (K 1) 



2 

i

i 1



Công thức (2.4) tính hệ số Cs giữ nguyên không hiệu chỉnh

X *

j

j

Với: Kj là hệ số biến xuất của mưa đặc biệt lớn X *,

K j 

X

Ki là hệ số biến xuất của mưa thường Xi ,

K X i

iX

Khi tính Kj, Kithì giá trịX đã được hiệu chỉnh mưa ĐBL.

3.1.2.5. Kiểm định sự phù hợp của đường tần suất lý luận Hn,p với tài liệu thực đo.

+) Khi vẽ thử dần tìm vị trí phù hợp của đường tần suất lý luận với các điểm tần suất kinh nghiệm thực ra là ta đã thực hiện kiểm định sự phù hợp của đường tần suất lý luận với số liệu thực đo, nhưng việc so sánh bằng mắt còn mang tính chủ quan, cần có phương pháp khách quan hơn để đánh giá. Luận án sử dụng tiêu chuẩn Smirnov - Kolmogorov để kiểm định sự phù hợp của đường tần suất lý luận với số liệu thực đo.

+) Tiêu chuẩn kiểm định Smirnov - Kolmogorov: đường tần suất lý luận được coi là phù hợp với số liệu đo thực tế ở mức ý nghĩa  khi thỏa mãn điều kiện (3.7) sau.

D th

(%) (3.7)

Trong đó: th là giá trị tới hạn ứng với mức ý nghĩa  cho phép. Trong tính toán khí tượng thủy văn thường chọn mức ý nghĩa cho phép  =5%, theo [6], [14], [36], [43], có nghĩa độ tin cậy của kết quả tính toán kiểm định là Rtincậy = 1 -  = 95%. Giá trị th được tra Bảng PL.10-1 ở phụ lục 10 phụ thuộc vào số lượng mẫu n và mức ý nghĩa  cho phép.

D là chênh lệch lớn nhất giữa đường tần suất lý luận và kinh nghiệm.

X

D  max P'

PX

(3.8)

với: PX là giá trị tần suất lý luận ứng với giá trị bằng X của lượng mưa ngày tính toán Hn,p

PX’ là giá trị tần suất kinh nghiệm ứng với giá trị cũng bằng X của

lượng mưa ngày lớn nhất năm thực đo Hngàymax.

Hngày

+) Bảng 3.3 dưới đây là kết quả kiểm định sự phù hợp của đường tần suất lý luận lượng mưa ngày tính toán Hn,p so với tài liệu đo thực tế lượng mưa ngày lớn nhất năm max, ở 12 trạm khí tượng nghiên cứu, từ năm 1960 – 2010. Nhận thấy chúng đều

thỏa mãn, đạt được độ tin cậy Rtincậy  95%.

Bảng 3.3: Kết quả kiểm định theo tiêu chuẩn Smirnov – Kolmogorov về sự phù hợp với số liệu thực đo của đường tần suất lý luận lượng mưa ngày tính toán Hn,p tại 12 trạm khí tượng chọn nghiên cứu với mức ý nghĩa cho phép  = 5%

STT

Trạm, địa danh	Thời kỳ đo mưa	Số năm thống kê n	Giá trị tới hạn th,=5%	Chênh lệch lớn nhất D	Đánh giá
1	Thị xã Mường Lay	1960 - 2010	51	18.89%	8.00%	Đạt
2	TP. Tuyên Quang	1960 - 2010	51	18.89%	8.00%	Đạt
3	TP. Lạng Sơn	1956 - 2010	55	18.34%	6.40%	Đạt
4	Láng - TP.Hà Nội	1956 - 2010	55	18.34%	9.20%	Đạt
5	Hà Đông - Hà Nội	1960 - 2010	51	18.89%	3.00%	Đạt
6	TX.Sơn Tây - HN	1960 - 2010	51	18.89%	1.60%	Đạt
7	TP. Vinh	1960 - 2010	51	18.89%	7.00%	Đạt
8	TP. Đồng Hới	1956 - 2010	55	18.34%	12.00%	Đạt
9	TP. Đà Nẵng	1980 - 2010	31	23.70%	11.10%	Đạt
10	TP. Nha Trang	1980 - 2010	31	23.70%	9.20%	Đạt
11	TP. Buôn Ma Thuột	1977 - 2010	34	22.80%	5.80%	Đạt
12	TP. Cần Thơ	1980 - 2010	31	23.70%	9.10%	Đạt

3.1.3. Kết quả xác định lượng mưa ngày tính toán Hn,p theo tần suất thiết kế p ở 12 trạm khí tượng nghiên cứu lập với chuỗi số liệu đo mưa thực tế từ 1960 - 2010.

- Để rút ngắn thời gian và nâng cao mức độ chính xác đã sử dụng phần mềm FFC2008 [58], TSTV2002 [57] để hỗ trợ trong việc tính và vẽ đường tần suất, [58] dùng tính và vẽ, [57] dùng tính đối chứng. Tuy nhiên việc sử dụng các phần mềm này trong luận án chỉ hỗ trợ được một bước công việc trong sơ đồ tính rất nhiều bước ở Hình 3.1, các phần mềm này hỗ trợ việc tự động tính và vẽ đường tần suất lý luận trong khâu tìm đường tần suất lý luận phù hợp như đã được chỉ ra trong mục 3.1.2.3 ở trên.

- Kết quả xác định lượng mưa ngày tính toán Hn,p theo tần suất p ở 12 trạm khí tượng nghiên cứu lập với chuỗi số liệu đo mưa thực tế từ năm 1960 - 2010 được lập thành đồ thị tra và bảng tra như trong Phụ lục 1: các Đồ thị PL.1-1, PL.1-2, PL.1-3, PL.1-4, PL.1-5, PL.1-6, PL.1-7, PL.1-8, PL.1-9, PL.1-10, PL.1-11, PL.1-12 và Bảng PL.1-13.

3.1.4. So sánh lượng mưa ngày tính toán Hn,p theo tần suất thiết kế p tính từ năm 1960 tới năm 2010 so với Hn,p tính tới năm 1987 lập trong [5]. Nhận xét, kiến nghị.

- Kết quả so sánh giá trị lượng mưa ngày tính toán Hn,p xác định với chuỗi số liệu đo mưa thực tế từ năm 1960 đến năm 2010 ở 12 trạm khí tượng chọn nghiên cứu với giá trị lượng mưa ngày tính toán Hn,p xác định với chuỗi số liệu đo mưa thực tế đến năm 1987 đã lập trong [5] như ở Bảng của Phụ lục 12 Quyển phụ lục luận án.

- Luận án có nhận xét và kiến nghị.

+) Sau trên 23 năm, từ năm 1987  2010, ở tất cả các trạm khí tượng chọn nghiên cứu ở các vùng miền trên toàn quốc (12 trạm), giá trị lượng mưa ngày tính toán Hn,p ở các tần suất p thay đổi rất nhiều. Ở các mức tần suất p càng nhỏ thì sự thay đổi thường càng lớn, có khi tăng lên gấp 1.5 - 2 lần, ở mức tần suất p càng lớn thì sự chênh lệch ít hơn. Kết qủa so sánh ở Bảng tại Phụ lục 12 quyển phụ lục luận án hoàn toàn phù hợp với các nghiên cứu về quy luật biến đổi của chế độ mưa tại các trạm khí tượng chọn nghiên cứu đã thực hiện ở chương 2, đó là chế độ mưa ở nước ta đã có sự thay đổi và thay đổi đáng kể những năm càng về gần đây.

+) Kiến nghị sử dụng các số liệu lượng mưa ngày tính toán Hn,p theo tần suất p lập với số liệu đo mưa thực tế từ năm 1960 - 2010 (khoảng thời gian cuối ứng với bối cảnh BĐKH) ở vị trí 12 trạm khí tượng nghiên cứu như trong Phụ lục 1 quyển phụ lục luận án, tính ở các mức tần suất p = 1%  99.99%, để tính toán lưu lượng đỉnh lũ thiết kế công trình thoát nước trên đường tại những khu vực có các trạm khí tượng này.

3.2. Nghiên cứu xác định hệ số đặc trưng hình dạng cơn mưa T và đề xuất tiêu chí phân vùng mưa phù hợp đối với yêu cầu tính toán lưu lượng lũ lưu vực nhỏ của công trình thoát nước nhỏ trên đường.

3.2.1. Khái niệm và đặc tính của hàm hệ số đặc trưng hình dạng cơn mưa .

- Gọi T,p là hệ số đặc trưng hình dạng cơn mưa ở thời đoạn T và tần suất p tại một vùng mưa nào đó, thì:

T , p

HT , p

H

(3.9)

n, p

với: HT,p là lượng mưa lớn nhất trong thời đoạn tính toán T ở tần suất p hay còn gọi là lượng mưa tính toán ở thời đoạn T và tần suất p

Hn,p là lượng mưa ngày tính toán ở tần suất p T là thời đoạn mưa tính toán.

- Theo biểu thức (3.9), có nhận định về mặt lý luận như sau: giá trị ở tử số là lượng mưa tính toán thời đoạn HT,p và giá trị ở mẫu số là lượng mưa ngày tính toán Hn,p đều

phụ thuộc vào cùng một tần suất p như nhau, như vậy theo phân tích lôgic thì đại lượng T,p sẽ chỉ còn phụ thuộc vào thời đoạn mưa tính toán T mà không còn hoặc còn rất ít phụ thuộc vào tần suất p nữa. Tuy nhiên giả thiết này cũng cần được kiểm tra, đánh giá qua các tài liệu đo mưa thực tế ở các trạm khí tượng.

- Các kết quả nghiên cứu trên nhiều số liệu đo mưa thực tế (VD như được giới thiệu tại các hình ở Phụ lục 13 quyển phụ lục luận án và kết quả đánh giá sai số ở Bảng 3.5 thể hiện mức độ không phụ thuộc vào tần suất p tại 12 trạm nghiên cứu) chỉ ra rằng.

+) Trong một vùng mưa đã được xác định (vùng thiết kế) thì họ các đường cong quan hệ T,p  T ở các tần suất p khác nhau rất sít nhau, có nghĩa có thể xem như chúng không phụ thuộc vào tần suất p nữa, như ở Hình 3.4. Bởi vậy, lấy đường trung bình của họ các đường cong T,p  T ở các tần suất p để đại diện cho vùng mưa đó, đường trung bình này được ký hiệu là T , như vậy T chỉ còn phụ thuộc vào T, không phụ thuộc vào p, hàm quan hệ T  T như ở Hình 3.5.

Ta có:

H T , p

(3.10)

H

T

n, p

Trong đó: T là hệ số đặc trưng hình dạng cơn mưa của vùng, không phụ thuộc vào p, chỉ phụ thuộc vào thời đoạn tính toán T

HT,p là lượng mưa tính toán ở thời đoạn T và tần suất p Hn,p là lượng mưa ngày tính toán ở tần suất p.

1 2

...

p

1 2

...

p

1

.2..

p

tb T

tb T

tb T

Vïng 1

Vïng 2

Vïng 1

Vïng 2

T,p T

Vïng 3

Vïng 3

0 T

Hình 3.4: Họ đường cong T,p  T ít thay đổi theo tần suất trong một vùng mưa nhưng khác nhau giữa các vùng mưa

0 T

Hình 3.5: Phân vùng mưa bằng đường cong hệ số đặc trưng hình dạng cơn mưa T  T

+) Hàm T có tính vùng rõ rệt: ở các vùng mưa khác nhau thì đường cong quan hệ

T  T sẽ khác nhau. Do vậy sử dụng đường quan hệ T  T để phân vùng mưa.

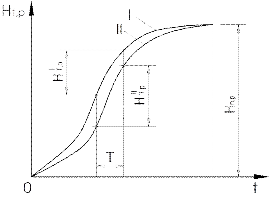
- Ý nghĩa của hệ số T: Xét lại cơn mưa tính toán ở Hình 1.4 chương 1, ở hai vùng mưa I và II khác nhau, mặc dù có cùng lượng mưa ngày tính toán Hn,p nhưng nếu hình dạng cơn mưa khác nhau, thì.

+) Cường độ mưa tính toán aT,p ở thời đoạn T và tần suất p phụ thuộc vào lượng mưa HT,p lớn nhất của thời đoạn tính toán T ở tần suất p, aT,p = HT,p / T.

+) Với cùng một thời đoạn tính toán T

I II I II

và tần suất p thì lượng mưa tính toán thời đoạn HT,p sẽ khác nhau ở các vùng

mưa do ảnh hưởng của hình dạng cơn mưa, HT,p  HT,p nên (HT,p /T)  (HT,p /T), tức

I II

cường độ mưa tính toán aT,p  aT,p .

+) Như vậy, đặc trưng cho hình dạng cơn mưa có thể được biểu diễn bằng tỷ số giữa lượng mưa lớn nhất trong thời đoạn tính toán HT,p và lượng mưa ngày tính toán Hn,p (tỷ số HT,p / Hn,p). Do vậy T được gọi là hệ số đặc trưng hình dạng cơn mưa.

- Từ phân tích trên có nhận xét.

./ Trong một vùng mưa đã được xác định thì lượng mưa ngày tính toán Hn,p chỉ phụ thuộc vào tần suất thiết kế p, không phụ thuộc vào hình dạng cơn mưa.

./ Còn cường độ mưa tính toán aT,p ngoài việc phụ thuộc vào tần suất thiết kế p, thời đoạn mưa tính toán T còn phụ thuộc vào hình dạng cơn mưa.

3.2.2. Mục đích, ý nghĩa của việc nghiên cứu xác định hệ số đặc trưng hình dạng cơn mưa T.

- Trong mục 3.1 đã nghiên cứu hoàn chỉnh việc xác định lượng mưa ngày tính toán Hn,p

theo tần suất với số liệu đo mưa thực tế liên tục từ năm 1960 - 2010, cập nhật được các diễn biến thời tiết đến thời điểm hiện nay ở nước ta. Trong tính toán lưu lượng thiết kế công trình thoát nhỏ trên đường ở nước ta hiện nay đang dùng tiêu chuẩn TCVN9845:2013 [5], sử dụng công thức cường độ giới hạn tính theo lượng mưa ngày tính toán, công thức (1.9). Trong công thức này đã sử dụng công thức (1.14) để xác

định cường độ mưa tính toán: a

T , p

T .H T

n, p

, khi tính toán lấy T = .

Như vậy, để xác định được lưu lượng thiết kế công trình thoát nước nhỏ trên đường Qp theo công thức (1.9) như trong [5] thì ngoài việc xác định được thông số