Mô Hình Cháy Không Đồng Nhất Thông Qua Đại Lượng Bảo Toàn

thang độ rối cần thiết nhất, đặc biệt là năng lượng rối. Trong những mô hình này, mô hình k- được sử dụng nhiều nhất.

Mô hình k- dùng hai phương trình chuyển phụ, trong đó một phương trình biểu diễn năng lượng rối k và phương trình còn lại biểu diễn tốc độ tiêu tán đại lượng này . Hai phương trình này được viết dưới dạng thông thường sau đây:

k k 1 v k U 2

U . V rvt. vt 

x r r r kr r 

(2.22)

l v U 22

U . V rvt. cl vt c2

x r r r r k r k

(2.23)

Có thể bạn quan tâm!

Xem toàn bộ 178 trang tài liệu này.

Trong đó:

v c . k 2

t 

(2.24)

Mô hình này được sử dụng rộng rãi trong ngọn lửa rối. Tuy nhiên, mô hình k-

 không cho kết quả chính xác trong tính toán dòng chảy elip, chẳng hạn trong vùng có sự chuyển động xoáy ngược. Mô hình về sự khép kín Reynolds [40], [41], [42], cho kết quả tốt hơn trong trường hợp đó, nhưng không cho kết quả tốt trong trường hợp tổng quát. Sự so sánh hai mô hình được đề cập trong [40], [43]. Trong mọi trường hợp, mô hình k- không ảnh hưởng mạnh mẽ đến kết quả tính vì sự xoáy ngược của dòng chảy được khống chế chủ yếu bằng hiện tượng đối lưu [44].

Sự gia tăng độ nhớt do nhiệt độ tăng làm triệt tiêu hiện tượng rối ở một số vùng, đặc biệt là vùng gần vòi phun. Hiện tượng đó gọi là chảy tầng hóa do quá trình cháy được đề cập trong [45]. Cơ chế của hiện tượng này có thể giải thích bởi sự gia tăng độ nhớt làm giảm số Reynolds rối cục bộ. Cân bằng giữa đại lượng sản sinh và tiêu tán năng lượng rối bị phá vỡ. Quá trình rối vì vậy bị mất đi.

Hiện tượng này đồng thời có ảnh hưởng quan trọng đến vùng có chuyển động ngược của dòng chảy trong màng lửa.

Khi kể đến hiện tượng này, mô hình quá trình rối phải thay đổi cho phù hợp.

Mô hình k- vì vậy được viết:

k k 1 v k U 2

U .V . rvt. vt 

x r r r k r r 

2

1 v U 2

U . V . rvt. cl vt cf

x r r r r k r k

2 2

(2.25)

Trong đó:

k 2

vt c. f

(2.26)

Tóm lại, Hệ phương trình viết theo đại lượng trung bình kiểu Favre và xấp xỉ lớp biên (2.13) – (2.16) được sử dụng trong công trình này. Mô hình k- thường được biểu diễn bởi các chương trình (2.22), (2.23) phù hợp với việc mô tả dòng chảy rối trong xi lanh và buồng cháy động cơ đánh lửa cưỡng bức.

2.2. Mô hình cháy không đồng nhất

2.2.1. Các mô hình cháy không đồng nhất

Việc tính toán môi trường đang diễn ra phản ứng hóa học khó khăn hơn rất nhiều so với môi trường khí trơ do sự thay đổi nồng độ các chất và năng lượng cháy tỏa ra. Việc tính toán các chi tiết cần phải biết động học của mỗi phản ứng cơ sở. Tổng quát hóa một mô hình động học phản ứng cho toàn bộ các phản ứng hóa học trong hệ thống hầu như không thực hiện được.

Việc phát triển mô phỏng toán học về quá trình cháy cho phép thiết lập một mô hình tổng quát cho nhiều hệ thống cháy khác nhau.

Trước năm 1970, mô hình toán học phát triển theo chiều hướng này không đề cập đến sự dao động nồng độ [46]. Mặc dù vậy, dạng mô hình đó cũng đã rất có ích trong tính toán thực tế.

Howe và các đồng sự [47] (1965) đã đề nghị một mô hình cho tốc độ cháy gọi là “tentative model”. Vùng phản ứng được đặc trưng bởi những mô hình bọc khí chưa cháy phân tán trong không khí khi nồng độ thể tích của khí cháy lớn hơn 0,5. Trong trường hợp ngược lại, nếu nồng độ thể tích của khí chưa cháy lớn hơn 0,5; khí cháy được xem như phân bố trong khí chưa cháy. Vấn đề trung tâm của mô hình “tentative

model” là thiết lập một hàm phân bố các bọc khí chưa cháy, về cả số lượng lẫn kích thước, trong hỗn hợp với khí cháy để xác định tốc độ phản ứng.

Trong những năm 70, Spalding đã giới thiệu mô hình “eddy-break-up” [48], [49]. Cơ sở của mô hình này là đưa vào khái niệm “tính phản ứng” được định nghĩa bởi:

mfu mfu,u

mfu,b mfu,u

(2.27)

mfu là nồng độ khối lượng của nhiên liệu, các chỉ u; b lần lượt chỉ khí chưa cháy và khí cháy.

Nếu chúng ta cho rằng hỗn hợp chỉ chứa khí cháy hoàn toàn và khí chưa cháy,



số trung bình thời gian τ, là phần thời gian tồn tại của khí mà “tính phản ứng” cao nhất.

Tốc độ cháy phụ thuộc vào cả đại lượng τ lẫn tốc độ phá vỡ những cấu trúc lớn thành những cấu trúc nhỏ đủ để cho quá trình truyền nhiệt và phản ứng hóa học trở nên đáng kể. Tốc độ phá vỡ cấu trúc này tỉ lệ với gradient vận tốc.

Tốc độ cháy Rf được cho bởi [48]:

1

-U 1 

R (m ) 1 C( 1).

f f ,max x f

i

(2.28)

+ Trong đó m là tốc độ phản ứng cực đại, C= 0,35 là một hằng số, ρ là khối lượng riêng của chất khí.

Mô hình “eddy dissipation” của Magnussen [50], [51] được thiết lập dựa trên cùng một nguyên tắc với mô hình “eddy-break-up”, điểm khác nhau là tốc độ cháy tỉ lệ với nồng độ trung bình thay vì với nồng độ tức thời.

Trong ngọn lửa rối khuếch tán, tốc độ phản ứng hóa học rất lớn so với tốc độ hòa trộn, vì vậy tốc độ cháy có thể được xác định bởi tốc độ hòa trộn giữa nhiên liệu và oxygen trên kích cỡ phần tử, nghĩa là dựa vào tốc độ tiêu tán của các mặt tiếp giáp. Vì vậy, theo Mannussen tốc độ cháy của nhiên liệu được cho bởi:

R A.c . 

f f k

(2.29)



+ Trong đó: A là một hằng số, c f là nồng độ trung bình của nhiên liệu.

Trong vùng mà nồng độ oxygen thấp, tốc độ cháy được quyết định bởi nồng độ oxygen. Mặt khác, phản ứng xảy ra trong vùng mà nhiệt độ đủ lớn được giả định tỉ lệ với nồng độ sản vật cháy. Vì vậy, một cách tổng quát, tốc độ cháy được cho bởi công thức sau:



co cpro Rf A. .min c f ,2 ,B. k rf 1rf 





(2.30)

Sự dao động nồng độ không được kể đến một cách trực tiếp trong mô hình Magnussen.

Xấp xỉ đại lượng bảo toàn là mô hình cháy dùng nhiều nhất hiện nay trong việc đồng dạng ngọn lửa rối khuếch tán. Trong mô hình này, người ta giả sử tất cả các phần tử có cùng một hệ số khuếch tán. Giả thiết về động học phản ứng nhanh được sử dụng, vì trong phần lớn các trường hợp, tốc độ phản ứng rất cao so với tốc độ hòa trộn hỗn hợp. Từ đó, trạng thái nhiệt hóa học của hỗn hợp chẳng hạn như nồng độ các chất, khối lượng riêng, nhiệt độ có thể được xác định qua trung gian của đại lượng bảo toàn mà phương trình mô tả nó không chứa đại lượng sản sinh. Thành phần hỗn hợp f thường được chọn là đại lượng bảo toàn.

2.2.2. Mô hình cháy không đồng nhất thông qua đại lượng bảo toàn

2.2.2.1. Thành phần hỗn hợp

Trong quá trình cháy không đồng nhất, nhiên liệu và oxygen hòa trộn với nhau đến từ hai nguồn khác nhau, thành phần hỗn hợp định nghĩa bởi:

f M1

M1 M0

(2.31)

+ Trong đó: M1 và M0 là khối lượng của các thành phần trong hỗn hợp xuất phát từ nguồn nhiên liệu (1) và oxygen (0).

Theo định nghĩa này, tỉ lệ hỗn hợp được bảo toàn tuyệt đối, nghĩa là nó không sinh ra cũng như không mất đi trong quá trình cháy.

Định nghĩa thành phần hỗn hợp có thể được hiểu trong mối tương quan với

F rO 1r P

(2.32)

những phép đo chung trong hệ thống phản ứng. Hãy xét một hệ thống cháy đơn giản gồm một dòng nhiên liệu (F), một dòng chất oxy hóa (O), và dòng sản phẩm (P) được biểu diễn ở điều kiện phản ứng hoàn toàn như sau:

Trong đó r là tỉ lệ khối lượng không khí/nhiên liệu. Gọi hệ số tương đương là

 trong đó.

fuel /air Thucte

fuel /air 

Lythuyet

(2.33)

F rO r P

(2.34)

Phản ứng trong phương trình 2.31, dưới những điều kiện tổng quát hơn, có thể được viết như sau:

Nhìn vào vế trái của phương trình này, thành phần hỗn hợp cho toàn bộ hệ thống có thể rút gọn thành:

f 

r

(2.35)

Phương trình 2.35 cho phép tính thành phần hỗn hợp ở điều kiện phản ứng hoàn toàn =1 hay ở điều kiện hỗn hợp giàu >1 hay điều kiện hỗn hợp nghèo <1.

Trong quá trình cháy rối, vì nồng độ nhiêu liệu và oxygen là những đại lượng ngẫu nhiên và không liên tục, f cũng là một đại lượng ngẫu nhiên. Vì vậy cần phải tính đến sự dao động của nó. Phương pháp đơn giản là đưa vào khái niệm hàm mật độ xác suất đối với f. Hàm mật độ xác suất được xác định nhờ giá trị trung bình và độ lệch bình phương của f, mà hai đại lượng này là nghiệm số của hai phương trình chuyển sau đây [46]:

 ~ f  ~ f 1 f 

~ ~ ~

.U .V r t 

x r r r f r 



(2.36)

~ ~ ~ ~ 2

 ~ f ''2  ~ f ''2 1 f ''2 f c f ''2 ~

.U .V rtc f ''2

x r r r r f ''1 t x c

f '' D

(2.37)

Giá trị tức thời của nồng độ các chất, của nhiệt độ và khối lượng riêng được

xác định dựa vào giá trị tức thời của thành phần hỗn hợp f. Nếu biến phụ thuộc được gọi là ϕ(f) thì số trung bình kiểu Favre (density-weighted) và số trung bình kiểu Reynolds (unweighted) được xác định bởi hai biểu thức (2.37) và (2.38) sau đây:

~ 1

f .P f df

(2.38)

~ 1 f 

f .P f df

(2.39)

Và độ lệch bình phương của ϕ(f) cho bởi:

~ 0 2

''2 f .P f df 2

(2.40)

2.2.2.2. Hàm mật độ xác suất (fdp)

Một vấn đề cơ bản của mô hình cháy thông qua đại lượng bảo toàn là việc chọn hàm mật độ xác suất. Có nhiều dạng hàm số này được đề nghị:

- Hàm phân bố kiểu Gauss: Hawthorne và các đồng sự [52] trong công trình nghiên cứu cổ điển ngọn lửa rối khuếch tán đã đề nghị kiểu phân bố Gauss đối với sự dao động nồng độ. Dạng phân bố này được Lockwood và các đồng sự sử dụng trong việc đồng dạng hóa quá trình cháy bằng xấp xỉ đại lượng bảo toàn [46]. Hàm xác suất này được xác định trong khoảng 0 đến 1 có thể kèm theo hai phân bố Dirac ở hai đầu. Hàm được biểu diễn một cách tổng quát như sau:

1  1 f 2 

P f 2exp 2 .f , 0,1A.f B.f 1



(2.41)

Trong đó, hàm θ(f,γ1, γ2) được xác định bởi:

θ(𝑓, 𝛾 , 𝛾 ) = { 1 𝑛ế𝑢 𝛾1 ≤ 𝑓 ≤ 𝛾2

1 2 0 𝑛ế𝑢 𝑓 < 𝛾1 ℎ𝑎𝑦 𝑓 > 𝛾2

(2.42)

A và B là hai hằng số được định nghĩa bởi:

0 1  1 f 2 

A 2exp 2 df



(2.43)

1  1 f 2 

B 2exp 2 df

1 

(2.44)

- Hàm phân bố Beta: Hàm Beta được sử dụng rộng rãi trong nhiều công trình nghiên cứu [53], [54], [55], [56], [57]. Dạng tổng quát của phương trình như sau:

f1.1f 1

P f 1

fa1.af 1 df

(2.45)

Pf A0.f f ,0,1.f A1.1f 

(2.46)

- Hàm đa thức: Hàm này do Tamanini [58], [59] đề nghị và được Vachon cùng đồng sự sử dụng [60]. Một cách tổng quát, hàm được biểu diễn dưới dạng sau:

δ(f) là phân bố Dirac.

П(f) là hàm đa thức, định nghĩa bởi:

f f , f a, f a. n 11f fa 

a a 2.a a 



(2.47)

+ Trong đó: n là một số nguyên tương ứng với bậc của đa thức:

A0 f .df

fa a

(2.48)

fa a

A1 f .df

(2.49)

Hàm θ(f) được định nghĩa bởi (2.41).

2.2.2.3. Hàm của biến phụ thuộc ϕ(f)

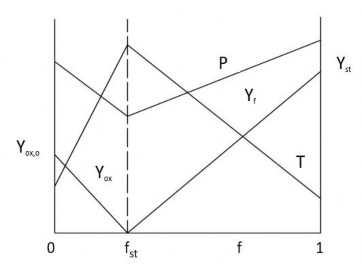
Hình (2.1) giới thiệu sự thay đổi của các đại lượng theo tỉ lệ hỗn hợp [61]. Hàm ϕ(f) đối với nồng độ, nhiệt độ và khối lượng riêng trong thực tế là phi tuyến. Để đơn giản việc tính toán, chúng ta chọn dạng tuyến tính như trong các công trình [60], [59], [46], [62].

Các hàm này được cho bởi:

𝑌𝑜𝑥,𝑜

𝑌𝑜𝑥 = − 𝑓 𝑓 + 𝑌𝑜𝑥,𝑜 𝑣ớ𝑖 𝑓 ≤ 𝑓𝑠𝑡

𝑠𝑡

(2.50)

𝑓 − 𝑓𝑠𝑡

𝑌𝑓 = 1 − 𝑓 𝑣ớ𝑖 𝑓 ≥ 𝑓𝑠𝑡

𝑠𝑡

(2.51)

h* c .T 1.Q Y

p f f

(2.52)

Đối với nhiệt độ, do sự xuất hiện của tổn thất bức xạ nên việc thiết lập mối quan hệ giữa nhiệt độ và đại lượng bảo toàn không thực hiện được. Hai giải pháp về vấn đề này dựa trên cùng một nguyên tắc: Tamanini [58] cho rằng tổn thất bức xạ tỉ lệ với năng lượng tỏa ra do quá trình cháy. Enthalpy toàn phần được viết như sau:

h*h*h*. f h*

1 0 0

(2.53)

Đại lượng q’ray mất đi nếu ra thay h bằng h* trong phương trình (2.52) và phương trình bảo toàn enthalpy được viết cùng dạng với đại lượng bảo toàn. Quan hệ giữa enthalpy và đại lượng bảo toàn có thể được thiết lập:

Crawford [63] đề nghị công thức để tính nhiệt độ thực tế của khí theo nhiệt độ đoạn nhiệt. Công thức này được dùng lại [60], [55]:

T ( f ) 4T ( f ) T ( f ).1 ad ad T 

ad ,max 

(2.54)

Hình 2.1: Quan hệ giữa nồng độ, nhiệt độ và khối lượng riêng theo tỉ hệ hỗn hợp‌

2.3. Mô hình cháy hỗn hợp đồng nhất

2.3.1. Thiết lập hệ phương trình cháy