Một số mô hình đo lường rủi ro trên thị trường chứng khoán Việt Nam - 24

Phụ lục 6. Kết quả ước lượng mô hình GARCH

Variable

Variable

CoefficientProb. Variable Coefficient

Variance Equation

Variance Equation

0

0

0

RBVH

RCTG

RDIG

Coefficient

Prob.

Prob.

C

-0.00025

0.8031

C

-0.00141

0.0246

C

-0.0025

0.0151

AR(1)

0.142602

0.0000

AR(3)

-0.5725

0.0000

AR(1)

0.154938

0.0007

MA(3)

0.531944

0.0000

Variance Equation

C

0.000151

0.0041

C

4.00E-05

0.0000

C

0.000225

0.000

RESID(-1)^2

0.222133

0.0007

RESID(-1)^2

0.226619

0.0000

RESID(-1)^2

0.461653

0.000

GARCH(-1)

0.601012

0.0000

GARCH(-1)

0.733516

0.0000

GARCH(-1)

0.433396

0.000

RDPM

REIB			RHPG
Variable	Coefficient	Prob.	Variable	Coefficient	Prob.	Variable	Coefficient	Prob.
C	-0.00063	0.3334	C	-0.00057	0.3663	C	-0.00216	0.0325
AR(1)	0.085453	0.0036				AR(1)	0.125774	0.0001
Variance Equation			Variance Equation			Variance Equation
C	5.40E-05	0.0000	C	0.000115	0.0000	C	0.000725	0.0000
RESID(-1)^2	0.212044	0.0000	RESID(-1)^2	0.240006	0.0000	RESID(-1)^2	0.177117	0.0000
GARCH(-1)	0.702183	0.0000	GARCH(-1)	0.44471	0.0000

Có thể bạn quan tâm!

• Kết Quả Hồi Quy Hàm Đồng Vượt Ngưỡng Theo Bg Và Biến Trễ
• Lược Đồ Tương Quan Của Các Chuỗi Lợi Suất
• Kết Quả Ước Lượng Hình Garch-Copula Động Của Các Chuỗi Lợi Suất Với Rvnindex
• Một số mô hình đo lường rủi ro trên thị trường chứng khoán Việt Nam - 25

Xem toàn bộ 209 trang tài liệu này.

RHSG

RIJC			RMBB
Variable	Coefficient	Prob.	Variable	Coefficient	Prob.	Variable	Coefficient	Prob.
C	-0.00116	0.3807	C	-0.00275	0.0191	C	-0.00108	0.2284
AR(1)	0.215811	0.0000	AR(1)	0.09949	0.0439
AR(4)	0.085371	0.0058
Variance Equation			Variance Equation			Variance Equation
C	0.000109	0.0672	C	0.000136	0.0066	C	3.70E-05	0.0213
RESID(-1)^2	0.104982	0.0089	RESID(-1)^2	0.355621	0.0000	RESID(-1)^2	0.223905	0.0048
GARCH(-1)	0.772676	0.0000	GARCH(-1)	0.59809	0.0000	GARCH(-1)	0.711445	0.0000

RMSN

ROGC			RPVF
Variable	Coefficient	Prob.	Variable	Coefficient	Prob.	Variable	Coefficient	Prob.
C	0.000885	0.3483	C	-0.00205	0.117	C	-0.00111	0.3176
AR(1)	0.174102	0.0000	AR(1)	0.125966	0.0016	AR(1)	0.156312	0.0000
						AR(7)	0.070918	0.0242
Variance Equation			Variance Equation			Variance Equation
C	6.35E-05	0.0027	C	5.71E-05	0.1968	C	6.55E-05	0.0917
RESID(-1)^2	0.164602	0.0002	RESID(-1)^2	0.105937	0.0441	RESID(-1)^2	0.118272	0.0068
GARCH(-1)	0.726453	0.0000	GARCH(-1)	0.834101	0.0000	GARCH(-1)	0.812692	0.0000

RSBT

RVCB			RCII
Variable	Coefficient	Prob.	Variable	Coefficient	Prob.	Variable	Coefficient	Prob.
C	-0.00036	0.6801	C	-0.00145	0.0159	C	-0.00074	0.284
AR(1)	0.153983	0.0000	AR(1)	0.033536	0.3723	AR(1)	0.141344	0.0000
AR(4)	0.052831	0.0714	MA(3)	-0.1169	0.0011
Variance Equation			Variance Equation			Variance Equation
C	6.85E-05	0.0006	C	0.000154	0.0000	C	3.09E-05	0.0002
RESID(-1)^2	0.14586	0.0000	RESID(-1)^2	0.299202	0.0000	RESID(-1)^2	0.227538	0.0000
GARCH(-1)	0.76254	0.0000	GARCH(-1)	0.396695	0.0000	GARCH(-1)	0.758045	0.0000

RFPT

RGMD			RKDC
Variable	Coefficient	Prob.	Variable	Coefficient	Prob.	Variable	Coefficient	Prob.
C	-0.0002	0.8004	C	-0.00214	0.0033	C	-0.00141	0.0355
AR(1)	0.065206	0.0000	AR(1)	0.185913	0.0000	AR(1)	0.163562	0.0000
Variance Equation			Variance Equation			Variance Equation
C	0.000126	0.0000	C	4.49E-05	0.0000
RESID(-1)^2	0.334762	0.0000	RESID(-1)^2	0.24789	0.0000	RESID(-1)^2	0.014368	0.0000
GARCH(-1)	0.603916	0.0000	GARCH(-1)	0.715999	0.0000	GARCH(-1)	0.985632	0.0000

RITA

RHNX			RVNINDEX
Variable	Coefficient	Prob.	Variable	Coefficient	Prob.	Variable	Coefficient	Prob.
C	-0.00156	0.0372	C	-0.00054	0.3195	C	-0.00038	0.427
AR(1)	0.121313	0.0000	AR(1)	0.145726	0.0000	AR(1)	0.246159	0.0000
Variance Equation			Variance Equation			Variance Equation
C	5.61E-05	0.0002	C	2.86E-05	0.0000	C	1.11E-05	0.0006
RESID(-1)^2	0.239319	0.0000	RESID(-1)^2	0.220188	0.0000	RESID(-1)^2	0.175032	0.0000
GARCH(-1)	0.728945	0.0000	GARCH(-1)	0.738369	0.0000	GARCH(-1)	0.788232	0.0000

Phụ lục 7. Kết quả ước lượng mô hình CCC

Các phương trình trung bình:

RCII = -0.00125401047294+0.0839002961242*RCII(-1) +e RFPT = -0.00160353921984+0.0605581155104*RFPT(-1)+e RGMD = -0.00253729651678+0.0860966474515*RGMD(-1)+e RKDC = -0.00101797052893+0.10143705969*RKDC(-1)+e RITA = -0.00207396143231+0.078632313595*RITA(-1)+e

RVNINDEX=-0.000735170643729+0.119094618122*RVNINDEX(-1)+e

Các phương trình phương sai:

GARCH1 = 0.000105455532449 + 0.278904449294*RESID1(-1)^2 + 0.664381961928*GARCH1(-1) Prob. (0.000) (0.000) (0.000)

GARCH2 = 9.2133004015e-05 + 0.325559387907*RESID2(-1)^2 + 0.576824849594*GARCH2(-1) Prob. (0.000) (0.000) (0.000)

GARCH3 = 8.41890841123e-05 + 0.292234766559*RESID3(-1)^2 + 0.672738965563*GARCH3(-1) Prob. (0.000) (0.000) (0.000)

GARCH4 = 6.4231402351e-05 + 0.265810362863*RESID4(-1)^2 + 0.691411014647*GARCH4(-1) Prob. (0.000) (0.000) (0.000)

GARCH5 = 0.000132476015096 + 0.253438220487*RESID5(-1)^2 + 0.667809573438*GARCH5(-1) Prob. (0.000) (0.000) (0.000)

GARCH6 = 3.73793471141e-05 + 0.174654311498*RESID6(-1)^2 + 0.748735668436*GARCH6(-1)

Prob. (0.000) (0.000) (0.000)

Các phương trình hiệp phương sai:

COV1_2 = 0.498282334165*SQRT(GARCH1*GARCH2) Prob. (0.000)

COV1_3 = 0.526742671525*SQRT(GARCH1*GARCH3) Prob. (0.000)

COV1_4 = 0.445011987939*SQRT(GARCH1*GARCH4) Prob. (0.000)

COV1_5 = 0.51451364586*SQRT(GARCH1*GARCH5) Prob. (0.000)

COV1_6 = 0.660144651063*SQRT(GARCH1*GARCH6) Prob. (0.000)

COV2_3 = 0.554149302091*SQRT(GARCH2*GARCH3) Prob. (0.000)

COV2_4 = 0.4600654794*SQRT(GARCH2*GARCH4) Prob. (0.000)

COV2_5 = 0.497339740627*SQRT(GARCH2*GARCH5) Prob. (0.000)

COV2_6 = 0.725294839971*SQRT(GARCH2*GARCH6) Prob. (0.000)

COV3_4 = 0.472885962835*SQRT(GARCH3*GARCH4) Prob. (0.000)

COV3_5 = 0.591013694372*SQRT(GARCH3*GARCH5) Prob. (0.000)

COV3_6 = 0.727263011566*SQRT(GARCH3*GARCH6) Prob. (0.000)

COV4_5 = 0.45871954421*SQRT(GARCH4*GARCH5) Prob. (0.000)

COV4_6 = 0.614401341392*SQRT(GARCH4*GARCH6) Prob. (0.000)

COV5_6 = 0.705111683562*SQRT(GARCH5*GARCH6) Prob. (0.000)

Phụ lục 8. Đồ thị các chuỗi phương sai có điều kiện

.0020

.0016

.0012

.0008

.0004

.0000

garchrvnindex

250 500 750 1000 1250

.005

.004

.003

.002

.001

.000

garchrhnx

250 500 750 1000 1250

.05

.04

.03

.02

.01

.00

garchrita

250 500 750 1000 1250

Conditional variance

Conditional variance

Conditional variance

.035

.030

.025

.020

.015

.010

.005

garchrcii

.05

.04

.03

.02

.01

garchrfpt

.016

.014

.012

.010

.008

.006

.004

.002

garchrgmd

.000

.0024

.0020

.0016

.0012

.0008

.0004

.0000

.06

.05

.04

.03

250 500 750 1000 1250

Conditional variance

garchrkdc

250 500 750 1000 1250

Conditional variance

garchrdig

.00

.0018

.0016

.0014

.0012

.0010

.0008

.0006

.0004

.0002

.0024

.0020

.0016

.0012

250 500 750 1000 1250

Conditional variance

garchrbvh

100 200 300 400 500 600 700 800

Conditional variance

garchrdpm

.000

.008

.007

.006

.005

.004

.012

.010

.008

.006

.004

.002

.000

250 500 750 1000 1250

Conditional variance

garchrctg

100 200 300 400 500 600 700 800

Conditional variance

garchreib

.02

.01

.00

100 200 300 400 500 600 700 800

.0008

.0004

.0000

250 500 750 1000 1250

.003

.002

.001

.000

100 200 300 400 500 600 700

Conditional variance

Conditional variance

Conditional variance

.024

.020

.016

.012

.008

.004

.000

garchrhpg

250 500 750 1000 1250

.006

.005

.004

.003

.002

.001

.000

garchrhsg

250 500 750 1000

.006

.005

.004

.003

.002

.001

.000

garchrhsg

250 500 750 1000

Conditional variance

Conditional variance

Conditional variance

.0024

garchrmbb

.0020

garchrmsn

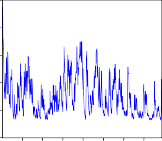
.0035

garchrogc

.0020

.0016

.0012

.0008

.0004

.0016

.0012

.0008

.0004

.0030

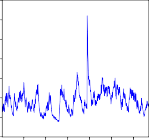
.0025

.0020

.0015

.0010

.0005

.0000

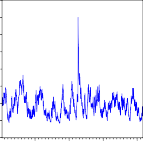
.0040

.0035

.0030

.0025

.0020

.0015

.0010

.0005

50 100 150 200 250

Conditional variance

garchrpvf

.0000

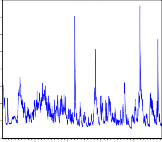
.0040

.0035

.0030

.0025

.0020

.0015

.0010

.0005

100 200 300 400 500 600 700

Conditional variance

garchrsbt

.0000

.007

.006

.005

.004

.003

.002

.001

100 200 300 400 500 600

Conditional variance

garchrvcb

.0000

250 500 750 1000

.0000

250 500 750 1000

.000

100 200 300 400 500 600 700 800

Conditional variance

Conditional variance

Conditional variance

Phụ lục 9. Một số chương trình Matlab

% Ước lượng VaR và ES bằng mô hình GARCH-EVT-copula. load('data')

T = size(data,1); nIndices = size(data,2); for i=1:nIndices

spec(i) = garchset('Distribution' , 'T' , 'Display', 'off', ...

'VarianceModel', 'GARCH', 'P', 1, 'Q', 1, 'R',0)

end

residuals = NaN(T, nIndices); % preallocate storage sigmas = NaN(T, nIndices);

for i = 1:nIndices

[spec(i) , errors, LLF, ...

residuals(:,i), sigmas(:,i)] = garchfit(spec(i), data(:,i)); end

residuals = residuals ./ sigmas;

nPoints = 200; % # of sampled points of kernel-smoothed CDF tailFraction = 0.1; % Decimal fraction of residuals allocated to each tail OBJ = cell(nIndices,1); % Cell array of Pareto tail objects

for i = 1:nIndices

OBJ{i} = paretotails(residuals(:,i), tailFraction, 1 - tailFraction, 'kernel'); end

U = zeros(size(residuals)); for i = 1:nIndices

U(:,i) = OBJ{i}.cdf(residuals(:,i)); % transform margin to uniform end

%[R, DoF] = copulafit('t', U, 'Method', 'ApproximateML'); % fit the copula RHOHAT = copulafit('Gaussian',U);%fit the copula-Gaussian

s = RandStream.getDefaultStream(); reset(s)

nTrials = 5000; % # of independent random trials horizon = 1; % VaR forecast horizon

Z = zeros(horizon, nTrials, nIndices); % standardized residuals array

%U = copularnd('t', R, DoF, horizon * nTrials); % t copula simulation

U = copularnd('Gaussian', RHOHAT, horizon * nTrials);% Gaussian copula

%simulation

for j = 1:nIndices

Z(:,:,j) = reshape(OBJ{j}.icdf(U(:,j)), horizon, nTrials); end

preResidual = residuals(end,:) .* sigmas(end,:); % presample model residuals preSigma = sigmas(end,:); % presample volatilities

preReturn = data(end,:); % presample returns simulatedReturns = zeros(horizon, nTrials, nIndices);

for i = 1:nIndices