Mối Quan Hệ Giữa Tần Số Gen Và Các Phương Sai Thành Phần

quần thể nên phương sai chỉ là trung bình của bình phương các giá trị này. Cách tính toán cụ thể như sau:

6.2. Tính toán các phương sai thành phần

Tính phương sai cộng gộp (phương sai giá trị giống):

Kiểu gen Tần số Giá trị cộng gộp (giá trị giống) Tần số x (Giá trị giống)2

2 2 2 2

A1A1 p 2q4p q 

2 2

A1A2 2pq (q-p)2pq(q-p) 

2 2 2 2

A2A2 q -2p4p q 

2 2 2 2 2 2 2 2

Céng: 4p2q22 + 2pq(q-p)22 + 4p2q22 VA = 4p q + 2pq(q-p) + 4p q 

= 2pq22(2pq + q2 - 2pq + p2 +2pq)

= 2pq22(p2 + 2pq + q2)

= 2pq22(p+q)2

= 2pq22 [2.12]

Thay giá trị của theo biểu thức [2.7]:

2 2

VA = 2pq [a + d(q-p)] [2.13]

Tính phương sai sai lệch trội:

Kiểu gen Tần số Sai lệch trội Tần số x (Sai lệch trội)2

2 2 2 4 2

A1A1 p -2q d 4p q d

3 3 2

A1A2 2pq 2pqd 8p q d

2 2 4 2 2

A2A2 q -2p d 4p q d

Céng: 4p2q4d2 + 8p3q3d2 + 4p4q2d2 VD = 4p2q4d2 + 8p3q3d3 + 4p4q2d2

= 4p2q2d2(q2 + 2pq + p2)

VD = (2pqd)2 [2.14]

Tính phương sai di truyền:

VG = VA + VD + 2CovAD

trong đó: CovAD là hiệp phương sai giữa giá trị giống và sai lệch trội, cũng do các giá trị đã được tính theo chênh lệch so với trung bình quần thể nên hiệp phương sai chỉ là trung bình của bình phương các giá trị này. Cách tính toán cụ thể như sau:

CovAD = Tần số x Giá trị giống x Sai lệch trội

2

2q	-2q2d		p2(2q)(-2q2d)
(q-p)	2pqd		2pq(q-p)(2pqd)
-2p	-2p2d		q2(-2p)(-2p2d)

Có thể bạn quan tâm!

• Di truyền số lượng và chọn giống vật nuôi - 1
• Di truyền số lượng và chọn giống vật nuôi - 2
• Di truyền số lượng và chọn giống vật nuôi - 3
• Tính Hệ Số Cận Huyết Căn Cứ Vào Quy Mô Và Cấu Trúc Quần Thể
• Quan Hệ Di Truyền Và Hiệp Phương Sai Di Truyền Giữa Một Số Họ Hàng Thân Thuộc
• Một Số Ước Tính Hệ Số Di Truyền Của Các Tính Trạng Năng Suất Động Vật (Theo Taylor, Bogart, 1988)

Xem toàn bộ 128 trang tài liệu này.

Kiểu gen Tần số Giá trị giống Sai lệch trội Tần số x GT giống xSai lệch trội A1A1 p

A1A2 2pq

2

A2A2 q

Céng: -4p2q3d+ 4p2q3d- 4p3q2d+ 4p3q2d= 0 Do CovAD = 0 nên: VG = VA + VD

Thay các giá trị của VA và VD trong các biểu thức [2.13] và [2.14], ta có:

2 2 2

VG = 2pq [a + d(q-p)] + (2pqd) [2.15]

Ví dụ: Dòng chuột có gen lùn pg, với tần số q=0,1 ; a=4 và d=2

2 2

VA = 2 x 0,9 x 0,1 [4 + 2 (0,1 - 0,9)] = 0,18 x (2,4) = 1,0368

2 2

VD = (2 x 0,9 x 0,1 x 2) = (0,36) = 0,1296 VG = VA + VD = 1,0368 + 0,1296 = 1,1664

Nếu tần số q=0,4, thì:

2 2

VA = 2 x 0,4 x 0,6 [4 + 2 (0,4 - 0,6)] = 0,48 x (3,6) = 6,2208

2 2

VD = (2 x 0,4 x 0,6 x 2) = (0,96) = 0,9216

VG = VA + VD = 6,2208 + 0,9216 = 7,1424

Tóm lại: q = 0,1 q = 0,4

Phương sai giá trị giống

VA	1,0368	6,2208
Phương sai sai lệch trội	VD	0,1296	0,9216
Phương sai giá trị kiểu gen	VG	1,1164	7,1424

Như vậy, phương sai giá trị giống chiếm tỷ trọng lớn nhất trong tổng số phương sai kiểu gen:

Nếu q=0,1; VA (%) chiếm 1,0368/1,1164 = 88,89% Nếu q=0,4; VA (%) chiếm 6,2208/7,1424 = 87,10%

Nhận xét nêu trên sẽ được ứng dụng trong việc ước tính các tham số di truyền.

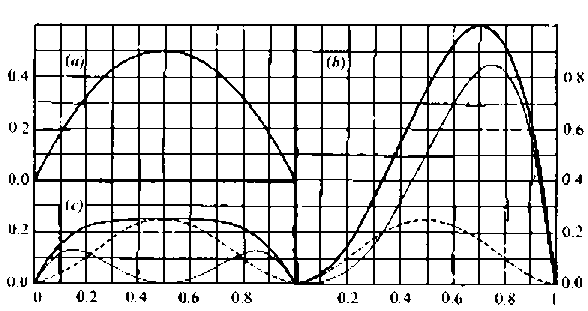
Mối quan hệ giữa tần số gen và các phương sai thành phần được mô tả trên hình 2.1.

Tần số gen, q

Hình 2.1. Mối quan hệ giữa tần số gen và các phương sai thành phần

Ghi chú: Đường đậm nét là phương sai kiểu gen, đường mảnh hơn là phương sai cộng gộp, đường không liền nét là phương sai sai lệch trội. Tần số gen q tương ứng với allen lặn. (a) Không trội, nghĩa là d=0. (b) Trội hoàn toàn, nghĩa là d=a. (c) Siêu trội thuần, nghĩa là a=0.

Trên thực tế, để có thể ước tính được các phương sai thành phần người ta sử dụng các phương pháp sau:

- Theo dõi, phân tích sự giống nhau giữa các cá thể có quan hệ họ hàng sẽ ước tính

được 2 loại phương sai thành phần: VA : (VD + VI + VE)

- Theo dõi, phân tích sự giống nhau giữa các dòng cận huyết sẽ ước tính được 2 loại phương sai thành phần: VG : VE

- Phối hợp cả 2 phương pháp trên sẽ ước tính được 3 loại phương sai thành phần: VA : (VD + VI) : VE

Các ứng dụng ước tính phương sai thành phần sẽ được trình bầy trong phần ước tính

các tham số di truyền.

Chương 3

Quan hệ di truyền giữa các cá thể

Chỉ có dựa vào việc theo dõi hệ phổ vật nuôi người ta mới có thể xác định được mối quan hệ di truyền giữa các cá thể, đánh giá được mức độ cận huyết của một cá thể, trên cơ sở

đó ngăn ngừa các khả năng giao phối cận huyết có thể xảy ra. Hiểu biết đầy đủ về mối quan hệ di truyền giữa một số con vật họ hàng giúp chúng ta nắm vững được bản chất của các phương pháp xác định các tham số di truyền được đề cập tới trong chương tiếp theo.

1. HƯ phỉ

Hệ phổ, còn gọi là hệ phả (Pedigree) là sơ đồ về nguồn gốc huyết thống của con vật.

Để ghi chép hệ phổ, người ta có thể sử dụng một vài phương pháp khác nhau, do đó hình thành một số loại hệ phổ khác nhau:

- Hệ phổ dọc: Được ghi theo nguyên tắc mỗi hàng là một thế hệ, thế hệ trước ghi ở hàng dưới, thế hệ sau ghi ở hàng trên; trong cùng một hàng, con đực được ghi ở bên phải, con cái được ghi ở bên trái.

Ví dụ: Hệ phổ của cá thể X có thế hệ trước của X là bố mẹ (thế hệ I) có bố (B), mẹ (M). Thế hệ trước bố mẹ là ông bà (thế hệ II) có bố của bố tức ông nội (BB), mẹ của bố tức bà nội (MB), bố của mẹ tức ông ngoại (BM), mẹ của mẹ tức bà ngoại (MM). Thế hệ trước ông bà (cụ, thế hệ III) cũng theo nguyên tắc như vậy. Sơ đồ như sau:

M				B
MM		BM		MB		BB
MMM	BMM	MBM	BBM	MMB	BMB	MBB	BBB

X

I II III

- Hệ phổ ngang: Được ghi theo nguyên tắc mỗi cột là một thế hệ, thế hệ trước ghi ở cột bên phải, thế hệ sau sau ghi ở cột bên trái; trong cùng một cột, con đực ghi ở hàng trên, con cái ghi ở hàng dưới.

Ví dụ: Cũng hệ phổ của cá thể X và các ký hiệu các cá thể có quan hệ họ hàng như trên, sơ đồ như sau:

I II III

BBB

BB

MBB

B

BMB

MB

MMB

X

BBM

BM

MBM

M

BMM

MM

MMM

Tại các vị trí của các con vật có họ hàng trong hệ phổ, người ta ghi lại số hiệu hoặc tên của con vật. Mỗi cá thể được đánh số theo các phương pháp quy định như: cắt số tai (đối với

lợn), xăm số vào tai hoặc đeo biển nhựa (trên đó có ghi số) vào tai (đối với lợn hoặc bò), đeo biển nhôm (trên đó có ghi số) ở gốc cánh hoặc ở chân (đối với gia cầm) ...

- Trong thực tế, hệ phổ thường được ghi theo kiểu hệ phổ ngang, nhưng không hoàn toàn tuân thủ theo các nguyên tắc ghi của hệ phổ này. Ví dụ:

1

1 2 3 4

2

S

S D

X

1 X

D

3

Có thể có 3 dạng hệ phổ sau:

+ Hệ phổ đầy đủ: Ghi chép toàn bộ các con vật ở các thế hệ khác nhau

+ Hệ phổ tóm tắt: Chỉ ghi chép lại những con vật có liên quan huyết thống trực tiếp với một tổ tiên nhất định

+ Hệ phổ thu gọn: Tương tự như hệ phổ tóm tắt, nhưng mỗi con vật chỉ xuất hiện 1 lần duy nhất trong hệ phổ.

Ví dụ về 3 dạng hệ phổ:

S

1

S S 1 X S S 2

X X D S X 1

1

D D 2 1 D

2

2

2. Quan hƯ di truyỊn

Để mô tả mối quan hệ di truyền giữa 2 cá thể nhưng chỉ xem xét về tác động cộng gộp của các gen, người ta sử dụng khái niệm hệ số thân thuộc và quan hệ di truyền cộng gộp.

2.1. Hệ số thân thuộc

Khái niệm này do Malécôt (1948) đề xuất. Hệ số thân thuộc giữa 2 cá thể là xác suất 1 gen rút ngẫu nhiên từ 1 locus bất kỳ của cá thể này là cùng nguồn gốc (cùng là bản sao chép hoá học từ 1 gen gốc, không do đột biến gây nên) với 1 gen rút ngẫu nhiên từ locus tương ứng của cá thể kia.

Giả sử, 2 cá thể X và Y tại một locus bất kỳ chúng có các gen tương ứng như sau: X Y

Ai Aj AÝ'Aj'

Từ locus của X rút ngẫu nhiên được gen Ai, còn từ Y rút ngẫu nhiên được gen Aj. Xác suất để 2 gen Ai và Aj cùng nguồn gốc (đều được sao chép từ 1 gen gốc, không phải do đột biến gây nên) được ký hiệu là: P(Ai=Aj).

Hệ số thân thuộc giữa X và Y, ký hiệu là fXY:

fXY = 1/4 [P(Ai=Ai') + P(Ai=Aj') + P(Aj=Ai') + P(Aj=Aj') ]

Nếu X và Y là 2 anh chị em ruột, bố mẹ chúng không cận huyết thì xác suất mỗi trường hợp đều là 1/4. Vậy:

fXY = 1/4 (1/4 + 1/4 + 1/4 + 1/4) = 1/4

Hệ số thân thuộc của chính bản thân con vật sẽ được tính trên cơ sở hệ số thân thuộc của X với chính X:

X X

Ai Aj AÝAj

fXY = 1/4 [P(Ai=Ai) + P(Ai=Aj) + P(Aj=Aj) + P(Aj=Ai) ] fXY = 1/4 (1 + 0 + 1 + 0) = 1/2

2.2. Quan hƯ di truyỊn céng gép

Quan hệ di truyền cộng gộp giữa hai cá thể là hai lần xác suất rút ngẫu nhiên 1 gen từ 1 locus của cá thể này là cùng nguồn gốc (cùng là bản sao chép hoá học từ 1 gen gốc, không do đột biến gây nên) với 1 gen rút ngẫu nhiên từ locus tương ứng của cá thể kia. Như vậy, quan hệ di truyền cộng gộp bằng hai lần hệ số thân thuộc, quan hệ di truyền cộng gộp giữa X và Y được ký hiệu là aXY:

aXY = 2 fXY

Có thể sử dụng phép tính xác suất để tính quan hệ di truyền cộng gộp của một số quan hệ họ hàng. Sau đây là một vài ví dụ:

- Tính quan hệ di truyền cộng gộp giữa bố (hoặc mẹ) với con:

Giả sử tại 1 locus bất kỳ, bố (X) và mẹ (Y) có các gen tương ứng là i,j và k,l. Do đó con có thể có các gen i, k hoặc i, l hoặc j, k hoặc j, l:

Bè - MÑ Xij YklCon Zik

il jk jl

Xác suất các gen rút ngẫu nhiên từ locus này của bố và của con như sau:

Gen rút ngẫu nhiên từ Z (xác suất mỗi sự kiện bằng 1/4)

	i	j	k	l
Gen rút ngẫu nhiên từ X	i	1/8	1/8	1/8	1/8
(xác suất mỗi sự kiện bằng 1/2)	j	1/8	1/8	1/8	1/8

do vậy:

Do đó:

Trong bảng trên, chỉ có 2 trường hợp các gen rút được là cùng nguồn gốc (i=i và j=j),

1/8 + 1/8

fXZ = = 1/4 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8 + 1/8

aXZ = 2 fXZ = 2 x 1/4 = 1/2

- Tính quan hệ di truyền cộng gộp giữa 2 anh chị em ruột (cùng bố cùng mẹ):

Giả sử tại 1 locus bất kỳ, bố (X) và mẹ (Y) có các gen tương ứng là i,j và k,l. Do đó hai anh chị em ruột Z và W đều có thể có các gen i, k hoặc i, l hoặc j, k hoặc j, l:

Bè - MÑ

Xij	Ykl
Anh chị em ruột	Zi k i l	Wi k i l
	j,k j l	j k j,l

Xác suất rút ngẫu nhiên các gen từ locus này của Z và W như sau:

Genotyp cđa Z

	i k	i l	j k	j l
i k	1/2	1/4	1/4	0
Genotyp	i l	1/4	1/2	0	1/4
cđa W	j k	1/4	0	1/2	1/4
	j l	0	1/4	1/4	1/2

Xác suất trung bình của các trường hợp trên là:

(4 x 1/2 + 4 x 0 + 8 x 1/4) : 16 = 1/4

Do đó : fZW = 1/4

aZW = 2 fZW = 2 x 1/4 = 1/2

Tương tự như vậy, có thể tính được quan hệ di truyền cộng gộp giữa một số quan hệ họ hàng như sau:

Quan hệ họ hàngQuan hệ di truyền cộng gộp(aXY) Bố hoặc mẹ – Con 1/2

Ông hoặc bà - Cháu 1/4

Đời trước - Đời sau (cách nhau n thế hệ) (1/2)n Anh chị em ruột 1/2

Anh chị em nửa ruột thịt 1/4

(cùng bố khác mẹ hoặc cùng mẹ khác bố)

2.3. Hệ số cận huyết

Hệ số cận huyết của một cá thể là xác suất mà 2 gen rút ngẫu nhiên tại một locus bất kỳ của cá thể đó cùng nguồn gốc với nhau (cùng là bản sao chép hoá học từ một gen gốc, không phải là giống nhau do đột biến).

Xét cá thể X, bố và mẹ của X là S và D, quan hệ di truyền cộng gộp giữa S và D là aSD. Hệ số cận huyết của cá thể X được ký hiệu là FX, do đó:

FX = 1/2 aSD

2.4. Cách tính toán quan hệ di truyền cộng gộp và hệ số cận huyết

Có thể sử dụng một trong 2 cách sau đây để tính toán quan hệ di truyền cộng gộp và hệ số cận huyết.

2.4.1. Sử dụng công thức (Wright, 1922)

Xét hệ phổ của cá thể V như sau:

W

Z

X Y

V

X và Y có tổ tiên chung là W.

Rút ngẫu nhiên 1 gen từ X, gọi gen này là i Rút ngẫu nhiên 1 gen từ Y, gọi gen này là j

Theo định nghĩa quan hệ di truyền cộng gộp giữa X và Y, ta có:

aXY = 2 P(i=j)

Tổ tiên chung W truyền ngẫu nhiên 1 gen cho Z, truyền ngẫu nhiên 1 gen cho Y. Nếu W không cận huyết thì xác suất 2 gen này cùng nguồn gốc (giả sử đều là i) sẽ bằng 1/2. Nếu W cận huyết với hệ số cận huyết là FW thì xác suất này sẽ bằng 1/2 + FW/2 = (1 + FW)/2.

Cho rằng 2 gen này cùng nguồn gốc và đều là i, xác suất Z truyền gen i cho X bằng

1/2. Cho rằng X nhận được gen i, xác suất rút ngẫu nhiên được gen i từ X bằng 1/2, xác suất rút ngẫu nhiên được gen i từ Y cũng bằng 1/2.

Tất cả các sự kiện trên độc lập với nhau, do đó xác suất gen i và j cùng nguồn gốc như

sau:

Nếu:

P(i=j) = (1 + FW)/2 . 1/2 . 1/2 . 1/2

n là số thế hệ (số đường nối) từ tổ tiên chung W tới X (bố của V), xác suất W truyền gen i cho X sẽ là (1/2)n

p là số thế hệ (số đường nối) từ tổ tiên chung W tới Y (mẹ của V), xác suất W truyền gen i cho Y sẽ là (1/2)p

Do đó:

và:

P(i=j) = (1 + FW)/2 . (1/2) . (1/2)

W

n p

P(i=j) = (1/2)n+p(1 + F )/2

aXY = 2 P(i=j) = (1/2)n+p(1 + FW) FV = 1/2 aXY = (1/2)n+p(1 + FW)/2

= (1/2)n+p+1(1 + FW) hoỈc:

= 1/2 [(1/2)n+p(1 + FW)]

Nếu Z có nhiều tổ tiên chung, hoặc một tổ tiên chung có nhiều đường nối khác nhau

tới bố và mẹ của Z thì:

Quan hệ di truyền cộng gộp giữa X và Y được tính theo công thức:

n +p

aXY = (1/2) k k (1 + Fk) [3.1]

k

trong đó: nk, pk là số thế hệ (số đường nối) từ tổ tiên chung tới X và Y Fk là hệ số cận huyết của tổ tiên chung

Hệ số cận huyết của cá thể V được tính theo công thức: