Di truyền số lượng và chọn giống vật nuôi

Di truyền số lượng và chọn giống vật nuôi

DI TRUYỀN SỐ LƯỢNG VÀ CHỌN GIỐNG VẬT NUÔI

Phần lý thuyết

Chương 1

cấu trúc di truyền quần thể và định luật hardy-weinberg

Quần thể là một nhóm gồm các cá thể mà chúng có thể giao phối với nhau. Có thể hiểu quần thể bao gồm toàn bộ một giống, một loài, một đàn hoặc một bầy, thậm chí chỉ một nhóm con vật trong một đàn vật. Di truyền học quần thể là một ngành khoa học nghiên cứu các nhân tố ảnh hưởng tới tần số gen, tần số kiểu gen trong một quần thể. Trong chương này, khi xem xét cấu trúc di truyền của một quần thể cũng như định luật Hardy-Weinberg, chúng ta sẽ chủ yếu sử dụng mô hình hai allen tại một locus. Đây là mô hình đơn giản nhất để có thể dễ dàng nắm được các khái niệm cơ bản và các nguyên tắc chung.

1. Cấu trúc di truyền của quần thể

Cấu trúc di truyền của một quần thể được đặc trưng bởi:

- Các kiểu gen mà các cá thể trong quần thể đó có;

- Số lượng của mỗi kiểu gen đó.

Giả sử chỉ xét một locus riêng biệt trên một nhiễm sắc thể thường, có hai allen tại locus này là A1 và A2, như vậy sẽ có 3 kiểu gen là A1A1, A1A2 và A2A2. Số lượng mỗi kiểu gen thường được biểu thị bằng tỷ lệ hoặc phần trăm số cá thể thuộc kiểu gen đó. Tỷ lệ hoặc phần trăm của mỗi một kiểu gen trong quần thể được gọi là tần số kiểu gen. Tổng tần số của tất cả các kiểu gen trong quần thể luôn luôn bằng 1 hoặc 100%.

Ví dụ: Màu lông của bũ BBB (Blanc-Bleu-Belge) do các gen N và n quy định.

- Bò NN có lông màu trắng

- Bò Nn có lông màu xanh

- Bò nn có lông màu đen.

Trong khi đó màu lông của bũ Shorthorn do các gen R và r quy định.

- Bò RR có lông màu đỏ

- Bò Rr có lông lang trắng đỏ

- Bò rr có lông màu trắng.

Bảng 1.1. Tần số kiểu gen của quần thể bò BBB và Shorthorn (Hanset, 1983)

Loại	Kiểu gen
bò	NN hoỈc rr	Nn hoỈc Rr	nn hoỈc RR
Tần số	BBB	0,49	0,42	0,09
kiểu gen	Shorthorn	0,09	0,42	0,49

Có thể bạn quan tâm!

Xem toàn bộ 128 trang tài liệu này.

Cần lưu ý rằng, khi truyền đạt cho thế hệ sau, tần số kiểu gen của thế hệ bố mẹ sẽ bị thay đổi, các kiểu gen ở thế hệ con cái được thành lập trên cơ sở các gen mà thế hệ bố mẹ truyền cho hợp tử. Vì vậy nghiên cứu cấu trúc di truyền của một quần thể cần phải xem xét tới sự truyền đạt các gen từ thế hệ trước sang thế hệ sau và do đó ngoài khái niệm tần số kiểu gen, ta cần đề cập tới khái niệm tần số gen.

Tần số gen là tỷ lệ hoặc phần trăm của các loại allen có tại mỗi một locus. Tần số của tất cả các allen tại bất kỳ locus nào cũng luôn luôn bằng 1 hoặc 100%.

VÝ dô: Cã hai allen A1 và A2 tại một locus nào đó, số lượng mỗi kiểu gen của 100 cá thể như sau:

A1A1 A1A2 A2A2 Tỉng sè

Số cá thể

40	50	10		100
Sè gen A1	80	50	0		130
Sè gen A2	0	50	20		70

Như vậy, có 130 gen A1 và 70 gen A2, tần số A1 và A2 là 0,65 và 0,35. Mối quan hệ giữa tần số kiểu gen và tần số gen như sau:

	Gen				Kiểu gen
A1		A2		A1 A1	A1A2	A2 A2
Tần số	p		q		P	H	Q

Ta cã: p + q = 1

P + H + Q = 1

p = P + 1/2 H

q = Q + 1/2 H [1.1]

¸p dụng phương trình [1.1], từ các số liệu tần số kiểu gen của Hanset (1983), ta có thể tính được các tần số gen ở 2 quần thể bò như sau:

Tần số gen N ở bũ BBB là:

Tần số gen n ở bũ BBB là:

0,49 + 1/2 (0,42) = 0,70

0,09 + 1/2 (0,42) = 0,30

Tương tự như vậy, ta tính được các tần số gen ở bũ Shorthorn như sau: Tần số gen R ở bũ Shorthorn là:

0,49 + 1/2 (0,42) = 0,70

Tần số gen r ở bũ Shorthorn là:

0,09 + 1/2 (0,42) = 0,30

Kết quả được tập hợp trong bảng sau:

Loại	Kiểu gen			Gen
bò	NN hoỈc rr	Nn hoỈc Rr	nn hoỈc RR	N hoỈc R	n hoỈc r
Tần	BBB	0,49	0,42	0,09	0,70	0,30
sè	Shorthorn	0,09	0,42	0,49	0,70	0,30

Các đặc tính di truyền của một quần thể sẽ bị thay đổi trong quá trình truyền đạt gen từ thế hệ trước sang thế hệ sau. Các yếu tố tác động vào quá trình truyền đạt gen sẽ gây nên những biến đổi đặc tính di truyền quần thể. Các yếu tố này bao gồm:

- Kích thước quần thể: Các gen được truyền cho thế hệ sau chỉ là một số trong vô số các gen của thế hệ bố mẹ. Có thể xem đây là trường hợp lấy mẫu ngẫu nhiên. Vì vậy, có thể bỏ qua sai số do việc lấy mẫu này bằng cách giả thiết rằng ta chỉ nghiên cứu trên các quần thể có kích thước lớn. Trong thực tế, quần thể lớn là quần thể có hàng trăm cá thể trưởng thành.

- Tỷ lệ thụ thai và tỷ lệ sống: Các kiểu gen của thế hệ bố mẹ có thể có các tỷ lệ thụ thai khác nhau do đó sẽ không tạo được các loại hợp tử có số lượng như nhau. Các hợp tử cũng có tỷ lệ sống khác nhau, do đó tần số gen của thế hệ mới sẽ thay đổi trong quá trình chúng phát triển thành những cá thể trưởng thành để sinh ra thế hệ sau. Quá trình này được gọi là chọn lọc.

- Di trú và đột biến: Tần số gen của quần thể có thể thay đổi do sự di nhập những cá thể từ một quần thể khác hoặc do đột biến gen.

- Hệ thống giao phối: Kiểu gen đời con được xác định do sự kết hợp giữa 2 giao tử bố và mẹ, sự kết hợp này lại chịu sự ảnh hưởng của cặp kiểu gen giao phối ở đời bố mẹ. Nếu giao phối là ngẫu nhiên, nghĩa là các cá thể bất kỳ đều có cùng một cơ hội phối giống với bất cứ một cá thể khác, thì tần số kiểu gen và tần số gen của quần thể không thay đổi. Tuy nhiên, giao phối ngẫu nhiên sẽ dẫn tới khuynh hướng giao phối giữa những cá thể cùng họ hàng.

2. Định luật Hardy - Weinberg

2.1. Định luật Hardy - Weinberg

Hardy - Weinberg (1908) phát hiện ra định luật sau:

Trong một quần thể lớn, giao phối ngẫu nhiên, không có chọn lọc, đột biến hoặc di cư, tần số gen và tần số kiểu gen không thay đổi qua các thế hệ.

Nếu tần số hai allen ở bố mẹ là p và q thì tần số kiểu gen ở đời con là p2, 2pq và q2.

Gen ở bố mẹ Kiểu gen ở đời con A1 A2 A1A1 A1A2 A2A2

Tần số p q p2 2pq q2 [1.2]

Mối quan hệ giữa tần số gen và kiểu gen này chỉ áp dụng cho các gen nằm trên nhiễm sắc thể thường. Ngoài ra định luật cũng đòi hỏi hai điều kiện nữa là:

- Các gen phân chia một cách bình thường vào trong các hợp tử;

- Tần số gen của con đực và con cái là như nhau.

Mối quan hệ giữa tần số gen và tần số kiểu gen trong một quần thể theo định luật Hardy-Weinberg được minh hoạ trong hình 1.1.

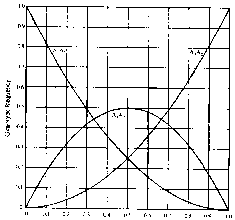
Tần số gen A2

Hình 1.1. Mối quan hệ giữa tần số kiểu gen và tần số gen của hai allen trong quần thể tuân theo định luật Hardy-Weinberg

Đồ thị tần số kiểu gen cho thấy:

- Tần số dạng dị hợp không bao giờ vượt quá 50%, tần số lớn nhất xảy ra khi tần số các gen là: p = q = 0,5.

- Khi một allen có tần số thấp, allen đó chủ yếu có trong dạng dị hợp và có rất ít trong dạng đồng hợp. Điều nhận biết này rất quan trọng trong chọn lọc.

2.2. Chứng minh định luật Hardy - Weinberg

Bốn bước và những điều kiện cần của định luật Hardy - Weinberg được tóm tắt như

Bước Từ ... đến ... Điều kiện

Tần số gen ở đời bố mẹ (1) Phân chia gen bình thường

1a (2) Sinh sản như nhau ở đời bố mẹ

Tần số gen ở toàn bộ (3) Khả năng thụ tinh như nhau ở giao tử 1b các giao tử

Tần số gen ở các giao tử (4) Quần thể lớn

2 hình thành nên hợp tử (5) Phối giống ngẫu nhiên

Tần số kiểu gen ở hợp tử (6) Tần số gen như nhau ở bố và mẹ

3 (7) Khả năng sống như nhau

Tần số kiểu gen ở đời con

Tần số gen ở đời con

Bước 1: Từ tần số gen của bố mẹ tới tần số gen của giao tử Giả sử quần thể bố mẹ có tần số gen và kiểu gen như sau:

Gen Kiểu gen

A1		A2			A1 A1	A1A2		A2A2
Tần số	p		q			P	H		Q

Có 2 loại giao tử, một loại chứa gen A1, loại kia chứa gen A2. Các bè mÑ A1A1 chỉ sản sinh giao tử chứa gen A1, A2A2 chỉ sản sinh giao tử chứa gen A2, còn A1A2 sản sinh 2 loại giao tử chứa gen A1và A2 với số lượng bằng nhau. Nếu tất cả các kiểu gen có khả năng sản sinh giao tử như nhau thì tần số gen A1 trong toàn bộ các giao tử của quần thể sẽ bằng P + 1/2H. Như vậy, tần số gen trong toàn bộ các giao tử sẽ đúng bằng tần số gen của quần thể bố mẹ. Đây là bước 1a.

Tuy nhiên, chỉ có một số giao tử nhất định hình thành nên hợp tử để tạo nên các cá thể ở thế hệ con. Nếu tất các giao tử có cùng khả năng thụ tinh như nhau và những giao tử hình thành được hợp tử là đại diện cho toàn bộ các giao tử của bố mẹ thì tần số gen của hợp tử là không thay đổi. Đây là bước 1b.

Bước 2: Từ tần số gen của giao tử tới tần số kiểu gen của hợp tử

Giao phối ở quần thể bố mẹ là ngẫu nhiên, nghĩa là các giao tử kết hợp với nhau một cách ngẫu nhiên. Tần số kiểu gen của hợp tử sẽ là tích của tần số các loại giao tử mà chúng kết hợp với nhau:

Cỏc giao tử cái và tần số của chúng

	A1	A2
		p	q
Các	A1	A1A1	A1A2
giao tử đực	p	p2	pq
và tần số	A2	A1A2	A2A2
cđa chóng	q	pq	p2

Sự kết hợp giữa trứng A1 với tinh trùng A2 cũng giống như với sự kết hợp giữa trứng A2 với tinh trùng A1, do vậy tần số kiểu gen của hợp tử sẽ là:

Kiểu gen

A1A1 A1A2 A2A2

Tần số p2 2pq q2

Bước 3: Từ tần số kiểu gen của hợp tử đến tần số kiểu gen của cá thể trưởng thành

Tần số kiểu gen của các cá thể trưởng thành ở thế hệ con sẽ bằng tần số kiểu gen của hợp tử nếu như tất cả các hợp tử đều có khả năng sống như nhau.

Bước 4: Từ tần số kiểu gen của cá thể trưởng thành tới tần số gen của chúng Tần số gen của các cá thể trưởng thành được tính theo phương trình [1.1]. Tần số gen A1 sẽ là: p2 + 1/2(2pq) = p(p + q) = p

Còn tần số gen A2 sẽ là : 1 - p = q

Như vậy tần số gen ở đời con đúng bằng tần số gen ở đời bố mẹ, cứ như vậy tần số gen sẽ không thay đổi qua các thế hệ, nếu các điều kiện đã nêu được tôn trọng.

2.3. Tần số giao phối và một bằng chứng khác của định luật Hardy - Weinberg

Giả sử có hai allen tại một locus, tần số gen và kiểu gen ở bố mẹ như sau:

Gen Kiểu gen

A1		A2		A1A1		A1A2		A2A2
Tần số		p		q		P		H		Q

Như vậy sẽ có 9 kiểu giao phối, nếu là giao phối ngẫu nhiên thì tần số giao phối như

Kiểu gen và tần số của mẹ A1A1 A1A2 A2A2

P H Q

PH PQ

H2 HQ

HQ Q2

Kiểu gen A A P

1 1

và tần số A A H

1 2

cđa bè A A Q

2 2

Trên thực tế chỉ có 6 kiểu giao phối, nếu tất cả các kiểu giao phối đều có khả năng thụ tinh và tỷ lệ sống ở đời con như nhau thì kiểu gen ở đời con như sau:

Phối giống Kiểu gen và tần số ở đời con

Kiểu	Tần số		A1A1 P	A1A2 H	A2A2 Q
2 2 A1A1 x A1A1 P P - -
A1A1 x A1A2	2PH	PH		PH	-
A1A1 x A2A2 A A x A A	2PQ H2	- 1/4H2		2PQ 1/2H2	- 1/4H2
A1A2 x A2A2	2HQ	-		HQ	HQ
A A x A A	Q2		-	-	Q2

1 2 1 2

2 2 2

Céng (P+1/2H)2 2(P+1/2H)(Q+1/2H) (Q+1/2H)2

= p2 2pq q2

Trong bảng trên, kiểu giao phối A1A1 x A1A1 chỉ cho đời con có kiểu gen A1A1, đóng

góp một tỷ lệ là P2 trong tổng số kiểu gen A A ở đời con. Kiểu giao phối A A x A A sẽ

1 1 1 2 1 2

cho 1/4 đời con có kiểu gen là A A

đóng góp một tỷ lệ 1/4H2 trong tổng số loại kiểu gen

1 1

A1A1 ở đời con. Các tính toán khác tương tự như vậy. Cuối cùng, cộng tần số từng kiểu gen ở đời con ta lại thấy xuất hiện cân bằng Hardy - Weinberg ở đời con.

2.4. Một số ứng dụng của định luật Hardy - Weinberg

2.4.1. Tìm tần số gen của allen lặn

Dựa vào phương trình [1.1] ta có thể tính được tần số gen của một nhóm cá thể khi biết tần số kiểu gen của cả 3 dạng của chúng. Như vậy ta không thể tính được tần số gen trong trường hợp allen lặn, bởi vì ta không phân biệt được dạng dị hợp và đồng hợp trội. Tuy nhiên, không cần phải biết tần số của cả 3 kiểu gen, ta vẫn xác định được tần số gen. Chẳng hạn, a là gen lặn có tần số là q, do đó tần số dạng đồng hợp aa là q2, còn tần số gen là căn bậc hai của tần số dạng đồng hợp.