b. Hai dao động điều hoà khác tần số với tỷ lệ giữa hai tần số là số hữu tỷ
Cho hai dao động điều hoà thực hiện chuyển động dọc theo hai trục toạ độ vuông góc với nhau có dạng
x t = Asin ω1t + α1; y t = Bsin ω2 t + α2(2.35)
với
ω1 T2
=
ω2 T1
p
= ≠ 1 (p, q = 1,2,3, … . )
q
Có thể bạn quan tâm!
-
Dao động kỹ thuật - 1 -
Dao động kỹ thuật - 2 -
Các Thí Dụ Về Thiết Lập Phương Trình Vi Phân Dao Động -
Xác Định Các Tham Số Độ Cứng Của Hệ Dao Động -
Tính Toán Dao Động Tự Do Có Ma Sát Nhớt
Xem toàn bộ 182 trang tài liệu này.
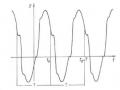
Trong trường hợp này quĩ đạo là những đường cong phức tạp nội tiếp trong một hình chữ nhật cạnh là 2A và 2B và được gọi là các đường cong Lissajou. Hình dạng của chúng phụ thuộc vào tỷ số ω1/ω2 và hiệu số của các pha ∆α = α2 − α1. Trên hình
1.13 là đường cong Lissajou khi ω1: ω2 = 2: 3 và ∆α = α2 − α1 = 0.
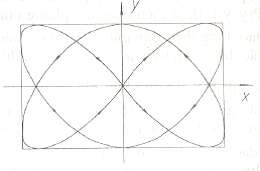
Hình 1.13 Đường cong Lissajou khi 𝜔1: 𝜔2 = 2: 3 và ∆𝛼 = 𝛼2 − 𝛼1 = 0
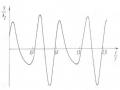
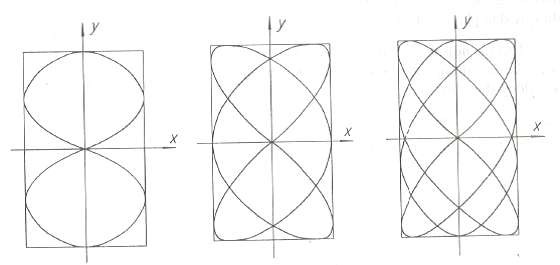
Người ta chứng minh được rằng tỷ số ω1/ω2 bằng tỷ số cực đại các múi của đường Lissajou dọc theo các trục Ox và Oy. Trên hình 1.14 là đồ thị các đường Lissajou với ∆α = 0, T1/T2 lần lượt là 1/2, 2/3 và 3/4.
Dựa vào hình dạng các đường Lissajou ta có thể xác định được chu kỳ của một
dao động thành phần khi biết chu kỳ dao động của thành phần kia. Các đường cong Lissajou được sử dụng nhiều trong kỹ thuật do dao động.
𝑇1 1
=
𝑇2 2
𝑇1 2
=
𝑇2 3
𝑇1 3
=
𝑇2 4
Hình 1.14 đồ thị các đường Lissajou
1.2.6 Biểu diễn dao động tuần hoàn trên mặt phẳng pha
Giả sử y(t) là một đại lượng dao động. Khi đó đạo hàm của y(t) theo thời gian, ký hiệu là y (t), cũng là một đại lượng dao động. Ta có thể xem y(t), y (t) là cách biểu diễn dạng tham số của hàm y (y). Ta chọn hệ trục toạ độ vuông góc với trục hoành là y, trục tung là y . Đồ thị của hàm y (y) trong hệ toạ độ vuông góc đó được gọi là quỹ đạo pha hay đường cong pha. Mặt phẳng (y, y ) được gọi là mặt phẳng
y
t0
t1
t2
t3
O
y
.
Hình 1.15 Điểm ảnh trên quỹ đạo pha
pha. Trong mặt phẳng pha, dao động được mô tả bởi sự di chuyển của điểm ảnh P(y, y ). Biểu diễn trên mặt phẳng pha ta không thấy được quá trình tiến triển của dao động theo thời gian. Để khắc phục nhược điểm này, người ta gắn vào vị trí của các điểm ảnh trên quỹ đạo pha một thông tin phụ về thời gian (hình 1.15).
Điểm ảnh P(y, y ) cho biết giá trị tức thời của đại lượng dao động y và đạo hàm của nó theo thời gian ý ở thời điểm t. Ưu điểm của sự biểu diễn dao động trên mặt phẳng pha là từ dạng hình học của quỹ đạo pha ta có thể rút ra những kết luận quan trọng về tính chất của đại lượng dao động. Nếu đại lượng dao động là tuần hoàn thì quỹ đạo pha là đường cong kín.
Trường hợp đơn giản của dao động tuần hoàn là dao động điều hoà. Từ phương trình dao động điều hoà
y = Asin ωt + α
y = ωAcos(ωt + α)
.
A
y
-A
A
b)
-A
y
y
+A
.
y
-A
+A
-A
a)
Hình 1.16 Các quỹ đạo pha của dao động điều hoà
Khử t ta được phương trình quỹ đạo pha dao động điều hoà
y 2 y
+
2
= 1 (2.36)
A ωA
Phương trình (2.36) biểu diễn trên mặt phẳng pha một elip với các bán trục là A và ωA (hình 1.16a). Nếu chọn tỷ xích trên các trục hoành và trục tung một cách thích hợp thì quỹ đạo pha của dao động điều hoà là đường tròn (hình 1.16b).
Đối với một số quá trình dao động tuần hoàn ta rất khó biểu diễn phương trình quỹ đạo pha y = f(y) dưới dạng giải tích. Trong trường hợp đó ta phải vẽ quỹ đạo pha bằng cách tính các trị số y(tk) và y (tk) với k = 0, 1, 2,…,n. Ngày nay với sự phát triển của tin học việc vẽ các quỹ đạo pha khá thuận tiện và đơn giản.
Để làm thí dụ ta vẽ quỹ đạo pha dao động răng cưa trong thí dụ 1.1 với các gần đúng n = 1, 2, 3. Từ thí dụ 1.1 ta có
n
2h 1
2kπt
n
4h 2kπt
ynt = −
sin π k
k=1
; y nt = −
T
cos
T T
k=1
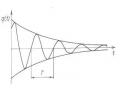
Từ đó ta vẽ được các quỹ đạo pha với n = 1, 2, 3 như trên hình 1.17. Với n = 1 ta có quỹ đạo pha dao động điều hoà. Với n = 2 và n = 3 ta có quỹ đạo pha dao động tuần hoàn.
Chú ý rằng ở nửa trên của mặt phẳng pha do y > 0 nên hàm y tăng. Các điểm ảnh chuyển động trên quỹ đạo pha từ trái sang phải. Ở nửa dưới mặt phẳng pha do y < 0 nên các điểm ảnh chuyển động từ phải qua trái.
Nếu biết được phương trình quỹ đạo pha y = f(y) thì ta tính được hàm ngược giữa t và y
y
dy dy
dt = → t = t0 + (2.37)
f(y) f(y)
y0
Đối với các dao động tuần hoàn, ta có thể tìm được chu kỳ dao động T bằng cách tích phân theo hệ thức (2.37) trên toàn bộ quỹ đạo pha kín. Đối với dao động điều hoà thì từ phương trình (2.36) ta có
y = ω A2 − y2
Do đó ta tính được chu kỳ dao động theo hình 1.16
A
dy 2
A
y 2π
T = 2=
ω A2 − y2
−A
arcsin =
ω A ω
−A
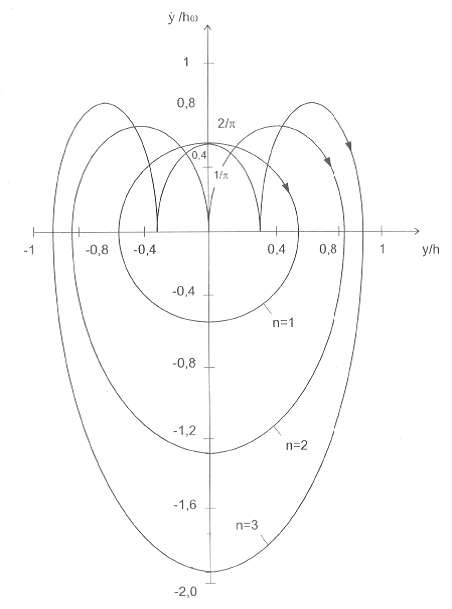
Hình 1.17 Các quỹ đạo pha của dao động mô tả bởi hàm răng cưa
1.3 DAO ĐỘNG KHÔNG TUẦN HOÀN
1.3.1 Tổng hợp hai dao động điều hoà cùng phương khác tần số với tỷ lệ giữa hai tần số là số vô tỷ
Trong phần trên ta đã thấy tổng hợp hai dao động điều hoà cùng phương khác tần số với tỷ lệ giữa hai tần số là số hữu tỷ ω1: ω2 = p: q là dao động tuần hoàn chu kỳ T = pT1 = qT2. Bây giờ ta xét bài toán
y t = y1t + y2t = A1 sin ω1t + α1+ A2 sin ω2t + α2(3.1)
Trong đó tỷ số ω1: ω2 là một số vô tỷ. Dao động tổng hợp y(t) không phải là dao động tuần hoàn vì bội số chung nhỏ nhất của T1 = 2π/ω1, và T2 = 2π/ω2 không tồn tại. Tuy nhiên ta có thể biểu diễn
ω1 p
=
ω2 q
+ ε (3.2)
với ε bé tuỳ ý. Khi đó ta chọn T ≈ pT1 ≈ qT2, dao động tổng hợp là hàm hầu tuần hoàn. Chú ý rằng hàm y(t) gọi là hàm hầu tuần hoàn nếu với 𝜂 > 0 cho trước bé tuỳ ý tồn tại một hằng số T* mà y t + T∗− y(t) < 𝜂. Vậy tổng hợp hai dao động điều hoà cùng phương khác tần số với tỷ lệ giữa hai tần số là số vô tỷ ta được dao động hầu tuần hoàn.
Thí dụ 1.2: Tổng hợp hai dao động điều hoà cùng phương với tỷ lệ hai tần số là
ω1: ω2 = 22 , A1 = A2, α1 = α2 = 0.
Lời giải: Dao động tổng hợp là
yt= A sin ω1t + A sin 2ω1t (3.3)
Chú ý đến hệ thức lượng giác sinα + sinβ = 2sin α+β cos α−β, biểu thức (3.3)
2 2
có dạng y t = 2Asin 1+ 2ω t cos 1− 2ω
t (3.4)
2 1 2 1
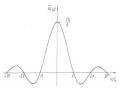
Trên hình 1.18a là quá trình diễn biến dao động theo thời gian với A = 1 và
ω1 = 2πs−1. Chu kỳ của các dao động thành phần là T1 = 1 s, T2 = 22 s .
Trên hình 1.18b biểu diễn tiến trình dao động trên biểu đồ véc tơ phức, còn trên hình 1.18c là tiến trình dao động biểu diễn trên mặt phẳng pha. Trên các hình này, các đường cong biểu diễn dao động không tuần hoàn là các đường cong không kín. Quỹ đạo pha cho ta thấy tính không tuần hoàn của dao động rò hơn trên đồ thị diễn biến dao động theo thời gian.
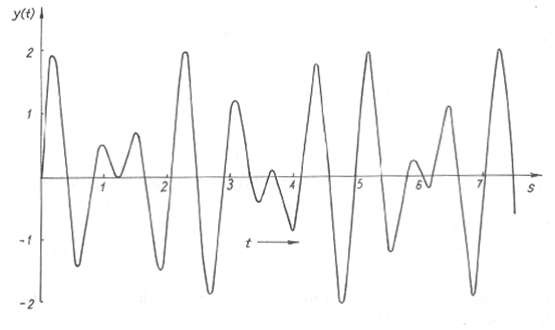
Hình 1.18a Quá trình diễn biến dao động theo thời gian
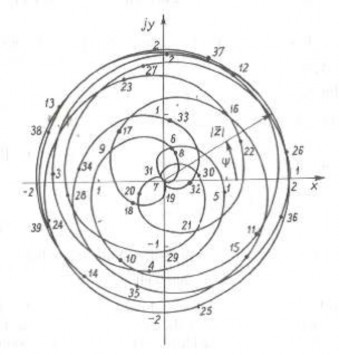
Hình 1.18b Tiến trình dao động trên biểu đồ véc tơ phức
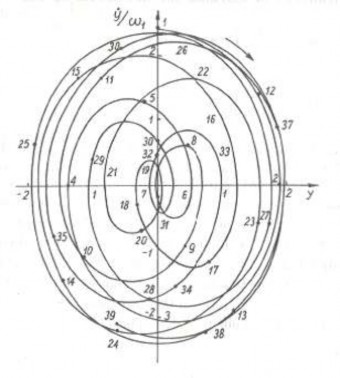
Hình 1.18c Tiến trình dao động biểu diễn trên mặt phẳng pha
1.3.2 Biểu diễn tích phân Fourier các hàm không tuần hoàn
Như chúng ta đã biết một hàm tuần hoàn có thể biểu diễn qua các hàm điều hoà bằng chuỗi Fourier. Vấn đề đặt ra ở đây là có thể biểu diễn hàm không tuần hoàn y(t) qua các hàm điều hoà với một số khái niệm suy rộng nào đó về chuỗi Fourier được hay không?
Giả sử y(t) là một hàm xác định trên toàn bộ trục số, trong một đoạn hữu hạn hàm y(t) liên tục hoặc có thể có một số hữu hạn điểm gián đoạn và hàm y(t) tuyệt đối khả tích. Điều đó có nghĩa là tích phân suy rộng
∞
I = y(t) dt (3.5)
−∞
tồn tại và có giá trị hữu hạn. Khi đó trong toán học đã chứng minh được rằng hàm y(t) có thể biểu diễn dưới dạng tích phân Fourier như sau
∞
y t = a ω cosωt + b ω sinωt dω (3.6)
−∞
Trong đó các hàm a(ω) và b(ω) được xác định bởi các hệ thức
a ω1
2π
yτcosωτdτ
(3.7)
b ω =
∞
1
y τ sinωτdτ
2π
−∞
So sánh cách biểu diễn bằng chuỗi Fourier các hàm tuần hoàn với cách biểu diễn bằng tích phân Fourier các hàm không tuần hoàn ta thấy có sự tương tự giữa công thức (2.18) với (3.6), giữa công thức (2.19) với (3.7). Trong đó chu kỳ T → ∞, mật độ phổ rời rạc xác định bởi hệ thức (2.19) thay bằng mật độ phổ liên tục xác định bởi (3.7). Tuy nhiên trong (2.19) các đại lượng ak và bk là các biên độ của các thành phần cosin và sin ứng với tần số ωk = kω của điều hoà thứ k. Đơn vị của chúng trùng với đơn vị của đại lượng dao động y(t). Trong (3.7) các hàm a(ω) và b(ω) được gọi là mật độ phổ, hay gọi tắt là mật độ. Đơn vị của chúng bằng đơn vị của đại lượng dao động y(t) nhân với đơn vị thời gian.
Biểu thức
A ω = a2ω + b2(ω) (3.8)
được gọi là phổ mật độ biên độ hay gọi tắt là mật độ biên độ. Bình phương của mật độ biên độ
A2ω = a2ω + b2ω (3.9)
được gọi là phổ mật độ công suất hay gọi tắt là mật độ công suất. Chú ý rằng cách gọi này trong một số tài liệu không được thống nhất. Có tài liệu gọi A(ω) và A2(ω) là phổ biên độ và phổ công suất. Cách gọi ấy thật ra không được chính xác.
Nếu y(t) là hàm chẵn hoặc hàm lẻ, thì biểu diễn tích phân Fourier của y(t) sẽ đơn giản hơn nhiều. Nếu y(t) là hàm chẵn, do y(-t) =y(t) nên b(ω)=0 và
a ω =
∞
1
y τ cosωτdτ (3.10)
π
0
Biểu thức (3.8) có dạng
A ω = a(ω) (3.11)
Nếu y(t) là hàm lẻ, y(-t) = -y(t), ta có a ω = 0 và
∞
b ω =
Từ đó suy ra
1
y τ sinωτdt (3.12)
π
0
A ω = b(ω) (3.13)
Trong nhiều bài toán ứng dụng người ta cũng hay sử dụng cách biểu diễn tích phân Fourier dạng phức. Từ hệ thức
∞ ∞ ∞ ∞
1
y t =
2π
dω
1
y τ eiω(t−τ)dτ =
2π
eiωt dω y τ e−iωτ dτ (3.14)
−∞ −∞
ta suy ra
∞
−∞ −∞
Trong đó
y t = A ω eiωt dω (3.15)
−∞
∞
A ω = 1
2π
y τ e−iωτ dτ
−∞
= a ω − ib ω = A(ω) e−iφ(ω) = A ω e−iφ ω (3.16)
Đại lượng A ω gọi là phổ mật độ biên độ phức, A(ω) như trên đã gọi là mật độ biên độ thực, φ ω = arctg b(ω)/a(ω) là phổ pha.
y(t)
C
Thí dụ 1.3: Cho y(t) là hàm va chạm lý tưởng, được biểu diễn bởi phương trình sau (hình 1.19a)
y t = c khi t < t0
0 khi t ≥ t0
Hãy xác định mật độ biên độ phức
A ω , mật độ công suất A2 (ω) và cách biểu t0
O t0 t
diễn tích phân của hàm y(t).
Hình 1.19a Đồ thị hàm y(t)
Lời giải: Hàm y(t) là hàm thoả mãn các điều kiện về hàm khả tích tuyệt đối. Vì vậy ta có thể biểu diễn hàm này dưới dạng tích phân Fourier.
Do y(t) là hàm chẵn nên b ω = 0, ta có
Do tgφ ω = 0 nên có thể lấy φ ω = 0. Từ đó suy ra