Ví dụ 95. Vẽ đồ thị ellipse x2 + y2
= 1 (Hình 3.8)
4 9
> implicitplot((1/4) ∗ x2 + (1/9) ∗ y2 = 1, x = −2..2, y = −3..3, title =′
Ellipse′);
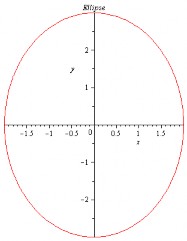
Hình 3.8: Ellipse
- Để vẽ mặt cong bậc hai ta dùng lệnh implicitplot3d.
2
4
9
Ví dụ 96. Vẽ mặt yên ngựa x2 − y
= 2z (Hình 3.9)
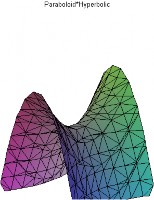
Hình 3.9: Paraboloid Hyperbolic
Bảng 3.1: Bảng trị riêng và vector riêng của ma trận đặc biệt
Trị riêng λ | Vector riêng e | |
Ma trận đối xứng A = AT | ∀λ ∈ R | eT ej = 0 i |
Ma trận trực giao AT = A−1 | ∀|λ| = 1 | eiT ej = 0 |
Ma trận phản đối xứng thực AT = −A | ∀λ thuần ảo | eiT ej = 0 |
T Ma trận Hermite (phức) A = A | ∀λ ∈ R | eiT ej = 0 |
Ma trận xác định dương xT Ax > 0 | ∀λ > 0 | eiT ej = 0 |
Ma trận đồng dạng B = M −1AM | λA = λB | eA = M eB |
Ma trận chiếu P = P 2 = P T | λ = 1; 0 | K.gian sinh bởi các cột; KerP |
Ma trận hạng 1 tức A = uvT | λ = vT u; 0, ..., 0 | u; Toàn bộ k.gian u⊥ |
Ma trận nghịch đảo A−1 | 1/λA | Giữ nguyên vector riêng của A |
Ma trận dịch chuyển A + cE | λA + c | Giữ nguyên vector riêng của A |
Có thể bạn quan tâm!
-
Cơ Sở Trực Chuẩn, Quá Trình Trực Chuẩn Hóa Gram-Schmidt -
, Ct Ac = -
Đại số tuyến tính và Hình học giải tích - Hy Đức Mạnh - 16
Xem toàn bộ 141 trang tài liệu này.
Tài liệu tham khảo
[1] Lê Tuấn Hoa. Đại số tuyến tính qua các ví dụ và bài tập // NXB ĐHQGHN. 2005. 406T.
[2] Nguyễn Đình Trí (Chủ biên). Toán cao cấp. Tập 1. Đại số tuyến tính và hình học giải tích // NXB GD. 1997.
[3] Nguyễn Xuân Viên. Đại số tuyến tính // NXB Học viện KTQS. 2014. 252T.
[4] Nguyễn Xuân Viên (Chủ biên). Bài tập đại số tuyến tính và hình học giải tích // NXB QĐND. 2010. 251T.
[5] A. R. G. Heesterman. Matrices and Their Roots: A Textbook of Matrix Algebra // WS. 1990. 444p.
[6] G. Hadley. Linear Algebra // Addison-Wesley Publishing Company, INC. 1961. 290p.
[7] S. Lang. Linear Algebra. Third Edition // Springer. 2004. 296p.
[8] D. Serre. Matrices: Theory and Applications // Springer. 2002. 219p.
[9] G. Strang. Introduction to Linear Algebra, 4th, Wellesley-Cambridge Press. 2009. 574p.
[10] Maple Getting Started Guide. Copyright ⃝c Waterloo Maple Inc. 2005.
Maplesoft, a division of
[11] Ï.Ñ. Àëåêđàíäđîâ. Êóđđ àíàëẹ̀è÷åđêîé ăåî́ạ̊đèè è ëèíåéíîé àëăåáđû //Èçä. Íàóêà. 1979. 511c.
[12] Èëüèí Â.À., Ïîçíÿê Ư.Ă. Àíàëẹ̀è÷åđêàÿ ăåî́ạ̊đèÿ // Èçä. Íàóêà. 1999. 223đ.
[13] Èëüèí Â.À., Ïîçíÿê Ư.Ă. Ëèíåéíàÿ àëăåáđà // Èçä. Íàóêà. 1999. 294c.
[14] Ô.Đ. Ăàị́́àơåđ. ̉åîđèÿ ̀ạ̀đèö // Èçä. Íàóêà. 1966. 576đ.
[15] È. ̀. Ăåëüôàíä. Ëåêöèè ïî ëèíåéíîé àëăåáđå // Èçä. Íàóêà. 1974. 271c.
[16] ̀àëüöåâ À.È. Îđíîâû ëèíåéíîé àëăåáđû, ̀., Íàóêà 1970. 400đ.
Index
Biến đổi sơ cấp, 40 Biểu đồ Venn, 15
Bất biến, 83
Cauchy-Bunhia-Schwartz, 107
Chiều, 60
Chuẩn, 107
Chéo hóa, 85, 117
Chéo hóa trực giao, 114 Công thức Cramer, 49 Công thức De Morgan, 16 Công thức Moivre, 24 Công thức Viet, 28
Cơ sở, 60
Cơ sở chính tắc, 64 Cơ sở trực chuẩn, 108
Dạng chính tắc, 97 Dạng cực, 93
Dạng song tuyến tính, 93 Dạng toàn phương, 93
Giao, 15
Gram-Schmidt, 108
Hermite, 115
Hessian, 105
Hiệu, 15
Hiệu đối xứng, 15 Hình chiếu, 114
Hạng hệ hữu hạn vector, 60
Hạng ma trận, 38 Hệ Cramer, 49
Hệ phương trình tuyến tính, 47 Hệ sinh, 62
Hệ thuần nhất, 48, 78
Hợp, 15
Khai triển Taylor, 27
Không gian Euclide, 93, 105 Không gian hữu hạn chiều, 63 Không gian nghiệm, 58, 78 Không gian tổng và giao, 67 Không gian vector, 57
Không gian vector con, 59
Lagrange, 99
Logic, 11
Lược đồ Horner, 28 Lực lượng, 19, 20
Ma trận, 30
Ma trận chuyển vị, 33 Ma trận chính tắc, 77 Ma trận hình thang, 40 Ma trận khả nghịch, 41 Ma trận suy biến, 36
Ma trận trực giao, 34, 110 Ma trận tương đương, 82 Ma trận đường chéo, 34 Ma trận đối xứng, 34
Ma trận đồng dạng, 82
Maple, 52, 91
Minkowski, 107
Nghiệm riêng, 52 Nghiệm tổng quát, 52 Nhân, 72, 96
Nhóm, 21
Nhóm Abel, 22, 58
Phân tích LU , 44 Phân tích LU P , 44 Phân tích QR, 112 Phép chia Euclide, 25
Phương trình vi phân, 58 Phương trình đặc trưng, 84, 117
Phần bù, 16
Phổ, 85, 119
Phụ thuộc tuyến tính, 60 Pythagore, 108
Quan hệ hai ngôi, 17 Quan hệ thứ tự, 17
Quan hệ tương đương, 17 Quy tắc đổi dấu Descartes, 29 Quán tính, 101, 102
Siêu mặt bậc hai, 122 Song ánh, 19, 20
Sylvester, 102
Số phức, 23
Toàn cấu, 76
Toàn cấu, 73
Toàn ánh, 19, 20
Toán tử tuyến tính, 69 Toán tử tự liên hợp, 114 Trường, 21
Trị riêng, 83
Trực giao, 96, 108
Tích Descartes, 17 Tích vô hướng, 105 Tập hợp, 14
Tổ hợp tuyến tính, 60 Tổng trực tiếp, 69
UCLN, 26
Vector, 31, 57
Vector riêng, 83
Vành, 21
Vành giao hoán, 22 Vành đa thức, 25 Vô hướng, 57
Xác định dương, 103 Xác định âm, 103
Ánh xạ, 19
Ánh xạ ngược, 20
Ánh xạ tuyến tính, 57, 69 Ánh xạ tuyến tính ngược, 75
Đa thức đặc trưng, 84 Đơn cấu, 73, 76
Đơn ánh, 19
Đẳng cấu, 76, 136
Đẳng hướng, 96 Định lý Bezout, 27
Định lý Cronecker-Capelli, 51, 79 Định lý Laplace, 38
Định lý Sylvester, 104 Định thức, 34
Đồng dư, 18
Độ dài, 107
Độc lập tuyến tính, 60
Độc lập tuyến tính tối đại, 61 Ảnh, 72