Trong các trị riêng λ1, ..., λn, giả sử có r giá trị khác 0, và không sợ nhầm lẫn, ta vẫn ký hiệu các giá trị khác 0 đó là λ1, ..., λr, khi đó (3.10) có thể viết lại dưới dạng
r r
i
∑ λit2 + 2 ∑ diti + e = 0 (3.11)
i=1 i=1
Nếu ta tịnh tiến điểm gốc O sang I (vẫn trong cơ sở {e′1, ..., e′n}) như sau
ti
Có thể bạn quan tâm!
-
Đại số tuyến tính và Hình học giải tích - Hy Đức Mạnh - 13 -
Cơ Sở Trực Chuẩn, Quá Trình Trực Chuẩn Hóa Gram-Schmidt -
, Ct Ac = -
Đại số tuyến tính và Hình học giải tích - Hy Đức Mạnh - 17
Xem toàn bộ 141 trang tài liệu này.
= zi
di
i
− λ , i = 1; r
ti = zj , j = r + 1; n
thì trong cơ sở (e′) gốc I mới, phương trình siêu mặt có dạng
∑ λiz +
n
r
2
i
i=1
i=∑r+1
c′zi + d′ = 0, 1 ≤ r ≤ n, λi ̸= 0 (3.12)
i) Nếu c′i = 0, i = r + 1; n và d′ ̸= 0 khi đó (3.12) có dạng I.
ii) Nếu c′i = 0, i = r + 1; n và d′ = 0 khi đó (3.12) có dạng II.
iii) Nếu r < n và tồn tại c′i ̸= 0, i = r + 1; n, ví dụ c′r+1 ̸= 0. Đặt
p = t
uu∑
v n
j=r+1
c′i2, gi =
c′i
, i = r + 1; n
p
ta đưa siêu mặt về dạng
∑λiz + 2p
r
2
i
∑
i=1
n i=r+1
gizi +
d′
)
= 0 (3.13)
2p
( ∑
ở đó các gi thỏa mãn
i
K như sau
n
i=r+1
g2 = 1. Tiếp tục xét phép đổi gốc mới từ I sang
n
∑i=r+1
d′ gizi − 2p
yi= zi, i = i = 1; r
yr+1 = −
yr+1 = −
yj=
n
∑
gjkzk, j = r + 1; n
k=r+1
ở đó gjk được chọn sao cho ma trận phép đổi biến này vẫn là ma trận trực giao (để đảm bảo cơ sở mới vẫn là trực chuẩn). Khi đó siêu mặt sẽ có dạng
r
i
∑ αiy2 = 2pyr+1, αi = −λi, 1 6 r 6 n (3.14)
i=1
Đây chính là dạng III. Ta có điều phải chứng minh. I
Sau đây ta đưa ra tên gọi của một số siêu mặt bậc hai:
i) Siêu mặt có dạng I với r = n với các αi > 0, i = 1; n, gọi là siêu mặt Ellipsoid n − 1-chiều. Phương trình này có thể viết lại dưới dạng
∑
n 2
xi = 1
a2
i=1 i
ii) Siêu mặt có dạng I với r = n với các αi, i = 1; n, khác dấu nhau gọi là siêu mặt Hyperboloid và có thể viết lại dưới dạng
∑
i ∑
k 2 n2
x xj
a2 − a2 = 1
i=1 i j=k+1 j
iii) Siêu mặt bậc hai có phương trình dạng II với r = n và các hệ số
αi, i = 1; n, mang dấu khác nhau gọi là siêu mặt nón (thực).
iv) Siêu mặt bậc hai có phương trình dạng III với r = n − 1 và các hệ số αi, i = 1; n − 1, cùng dấu gọi là siêu mặt Paraboloid Elliptic, còn các hệ số αi, i = 1; n − 1, có dấu khác nhau gọi là siêu mặt Paraboloid Hyperbolic.
v) Siêu mặt bậc hai có phương trình dạng I, II với r < n và dạng III với
r < n − 1 gọi là các siêu mặt trụ (Elliptic, Hyeperbolic, Parabolic...)
Cũng phải chú ý rằng đôi khi các siêu mặt suy biến thành một điểm, hoặc tập rỗng (còn gọi là siêu mặt ảo).
3.5.2 Phân loại các đường cong và mặt cong bậc hai
Đường cong bậc hai trên mặt phẳng
Trong trường hợp không gian Euclide n = 2 chiều ta có các đường cong bậc hai trên mặt phẳng Euclide, và n = 3 ta có các mặt cong bậc hai trong không gian Euclide. Chúng ta hiểu mặt phẳng hoặc không gian Euclide như là các không gian tọa độ thực trên đó có trang bị tích vô hướng, mỗi vector đồng nhất với một điểm, vector 0 đồng nhất với gốc O. Chúng ta thường sử dụng hệ truc tọa độ trực chuẩn Descartes (đã quen thuộc ở bậc học dưới) để mô tả trong trường hợp hai hoặc ba chiều. Trên không gian đó có thể xây dựng các khái niệm khoảng cách, góc... như đã nói trong các bài trước. Đường bậc hai tổng quát trên mặt phẳng với hệ tọa độ trực chuẩn
Descartes Oxy có dạng
a11x2 + 2a12xy + a22y2 + a1x + a2y + c = 0 (3.15)
(
)
ở đó các hệ số a11, a12, a22 không đồng thời bằng 0. Ma trận của dạng toàn phương là A = AT có thể đưa về dạng chéo bằng biển bổi trực giao, nghĩa là tồn tại ma trận C sao cho
CT AC = λ1 0
0 λ2
( )
ở đó C là ma trận trực giao. Vì C là cấp hai nên nó chỉ có một trong hai dạng trong ví dụ đã đưa ra ở bài chéo hóa trực giao, ta chọn
C = cosφ − sin φ
sin φ cosφ
và xét phép đổi biến
y
sin φ cos φ
y′
( x ) = ( cos φ − sin φ ) ( x′ )
Ta có thể đưa dạng toàn phương về dạng chính tắc
λ1x′2 + λ2y′2
Phép đổi biến ở trên thực chất là quay hệ tọa độ ban đầu đi một góc φ và khi đó đường bậc hai có dạng
λ1x′2 + 2λ2y′2 + a′1x′ + a′2y′ + c = 0 (3.16)
Tiếp tục sử dụng phép tịnh tiến gốc ta có thể đưa về một trong các loại sau đây
1) Ellipse (hoặc đường tròn)
2) Hyperbola
3) Ellipse ảo
x2
a2 +
x2
a2 −
y2
b2 = 1
y2
b2 = 1
x2
a2 +
y2
b2 = −1
4) Cặp đường thẳng ảo cắt nhau (tại một điểm thực)
x2
a2 +
y2
b2 = 0
5) Cặp đường thẳng cắt nhau
x2
a2 −
y2
b2 = 0
6) Parabola
x2 = 2py
7) Cặp đường thẳng song song
x2
a2 = 1
8) Cặp đường thẳng ảo song song
x2
a2 = −1
9) Cặp đường thẳng trùng nhau
x2
a2 = 0
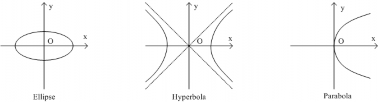
Hình 3.3: Các đường Conic
Các đường bậc hai Ellipse, Hyperbola, Parabola là những đường Conic đã được học trong bậc học phổ thông.
Mặt cong bậc hai trong không gian
Trong không gian hệ tọa độ trực chuẩn Decartes Oxyz mặt bậc hai tổng quát là tập các điểm thỏa mãn phương trình đại số
a11x2 + 2a12xy + 2a13xz + a22y2+ 2a23yz + a33z2+ 2a1x + 2a2y + 2a3z + c = 0.
(3.17)
Xét dạng toàn phương với ma trận là A = (aij )3×3, ở đó A = AT . Tồn tại ma trận chuyển cơ sở C để
λ10 0
0
0 0 λ3
CT AC = 0 λ2
0 0 λ3
0 0 λ3
Ma trận C là ma trận trực giao, có thể chọn C sao cho det(C) = 1, ví dụ
cos φ − sin φ 0
Phép đổi biến
C = sin φ cos φ 0
0 0 1
x x′
y=C y′
z
z′
z
z′
là phép quay hệ trục tọa độ đi một góc φ. Mặt cong khi đó có dạng
λ1x′2 + λ2y′2 + λ3z′2 + 2a’1x′ + 2a′2y′ + 2a′3z′ + c = 0 (3.18)
Tịnh tiến gốc tọa độ nếu cần ta sẽ đưa mặt bậc hai về một trong các dạng sau
1) Ellipsoid (cầu)
x2 y2 z2
2) Ellipsoid ảo
a2 + b2 + c2 = 1
x2 y2 z2
3) Nón ảo
a2 + b2 + c2 = −1
x2 y2 z2
4) Hyperboloid 1 tầng
a2 + b2 + c2 = 0
x2 y2 z2
a2 + b2 − c2 = 1
5) Hyperboloid 2 tầng
x2 y2 z2
6) Nón Elliptic
a2 +
b2 − c2 = −1
x2 y2 z2
7) Paraboloid Elliptic
a2 + b2 − c2 = 0
x2 y2
a2 + b2 = 2z
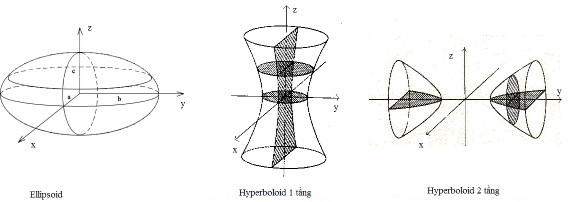
Hình 3.4: Mặt Elipsoid và Hyperboloid 1, 2 tầng
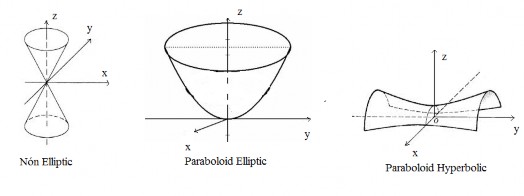
Hình 3.5: Nón Elliptic, Paraboloid Elliptic, Paraboloid Hyperbolic
8) Paraboloid Hyperbolic (yên ngựa)
9) Trụ Elliptic
x2
a2 −
x2
y2
b2 = 2z
y2
10) Trụ Elliptic ảo
a2 +
b2 = 1
11)Trụ Parabolic
x2
a2 +
y2
b2 = −1
12) Trụ Hyperbolic
y2 = 2px
x2
a2 −
13) Cặp mặt phẳng ảo liên hợp
x2
a2 +
y2
b2 = 1
y2
b2 = 0
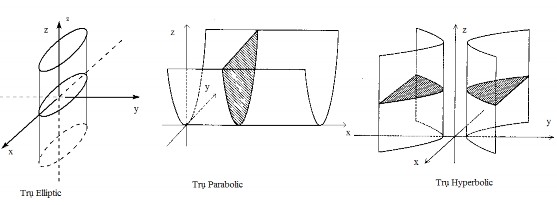
Hình 3.6: Các mặt trụ
14) Cặp mặt phẳng cắt nhau
x2
a2 −
y2
b2 = 0
15) Cặp mặt phẳng thực song song
x2
a2 = 1
16) Cặp mặt phẳng ảo song song
x2
a2 = −1
17) Cặp mặt phẳng trùng nhau
x2
a2 = 0
3.6 Thực hành tính toán trên Maple
Như các chương trước chúng ta vẫn làm việc trong môi trường linalg.
- Để tính tích vô hướng của hai vector u, v ta dùng lệnh dotprod(u, v);
hoặc dotprod(u, v, orthogonal);
- Tìm cơ sở trực giao của không gian vector sinh bởi một họ các vector bằng lệnh GramSchmidt({v1, v2, ...});
Ví dụ 93.
> v1 := vector([1, 2, 3]);
v1 := [1 2 3]
> v2 := vector([−1, 0, −2]);
v1 := [−1 0 − 2]
> v3 := vector([2, 1, −3]);
> dotprod(v1, v2);
v3 := [2 1 − 3]
−7
> GramSchmidt(v1, v2, v3);
2
2
7
7
7
{[1, 2, 3] , [−1, 1, −1], [20, 5− 10]}
Để vẽ đồ thị đường cong và mặt cong trong Maple ta cần dùng gói lệnh
plots.
- Vẽ đồ thì hàm số y = f (x) ta dùng lệnh có cú pháp
> plot(f (x), x = a..b, y = c..d,title=’tiêu đề’);
Ví dụ 94. Vẽ đồ thị hàm số y = x3 − 2x
> restart;
> with(plots);
> plot(x3 − 2 ∗ x, x = −2..3, y = −5..10, title =′ Hambacba′);
Ta có kết quả trên Hình 3.7.
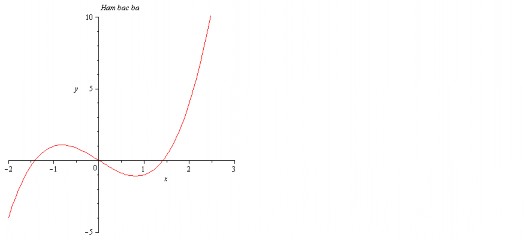
Hình 3.7: Đồ thị hàm bậc ba
- Vẽ đồ thị hàm ẩn f (x, y) = 0 dùng cú pháp lệnh
> implicitplot(f (x, y) = 0, x = a..b, y = c..d);