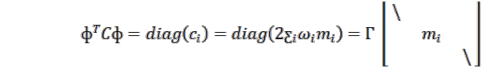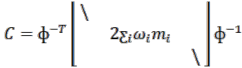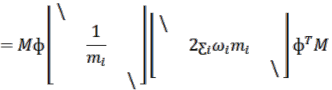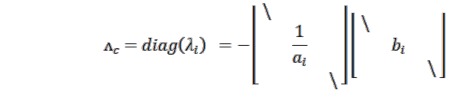Tình Hình Nghiên Cứu Ở Việt Nam Về Giám Sát Sức Khỏe Kết Cấu Công Trình

trên các kỹ thuật GD (Gradient Descent), có một nhược điểm chính liên quan đến các vấn đề cực tiểu cục bộ, đặc biệt có thể xảy ra khi mạng chứa các bề mặt lỗi khác nhau với nhiều cực tiểu cục bộ được phân phối rộng rãi.

1.3. Tình hình nghiên cứu ở Việt Nam về giám sát sức khỏe kết cấu công trình dựa trên phương pháp đo nhận dạng dao động‌

Ở Việt Nam, các nghiên cứu về lĩnh vực giám sát sức khỏe kết cấu công trình đầu tiên tập trung vào phát hiện các vết nứt tồn tại trong kết cấu, sau đó các nghiên cứu tiếp tục đi vào phân tích sự phát triển của các vết nứt. Các nghiên cứu về phát hiện hư hỏng trong kết cấu được thực hiện với nhiều loại kết cấu như cầu đường, các loại nền móng và các giàn khoan. Nguyễn Tiến Minh [66] đề xuất phương pháp xác định sự thay đổi của các tham số trong kết cấu cầu như mô đun đàn hồi của bê tông bằng cách so sánh kết cấu ở trạng thái chưa hư hỏng và trạng thái hư hỏng. Tuy nhiên trong nghiên cứu này chưa đề cập đến khả năng phát hiện khu vực cũng như mức độ hư hỏng của kết cấu.

Bùi Đức Chính [67-70] sử dụng biến đổi Hilbert-Huang để chẩn đoán hư hỏng của kết cấu phần dưới của công trình cầu. Kết quả chứng minh rằng biến đổi Hilbert- Huang có thể phân biệt được các ứng xử dao động khác nhau của các trụ cầu, ngoài ra còn có thể xác định được sự giảm về độ cứng của các trụ, trong khi đó các phương pháp biến đổi cũ như Fast Fourier Transform (FFT), và Wavelet Transform (WT) chỉ cho thấy có sự thay đổi nhỏ về biên độ dao động của các trụ cầu, nhưng không thể đưa ra được mức độ của sự thay đổi biên độ này. Ngoài ra các phương pháp chuyển đổi như FFT và WT còn chịu ảnh hưởng khá nhiều của hiện tượng nhiễu. Ngô Trọng Đức và cộng sự [71] áp dụng phân tích các dao động riêng để xác định các vết nứt trong các dầm sử dụng vật liệu có cơ tính biến thiên. Trong nghiên cứu này, ảnh hưởng của nhiễu cũng được xem xét. Kết quả chỉ ra rằng, phương pháp đề xuất có thể phát hiện được vị trí của vết nứt.

Khiêm và cộng sự [72] đề xuất phương pháp phân tích tần số riêng của kết cấu dầm với một số vết nứt ngẫu nhiên dựa trên phương pháp ma trận chuyển giao và mô hình lò xo quay của các vết nứt. Phương pháp đề xuất có thể xác định chính xác khu vực hư hỏng và giảm thời gian tính toán so với các phương pháp khác. Phạm Xuân Khang [73-76] đề xuất thuật toán để xác định các hư hỏng trong kết cấu dựa vào các đặc trưng động học (so sánh dao động riêng của kết cấu ở các trạng thái đo khác nhau).

Nghiên cứu đề xuất được áp dụng cho công trình cầu thực tế và đem lại những kết quả phù hợp với thực tế. Tác giả cũng áp dụng phương pháp động dựa vào sự thay đổi của dạng dao động riêng để đề xuất trình tự chẩn đoán hư hỏng trong kết cấu nhịp giản đơn. Nguyễn Việt Khoa [77-82] đã áp dụng các phương pháp giám sát sức khỏe không phá hủy dựa vào đặc trưng động học của kết cấu để chẩn đoán các hư hỏng trong kết cấu.

Một số nghiên cứu cũng đã được tiến hành để giám sát sức khỏe cho các công trình cầu lớn như cầu Mỹ Thuận, cầu Bãi Cháy, hay cầu Kiền bằng cách lắp đặt các thiết bị cảm ứng để theo dòi thường xuyên sức khỏe kết cấu công trình. Tuy nhiên, những thiết bị này chỉ cung cấp các thông tin cơ bản và cần được kiểm chứng cũng như so sánh với các mô hình tính toán bằng cách áp dụng cập nhật mô hình từ đó xác định các tham số chưa tường minh hoặc thay đổi trong quá trình khai thác hay tác động của ảnh hưởng môi trường như tính chất vật liệu, độ cứng của các bộ phận, điều kiện biên,...từ đó đánh giá đúng khả năng chịu lực cũng như chẩn đoán các hư hỏng xảy ra nếu có của công trình.

Nguyễn Hữu Thuấn và cộng sự [83] giám sát sức khỏe cầu dây văng Mỹ Thuận bằng cách tiến hành đo thực nghiệm tại hiện trường. Một mô hình số cũng được xây dựng để so sánh với kết quả từ thực nghiệm. Hàm mục tiêu so sánh bao gồm tần số dao động riêng và hình dạng dao động. Bùi Tiến Thành và cộng sự [84] tiến hành đo đạc thực nghiệm cầu dây văng Mỹ Thuận. Tuy nhiên trong nghiên cứu này, tác giả tập trung vào lựa chọn vị trí tối ưu của các cảm biến để có thể thu nhập được nhiều thông tin nhất về các đặc trưng động học của kết cấu như tần số dao động riêng và hình dạng dao động. Hoàng Nam [85] nghiên cứu về hệ thống quan trắc để lắp đặt cho cầu Cần Thơ nhằm thu thập các dữ liệu về tần số dao động riêng và hình dạng dao động. Bùi Xuân Ngó và cộng sự [86] xác định một số chỉ tiêu kỹ thuật cơ bản của cầu dây văng thông qua các hệ thống quan trắc sức khỏe kết cấu công trình theo thời gian thực. Nguyễn Trọng Nghĩa và cộng sự [87] đo lực căng dây cáp của cầu dây văng Phú Mỹ dựa trên phương pháp đồ thị. Lực căng cáp được tính toán dựa vào kết quả đo dao động, bao gồm tần số dao động riêng. Trần Văn Đức và cộng sự [88] thực hiện các phép đo hiện trường để xác định các đặc trưng động học của cầu dây văng Phò Nam.

Các nghiên cứu về giám sát sức khỏe kết cấu công trình bằng nhận dạng dao động đã thực hiện ở Việt Nam chủ yếu phân tích hoặc xác định các đặc trưng động học

của kết cấu như tần số dao động riêng, hình dạng dao động...mà chưa hoàn toàn xác định được giá trị của các thông số bất định của kết cấu có thể thay đổi theo thời gian như các đặc trưng của vật liệu (mô đun đàn hồi...), hình dạng mặt cắt, và điều kiện biên. Những thông số này ảnh hưởng đến sự làm việc của kết cấu và phản ánh rò ràng nhất những ứng xử của kết cấu khi xảy ra hư hỏng. Ngoài ra, mặc dù gần đây trên thế giới các nghiên cứu sử dụng các thuật toán tối ưu, hay các phương pháp học máy đã được áp dụng rộng rãi và hiệu quả để giám sát sức khỏe các công trình. Ở Việt Nam, các kỹ thuật này vẫn còn mới, chưa có nhiều nghiên cứu sử dụng các thuật toán tối ưu, hay các phương pháp học máy để giám sát sức khỏe các công trình.

Kết luận Chương 1‌

Chương 1 giới thiệu tổng quan về giám sát sức khỏe kết cấu công trình dựa trên phương pháp đo nhận dạng dao động và tình hình nghiên cứu, áp dụng phương pháp giám sát sức khỏe kết cấu công trình dựa trên phương pháp này. Hiện nay, việc giám sát sức khỏe các công trình cầu ở Việt Nam theo các định kỳ thời gian nhất định, áp dụng các phương pháp tĩnh, phụ thuộc nhiều vào sự phán đoán của các kỹ sư. Các phương pháp này đòi hỏi chi phí lớn, huy động nhiều nhân lực, độ chính xác hạn chế cũng như không kịp thời chẩn đoán các hư hỏng hoặc sự cố xảy ra với các công trình. Giám sát sức khỏe kết cấu công trình dựa trên các đặc trưng động học như tần số dao động riêng, hình dạng dao động và hệ số cản là phương pháp giám sát sức khỏe không phá hủy. Phương pháp này có nhiều ưu điểm điển hình như: cung cấp một cách thức toàn cục để đánh giá trạng thái kết cấu, các phép đo tại một địa điểm là đủ để đánh giá tình trạng của toàn bộ kết cấu, các kết cấu vẫn có thể khai thác trong điều kiện bình thường khi tiến hành các công tác thực nghiệm.

CHƯƠNG 2: NGHIÊN CỨU VÀ ĐỀ XUẤT PHƯƠNG PHÁP CHẨN ĐOÁN HƯ HỎNG KẾT CẤU BẰNG PHƯƠNG PHÁP ĐO‌

DAO ĐỘNG NGẪU NHIÊN

2.1. Cơ sở lý thuyết về dao động kết cấu‌

Dao động của kết cấu liên tục được rời rạc hóa bằng phương pháp phần tử hữu hạn với số bậc tự do- (degree-of-freedom-DOF) được thể hiện bởi phương trình vi phân bậc hai viết dưới dạng ma trận (còn được gọi là phương trình chuyển động cơ bản) [27]:

(2.1)

Có thể bạn quan tâm!

Xem toàn bộ 154 trang tài liệu này.

Ở đây , 𝐾 lần lượt là ma trận khối lượng, ma trận giảm chấn, ma trận độ cứng của kết cấu; 𝑢(𝑡) là véc tơ chuyển vị tại thời điểm 𝑡 (biến thời gian liên tục) bất kỳ. Véc tơ và và véc tơ (hàm) vận tốc và gia tốc. Véc tơ 𝑓(𝑡) biểu diễn lực tác dụng, là tổng hợp của ma trận vị trí và véc tơ lực tác dụng vào phần tử

𝑢(𝑡). Ma trận khối lượng 𝑀 và ma trận độ cứng 𝐾 được xây dựng từ đặc trưng hình học và đặc trưng vật liệu của kết cấu. Cách xây dựng ma trận giảm chấn thường dựa vào quan sát hiện tượng vật lý hoặc dựa trên các giả thuyết toán học để đơn giản hóa việc mô tả bài toán dao động tắt dần (ví dụ như trường hợp mô tả giảm nhớt theo quy luật hàm mũ âm).

Trên thực tế, giảm chấn là hiện tượng vật lý rất phức tạp. Do đó, tổng hợp được ma trận giảm chấn cho kết cấu thực là rất khó khăn thậm chí là không thể trong phần lớn các công trình. Mô hình phần tử hữu hạn ở phương trình (2.1) là cách phổ biến nhất để mô tả hình thức dao động của kết cấu. Tuy nhiên xét về phương diện dao động, nó chỉ là công cụ khởi đầu để diễn tả những khái niệm phức tạp hơn của các mô hình phù hợp cho công tác thí nghiệm. Lý do thứ nhất là không thể đo đạc được hết tất cả các bậc tự do (mô hình tính toán một kết cấu quy mô lớn có thể bao gồm hàng triệu phần tử, trong đó có rất nhiều phần tử không thể gắn được thiết bị đo đạc). Thứ hai, 𝑡 trong phương trình 2.1 là biến liên tục, trong khi đó số liệu đo là các mẫu rời rạc theo thời gian. Thêm vào đó nhiễu và sai số là một phần không thể thiếu được trong bất kỳ thí nghiệm động nào. Cuối cùng thì kết cấu có thể dao động do các tác động không thể đo đạc được như gió và các yếu tố ngẫu nhiên khác.

2.1.1. Bài toán giá trị riêng cho kết cấu dao động không tắt

Đầu tiên ta xét trường hợp kết cấu dao động không tắt. Lời giải cho bài toán tìm giá trị riêng và véc tơ riêng ở phương trình (2.1) được trình bày ở đây để diễn giải cho các khái niệm cơ bản ở các phần sau. Khi không có ma trận giảm chấn và không có ngoại lực tác dụng, phương trình (2.1) có dạng phần tử hữu hạn dao động tự do như sau:

(2.2)

(2.3)

Chuyển vị của kết cấu xác định bằng phương pháp giải tích có dạng: . Thay thế lại phương trình 2.2 ta được phương trình trị riêng tổng quát:

Ở là bất kỳ véc tơ trị riêng và là giá trị riêng (số thực). Trong trường hợp không giảm chấn, giá trị riêng thường được định nghĩa là bình phương của tần số , do đó:

(2.4)

Ở đây 𝑗 là phần ảo của số phức đơn vị = −1. Tất cả bài toán giá trị riêng ở (2.3) có thể được viết lại dưới dạng:

(2.5)

Ở đây ф chứa véc tơ trị riêng theo các cột và ѱ= diag ) là ma trận đường chéo chứa các tần số riêng [rad/s]. Có thể chứng minh rằng điều kiện trực giao sau đây được thỏa mãn :

(2.6)

Ở đây là các phần tử khối lượng mode (modal masses) và là các phần tử độ cứng mode (modal stiffness). Vector là vector chuyển vị của vector . Thay phương trình (2.6) vào (2.5) ta được:

(2.7)

Véc tơ trị riêng được xác định khi đồng nhất phương trình (2.6) về ma trận khối lượng hình thức đơn vị:

(2.8)

Ở đây 𝐼 là ma trận đơn vị có kích thước . Véc tơ trị riêng còn được gọi là véc tơ mode (modal vector) và trong phân tích hình thức dao động kết cấu nó được

nhắc tới như là các hình dạng dao động, bởi vì đặc trưng của véc tơ này rất trực quan và dễ hiểu để mô tả biến dạng của kết cấu. Chú ý rằng nếu kết cấu dao động liên tục thì véc tơ trị riêng có giá trị thực và cũng được gọi là véc tơ mode tiêu chuẩn (normal modal vector).

2.1.2. Dao động tắt dần tỷ lệ

Bằng cách nhân hai vế của phương trình chuyển động cơ bản (2.1) và chuyển hệ tọa độ ta có:

(2.9)

(2.10)

Véc tơ ∈ chứa các giá trị chuyển vị mode (modal displacements). Tính trực giao ở phương trình (2.6) có thể dùng để rút gọn phần tử thứ nhất và phần tử thứ ba ở vế trái của phương trình (2.9). Trong trường hợp tắt dần ta có thể biến đổi ma trận giảm chấn thành dạng đường chéo . Sau đó bằng cách định nghĩa tỷ lệ giảm dao động và đặt Г=diag(2 ta có:

Thay phương trình (2.6) và (2.10) vào (2.9) ta được:

(2.11)

Nghiệm của phương trình vi phân bậc hai thuần nhất (mô hình phần tử hữu hạn viết dưới dạng ma trận) có dạng . Có thể dễ dàng nhận thấy rằng véc tơ trị riêng có dạng giống như trường hợp dao động không tắt. Giá trị riêng của phương trình (2.11) phải thỏa mãn phương trình:

(2.12)

Cho ta đáp số:

(2.13)

Ở đây ‘*’ ký hiệu số phức liên hợp. Khi dùng phương pháp phần tử hữu hạn để phân tích động, ta thường phải xác định các tỷ lệ giảm dao động riêng (modal damping ratio) tương ứng với số mode dao động cần thiết. Các hệ số này có thể xác

định từ kết quả đo dao động. Cuối cùng ma trận giảm chấn tổng hợp từ phương trình (2.10) có dạng:

2 14 Chú ý rằng đẳng thức thứ hai được biến đổi từ điều kiện trực 49

(2.14)

Chú ý rằng đẳng thức thứ hai được biến đổi từ điều kiện trực giao như ở phương trình (2.6). Trường hợp đặc biệt của giảm dao động tắt dần tỷ lệ là giảm chấn Rayleigh theo đó ma trận giảm chấn tỷ lệ thuận với ma trận khối lượng và ma trận độ cứng:

(2.15)

Với 𝛼 và 𝛽 là hằng số. Nhìn vào phương trình này ta thấy thêm một điều kiện ràng buộc vào hệ phương trình phần tử hữu hạn. Tuy nhiên bản chất vật lý của nó là ma trận hệ số giảm dao động được phân bố tỷ lệ trên toàn bộ kết cấu. Như đã đề cập, rất khó có thể kết luận về cơ chế giảm dao động, do đó ta phải dựa vào các giả thiết gần đúng và có ý nghĩa toán học để thuận tiện cho việc phân tích.

2.1.3. Dao động giảm nhớt tổng quát

Nếu như giả thiết về giảm dao động tỷ lệ không còn đúng nữa như trường hợp kết cấu cầu dây có gắn thiết bị giảm chấn, ta phải dùng cách khác để xác định giá trị riêng – đó là lý thuyết giảm nhớt tổng quát (general viscous damping). Trên thực tế gần như tất cả các phương pháp thực nghiệm để tìm ra hệ số giảm dao động thường sử dụng lý thuyết giảm nhớt. Trong trường hợp không giảm tỷ lệ, véc tơ trị riêng của phương trình dao động không tắt (2.2) không giống với véc tơ trị riêng của phương trình dao động có cản. Để giải bài toán giảm nhớt, phương trình dao động tổng quát (2.1) phải được viết lại dưới dạng bậc nhất bằng cách đặt:

(2.16)

Khi đó (2.1) trở thành:

(2.17)

Ở đây 𝑥(𝑡) được gọi là véc tơ trạng thái (state vector). Bài toán trị riêng có dạng:

(2.18)

Trong đó chứa = vector riêng phức theo cột và = )

∈là ma trận đường chéo bao gồm giá trị riêng phức [rad/s]. Có thể nhận thấy rằng và Ѱ có dạng như sau:

(2.19)

Ở đây ʌ, ∈ là giá trị riêng và véc tơ riêng của phương trình vi phân bậc hai ban đầu. Phương trình (2.18) thỏa mãn điều kiện:

(2.20)

Chú ý rằng ký hiệu thay thế ký hiệu của trường hợp giảm chấn tỷ lệ, giá trị riêng có dạng như sau:

(2.21)

Có thể chứng minh được rằng điều kiện trực giao sau đây được thỏa mãn:

(2.22)

Ở đây ), ) được gọi là ma trận mode và ma trận mode . Thay thế phương trình (2.22) vào phương trình (2.18) ta được:

(2.23)

2.2. Các phương pháp chẩn đoán hư hỏng kết cấu dựa trên dao động‌

2.2.1. Phương pháp dựa trên sự thay đổi của tần số dao động riêng‌

Cách tiếp cận phổ biến nhất và sớm nhất để xác định hư hỏng trong kết cấu dựa vào dao động đó là việc sử dụng tần số dao động riêng hoặc cộng hưởng của kết cấu. Sự xuất hiện của hư hỏng trong kết cấu gây nên những sự thay đổi của tần số riêng trong kết cấu. Một nghiên cứu chuyên sâu sử dụng dữ liệu tần số riêng để xác định các hư hỏng trong kết cấu được cung cấp bởi [28, 89]. Ndambi và cộng sự [90] biểu diễn một thí nghiệm kiểm tra để đánh giá sự tương hợp giữa quá trình phát triển vết nứt trong dầm bê tông cốt thép. Tải trọng tĩnh được sử dụng để tạo ra các vết nứt trong dầm và thí nghiệm động được sử dụng để xác định các đặc trưng động học của kết cấu. Mỗi thí nghiệm tĩnh được đi kèm với một thí nghiệm động trên cùng một mẫu dầm với

Xem tất cả 154 trang.

Ngày đăng: 14/07/2022