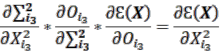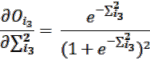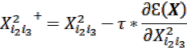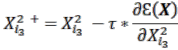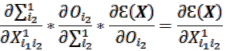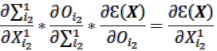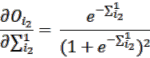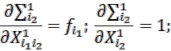Chẩn Đoán Hư Hỏng Kết Cấu Dựa Trên Kết Quả Đo Nhận Dạng Dao Động Sử

2.4. Chẩn đoán hư hỏng kết cấu dựa trên kết quả đo nhận dạng dao động sử dụng mạng nơ ron nhân tạo.‌

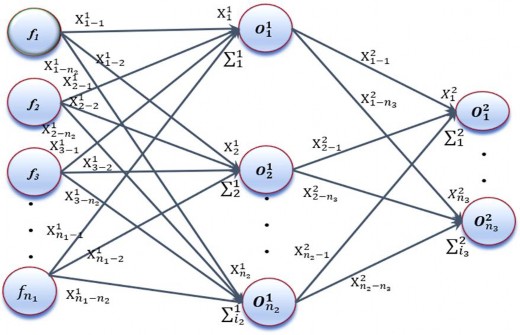
Phương pháp học máy, cụ thể ANN – là các chương trình máy tính lấy cảm hứng từ hệ nơ ron sinh học được thiết kế để mô phỏng theo cách mà bộ não con người xử lý thông tin. ANN thu thập kiến thức bằng cách phát hiện các mẫu và mối quan hệ trong dữ liệu thông qua học tập từ kinh nghiệm, không phải từ lập trình. Mạng nơ-ron nhân tạo được hình thành từ rất nhiều đơn vị nơ-ron nhân tạo, được kết nối với các hệ số (trọng số) tạo thành kết cấu nơ ron. Một mạng nơ ron cơ bản bao gồm một lớp đầu vào, một lớp đầu ra, một hoặc nhiều lớp ẩn được thể hiện như hình 2.2.

Hình 2.2. Kiến trúc mạng ANN

Có thể bạn quan tâm!

Xem toàn bộ 154 trang tài liệu này.

Các nơ-ron trong các lớp được kết nối với nhau bằng các tham số huấn luyện (trọng lượng và độ lệch). Lớp ẩn bao gồm một số đơn vị xử lý nhất định và đóng vai trò quan trọng là cầu nối giữa lớp đầu vào và lớp đầu ra. Mỗi phần tử trong các lớp trước được kết nối đầy đủ với các phần sau và các kết nối dựa trên các tham số đào tạo (trọng lượng và độ lệch). Việc truyền tín hiệu dựa trên hai phương trình. Phương trình đầu tiên là hàm tổng ). Hàm số này phụ thuộc vào các tham số huấn luyện (trọng số và độ lệch) và giá trị đầu ra của các lớp trước đó, tức là:

(2.37)

là các hệ số trọng số và độ lệch kết nối lớp đầu vào và lớp ẩn, trong khi là dữ liệu đầu vào của nơ-ron thứ ; trong đề tài này chính là tần số dao động riêng của các mode dao động; và lần lượt là số nơ-ron trong lớp đầu vào và lớp ẩn; biểu thị đầu vào của nơ-ron thứ của lớp ẩn.

Sau khi hàm tổng (phương trình 2.37) được tiến hành, phương trình thứ hai là hàm kích hoạt được áp dụng để giới hạn phạm vi giá trị của các đầu ra. Hàm kích hoạt có thể là hàm tuyến tính hoặc phi tuyến tăng đơn điệu. Có bốn loại chính của hàm kích hoạt bao gồm là hàm step, hàm ramp, hàm sigmoid và hàm Gaussian. Hàm sigmoid thường được sử dụng vì nó có thể xử lý nhiều vấn đề phức tạp liên quan đến các hàm phi tuyến. Các giá trị đầu ra ) thu được bằng cách sử dụng hàm sigmoid như trong phương trình 2.38.

(2.38)

Quá trình chuyển các nơ-ron từ lớp ẩn sang lớp đầu ra tương tự như quá trình chuyển nơ ron từ lớp đầu vào sang lớp ẩn, sử dụng phương trình 2.39 và 2.40

(2.39)

đầu vào của nơ ron của lớp đầu ra; là số nơ ron của lớp đầu ra,

(2.40)

Trong ML nói chung và ANN nói riêng, chúng ta thường xuyên phải tìm giá trị nhỏ nhất (hoặc đôi khi là lớn nhất) của một hàm số nào đó. Nhìn chung, việc tìm tối ưu toàn cục (global best) của các hàm mất mát trong ML là rất phức tạp. Hướng tiếp cận phổ biến nhất là xuất phát từ một điểm mà chúng ta coi là gần với nghiệm của bài toán, sau đó dùng một phép toán lặp để tiến dần đến điểm cần tìm, tức đến khi đạo hàm gần với 0. Trong đó, hàm độ dốc đi xuống (Gradient Descent - GD) là phương pháp được dùng phổ biến trong ML.

Về cơ bản, đào tạo một mạng là thay đổi tỷ lệ trọng lượng và độ lệch (thông số đào tạo) để giảm thiểu sự khác biệt giữa các đầu ra tính toán và mong muốn như phương trình 2.41

X1 1313

2 k1 Nk

(2.41)

NkO O

và là các đầu ra dự đoán và tính toán của dữ liệu đầu ra thứ , tương ứng. là số lượng dữ liệu đầu ra. Nếu đầu ra được tính toán vẫn khác biệt đáng kể so với đầu ra mong muốn, quy trình tính toán ngược được tiến hành bằng cách sử dụng thuật toán truyền ngược (backpropagation) dựa trên hàm GD để tính toán lại các tham số đào tạo, được mô tả như các phương trình 2.42-2.50.

(2.42)

(2.43)

(2.44)

;

(2.45)

Các tham số huấn luyện mới kết nối giữa lớp ẩn và lớp đầu ra sẽ thu được như phương trình 2.46.

(2.46)

Các thông số huấn luyện kết nối lớp đầu vào và lớp ẩn cũng được điều chỉnh; là tốc độ học.

(2.47)

(2.48)

(2.49)

(2.50)

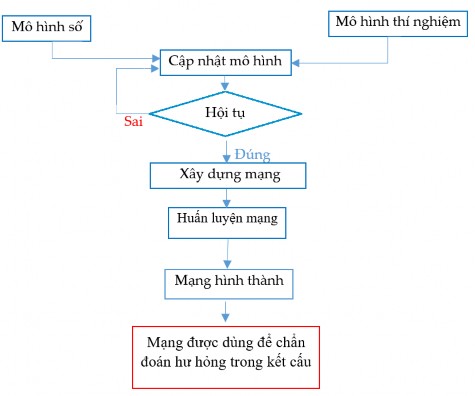
Quá trình này lặp lại cho đến khi chênh lệch giữa đầu ra thực và mong muốn là nhỏ nhất được mô tả như hình 2.3:

Hình 2.3. Sơ đồ thuật toán ANN

ANN có một số ưu điểm sau đây: khả năng xử lý rộng rãi số lượng dữ liệu lớn, thời gian huấn luyện mạng nhanh, kết quả của bước sau luôn tốt hơn bước trước nếu mạng không bị rơi vào tối ưu cục bộ.

Bên cạnh đó, còn một số nhược điểm đó là cần phải tạo được khối lượng dữ liệu đủ lớn để mạng có thể học được các quy luật, nếu dữ liệu để học tập quá ít, mạng được xây dựng sẽ không cung cấp được các kết quả chính xác và sẽ mất khả năng khái quát

hóa. Hơn nữa việc áp dụng thuật toán truyền ngược, ANN có thể bị rơi vào vùng tối ưu cục bộ nếu bài toán có quá nhiều tối ưu cục bộ. Từ đó giảm tính chính xác của kết quả sau khi huấn luyện mạng.

2.5. Chẩn đoán hư hỏng kết cấu dựa trên kết quả đo nhận dạng dao động sử dụng thuật toán kết hợp PSO-ANN.‌

ANN được áp dụng rộng rãi cho nhiều lĩnh vực. Tuy nhiên, bởi vì ANN sử dụng các thuật toán lan truyền ngược (BP) dựa trên phương pháp GD để giảm sự khác biệt giữa mục tiêu dự đoán và mục tiêu thực, mạng có thể bị mắc kẹt trong tối ưu cục bộ nếu các bề mặt lỗi phức tạp chứa quá nhiều giải pháp tối ưu cục bộ. Điều này giảm hiệu quả và độ chính xác của ANN. Atakulreka và cộng sự [134] cho rằng các thuật toán học tập dựa vào độ dốc bao gồm cả thuật toán truyền ngược, thay đổi trọng số kết nối của mạng bằng cách sử dụng tập huấn luyện bao gồm các cặp dữ liệu đầu vào và dữ liệu đầu ra mà không sử dụng bất kỳ kiến thức nào trước có thể dẫn đến mạng bị rơi vào tối ưu cục bộ. Hamid và cộng sự [135] chỉ ra rằng thuật toán truyền ngược là mô hình phổ biến được sử dụng trong các phương pháp học máy. Thuật toán này sử dụng thuật toán giảm độ dốc nhằm giảm thiểu sự sai lệch giữa kết quả tính toán và kết quả mong muốn bằng cách di chuyển xuống độ dốc của đường cong. Do thuật toán truyền ngược sử dụng thuật toán giảm độ dốc nên dễ dàng bị mắc kẹt ở tối ưu cục bộ nếu các bề mặt lỗi phức tạp với quá nhiều điểm tối ưu cục bộ. Nawi và cộng sự [136] cũng kết luận rằng các phương pháp dựa trên nguyên tắc giảm độ dốc là một trong những phương pháp giảm thiểu độ lệch giữa kết quả thực tế và kết quả mong muốn đang được sử dụng rộng rãi để huấn luyện các mạng truyền ngược trong phương pháp học máy.

Các phương pháp đào tạo mạng dựa trên thuật toán truyền ngược là một phương pháp học có giám sát đối với các mạng nơ ron chuyển tiếp nhiều lớp. Nó thực chất là một kỹ thuật tối ưu để giảm thiểu sự khác biệt giữa kết quả tính toán và kết quả mục tiêu. Mặc dù sự chênh lệch này được giảm rò rệt sau mỗi bước lặp, một số vấn đề vẫn cần được giải quyết. Kết quả hội tụ của thuật toán lan truyền ngược phụ thuộc rất nhiều vào điểm khởi tạo ban đầu, cụ thể là sự lựa chọn các giá trị ban đầu của tham số huấn luyện bao gồm tham số trọng lượng (weight) và tham số điều chỉnh (bias). Nếu điểm bắt đầu của mạng nằm khác phía và bị ngăn cách với giải pháp tối ưu toàn cục bởi các giải pháp tối ưu cục bộ (thung lũng lòm), nó có thể rơi vào các tối ưu cục bộ

thay vì tối ưu toàn cục. Hình 2.4 minh họa quá trình xác định giải pháp tối ưu toàn cục của ANN dựa vào phương pháp GD. Ở hình 2.4 (a), xét hàm số

chỉ có một điểm tối ưu toàn cục ), thì dù điểm bắt đầu từ (A) hay (B), thì tối ưu toàn cục ) luôn có thể xác định được, ở hình 2.4 (b), hàm bao gồm 1 tối ưu cục bộ ) và tối ưu toàn cục ( ), nếu điểm bắt đầu là điểm (A) thì điểm tối ưu toàn cục ) cũng sẽ được xác định chính xác. Tuy nhiên, nếu điểm bắt đầu từ điểm ), mạng sẽ chỉ xác định được giải pháp tối ưu cục bộ ) thay vì điểm tối ưu toàn cục ).

(a)

(b)

Hình 2.4. Quá trình xác định giải pháp tối ưu dựa trên phương pháp GD của ANN

(a) mạng với một điểm tối ưu toàn cục, (b) mạng với tối ưu toàn cục và cục bộ

Để giải quyết vấn đề tối ưu cục bộ và nâng cao hiệu quả của ANN, nhiều nhà nghiên cứu cũng đã đưa ra các giải pháp khác nhau. Ví dụ, Tran-Ngoc và cộng sự.

[137] đã sử dụng thuật toán tìm kiếm chim cúc cu (CS) để cải thiện hiệu quả của ANN bằng cách xác định các thông số huấn luyện ban đầu. Kết quả cho thấy sự kết hợp này vượt trội hơn ANN truyền thống và các thuật toán tối ưu hóa khác về độ chính xác. Samir và cộng sự [138] đề xuất cải thiện các thông số huấn luyện (trọng lượng và độ lệch) của ANN để phát hiện các hư hỏng trong vật liệu composite nhiều lớp. Trong nghiên cứu của họ, PSO được sử dụng để xác định điểm xuất phát tối ưu. Cách tiếp cận này đã hỗ trợ mạng trong việc tránh tối ưu cục bộ ban đầu. Tuy nhiên, vì PSO chỉ được áp dụng để xác định các tham số huấn luyện của các bước đầu tiên, mạng có thể vẫn bị mắc kẹt trong các tối ưu cục bộ khác trong các bước tiếp theo. Với cách tiếp cận tương tự, Rajendra và cộng sự. [139] đã sử dụng GA để cải thiện hiệu quả của ANN,

khi dự đoán các thông số tối ưu hóa cho sản xuất diesel sinh học. Yazdanmehr và cộng sự [140] kết hợp GA với ANN để tìm kiếm thành phần hóa học và điều kiện nghiền tối ưu để sản xuất bột tinh thể nano với độ cưỡng bức tối thiểu. Azadeh và cộng sự [141] đã sử dụng thuật toán linh hoạt dựa trên GA và ANN để đánh giá và tối ưu hóa các đơn vị sản xuất. Họ chỉ ra rằng ANN kết hợp với GA vượt trội hơn GA một mình và các phương pháp thông thường về mặt tối ưu hóa năng suất máy móc. Tuy nhiên, sự kết hợp này tốn nhiều thời gian, do GA phải điều chỉnh quá nhiều thông số trong quá trình huấn luyện. Hơn nữa, khả năng tìm kiếm toàn cục của GA cũng kém ưu việt hơn so với các thuật toán tiến hóa khác như PSO và CS [142].

Có thể dễ dàng nhận thấy rằng các cách tiếp cận nêu trên [137-141] đã áp dụng các giải pháp để loại bỏ các tối ưu cục bộ bằng cách chọn một vị trí bắt đầu có lợi bằng cách sử dụng khả năng tìm kiếm toàn cục của các thuật toán khác. Chiến lược này có thể giúp mạng tránh được tối ưu cục bộ đầu tiên (thung lũng đầu tiên). Tuy nhiên, một mạng thường có nhiều tối ưu cục bộ được phân phối khắp nơi, nếu mạng có bề mặt lỗi phức tạp ví dụ được minh họa như hình 2.5. Hàm số

có 2 tối ưu cục bộ ) và ) và một tối ưu toàn cục ), trong đó tối ưu toàn cục ) bị kẹp ở giữa 2 tối ưu cục bộ ) và ).

Hình 2.5. Mạng với nhiều tối ưu cục bộ

Trong trường hợp này, dù xuất phát từ điểm ) hay ) thì mạng vẫn bị kẹt vào tối ưu cục bộ vì tối ưu cục bộ ) và ) ngăn cản mạng tiến tới tối ưu toàn cục ). Đối với bài toán chẩn đoán ngược trong SHM, mạng thậm chí còn phức tạp hơn, với các bề mặt lòm chứa nhiều tối ưu cục bộ. Do đó, giải pháp chọn điểm xuất phát tốt có

thể không còn hiệu quả nữa vì các phần tử của mạng có thể vẫn bị mắc kẹt trong các tối ưu cục bộ tiếp theo (các thung lũng khác) trong quá trình tìm kiếm các giải pháp tối ưu. Để khắc phục những thiếu sót này, trong đề tài này, NCS đề xuất một thuật toán làm việc song song giữa ANN và PSO có thể xử lý được các hạn chế của các cách tiếp cận trước đây đã được sử dụng trong các nghiên cứu của [137-141]. Ý tưởng cốt lòi của cách tiếp cận trong đề tài này là khả năng tìm kiếm toàn cục của PSO được áp dụng để hoạt động song song với kỹ thuật GD của ANN nhằm ngăn chặn mạng kẹt trong các giải pháp tối ưu cục bộ trong suốt quá trình tìm kiếm giải pháp tối ưu thay vì chỉ chọn một vị trí bắt đầu có lợi được sử dụng trong các cách tiếp cận trước đây. Cụ thể, kỹ thuật GD đầu tiên được áp dụng để tăng tốc độ hội tụ. Phải thừa nhận rằng nếu mạng không bị mắc kẹt trong tối ưu cục bộ, các kỹ thuật GD luôn cung cấp các giải pháp của các bước tiếp theo tốt hơn các bước trước. Trong trường hợp, nếu mạng bị mắc kẹt trong các bề mặt lòm (tối ưu cục bộ), các kỹ thuật tìm kiếm toàn cục được sử dụng để giải thoát các phần tử khỏi các khu vực bất lợi đó. Quá trình này được lặp lại cho đến khi đạt được hàm mục tiêu. Hình 2.6 minh họa việc sử dụng PSO để khắc phục các vấn đề tối ưu cục bộ của ANN.

Hình 2.6. Áp dụng PSO để khắc phục vấn đề tối ưu cục bộ của ANN

Hình 2.6 xem xét hàm toán học . Hàm số này có 2 tối ưu cục bộ tại ) và ), và tối ưu toàn cục ). Trong trường hợp này dù điểm bắt đầu của mạng từ ) hay ), thì mạng sẽ bị rơi vào tối ưu cục bộ ) và ), lúc này PSO sẽ được áp dụng khi mạng bị kẹt vào các tối ưu cục bộ. PSO là phương