Cơ Sở Lý Thuyết Một Số Mô Hình Áp Dụng Trong Nghiên Cứu Cảnh Báo Vỡ Nợ

Tên

biến

Nội dung	Dấu kỳ vọng
e9	Chi phí dự phòng nợ khó đòi/Tổng thu nhập trước dự phòng và thuế	+
e10	Thu nhập từ phí dịch vụ/Tổng thu nhập hoạt động	-
e11	Lãi cận biên thuần	-
Nhóm L- Tính thanh khoản
l1	Tốc độ tăng trưởng tiền gửi	-
l2	Tốc độ tăng trưởng các khoản cho vay	+
l3	Các khoản cho vay thuần/tiền gửi của khách	+
l4	Huy động từ tổ chức kinh tế và dân cư/Tổng huy động	-
l5	Huy động trên thị trường liên ngân hàng/Tổng huy động	+
l6	Tỷ lệ tài sản lỏng/Tổng tài sản có	-
Nhóm M- Hiệu quả quản lý tài sản
m1	Thu nhập lãi thuần/tài sản cố định	-
m2	(Lợi nhuận trước thuế+dự phòng)/Chi phí hoạt động	-
m3	Thu nhập lãi thuần/ tổng tài sản có	-
m4	(Lợi nhuận trước thuế +dự phòng)/tổng tài sản có	-

Có thể bạn quan tâm!

• Các Nghiên Cứu Về Dự Báo Vỡ Nợ, Vỡ Nợ Ngân Hàng Ở Việt Nam
• Các Nhân Tố Ảnh Hưởng Tới Nguy Cơ Vỡ Nợ Của Các Ngân Hàng Thương Mại
• Xây dựng mô hình cảnh báo nguy cơ vỡ nợ đối với các ngân hàng thương mại cổ phần Việt Nam - 7
• Phương Pháp Bao Dữ Liệu (Dea) Đánh Giá Hiệu Quả Hoạt Động Của Các Nhtmcp
• Thu Chi Và Cân Đối Ngân Sách Nhà Nước (Tỷ Đồng Và %)
• Vcsh, Ta Của Một Số Định Chế Tài Chính Lớn Trong Khu Vực Asean Năm 2014

Xem toàn bộ 168 trang tài liệu này.

Nguồn: Tính toán của tác giả

Như vậy, để phân tích hoạt động kinh doanh của một ngân hàng, ta có thể sử dụng các chỉ tiêu trên. Các chỉ tiêu được phân thành các nhóm, trong mỗi nhóm có chỉ tiêu chính (Key Ratios) và chỉ tiêu hỗ trợ (supporting Ratios) và một số chỉ tiêu có thể thuộc nhiều nhóm khác nhau. Đối với một ngân hàng cụ thể các chỉ tiêu sẽ được tính toán và so sánh với các ‘ngưỡng’ từ đó đưa ra các đánh giá, xếp hạng ngân hàng. Các nhân tố mà mô hình CAMLES đề cập là cơ sở quan trọng để tác giả xây dựng hệ thống các chỉ tiêu sử dụng trong mô hình cảnh báo nguy cơ vỡ nợ các NHTMCP.

2.3. Cơ sở lý thuyết một số mô hình áp dụng trong nghiên cứu cảnh báo vỡ nợ

Phần này, tác giả trình bày cơ sở lý luận của một số mô hình cảnh báo vỡ nợ, các mô hình gồm 2 nhóm: nhóm các mô hình thống kê (mô hình Logit với dữ liệu mảng), nhóm mô hình sử dụng các kỹ thuật thông minh (ANN, DT).

2.3.1. Mô hình Logit, mô hình Logit với số liệu mảng

Mô hình Logit (LA) nghiên cứu sự phụ thuộc của một biến nhị phân vào các biến độc lập. Trong nghiên cứu cảnh báo vỡ nợ mô hình Logit có thể ước lượng xác suất vỡ nợ của một doanh nghiệp là bao nhiêu trực tiếp từ mẫu.

Mô hình Logit

Biến phụ thuộc Y, nhận một trong hai giá trị 0 hoặc 1, trong nghiên cứu cảnh báo vỡ nợ

1

0

Y 



Nếu nguy cơ vỡ nợ cao Nếu nguy cơ vỡ nợ thấp

exp(XT )

Đặt p

 p(Y  1 X )

và hàm phân bố Logistic có dạng pi i

i i i

1 exp(XT )

i

Khi Xnhận giá trị từ đến , thì p nhận giá trị từ 0 đến 1. Để ước lượng

ta dùng ước lượng hợp lý tối đa (Hosmer và cộng sự, 1989).

Mô hình LA

Mô hình PA

Đồ thị 2.1: Mô hình Logit

Ưu điểm: Mô hình Logit dễ áp dụng, có thể tiến hành nhanh chóng và việc

đánh giá hoàn toàn dựa trên cơ sở định lượng.

+ Các biến liên quan tới nguy cơ vỡ nợ dù định tính hay định lượng đều có thể được xử lý.

Nhược điểm: Trong quá trình xử lý dữ liệu mô hình LA đòi hỏi có một số lượng dữ liệu đủ lớn cho mỗi nhóm. Kết quả và khả năng phân tích, dự báo của mô hình phụ thuộc rất lớn vào nguồn thông tin thu thập được.

Mô hình Logit cho số liệu mảng

Số liệu mảng là tập số liệu thu thập được trên cùng một tập hợp các cá thể (hộ gia đình, doanh nghiệp, tỉnh, v.v…) theo thời gian tại các mốc thời điểm cách đều nhau. Số liệu mảng chứa thông tin theo chiều ngang giữa các đối tượng tại cùng một

thời điểm-đặc trưng của số liệu chéo, và thông tin theo thời gian của từng đối tượng-

đặc trưng của số liệu chuỗi thời gian.

Ta ký hiệu biến phụ thuộc là Y và các giá trị cụ thể của nó là

y it nhận giá trị 0

hoặc 1 với i  1, n

là các cá thể; t  1, Ti

là chỉ số theo thời gian của cá thể i.

x it

là véc tơ biến giải thích, là véc tơ các tham số ( các véc tơ viết dưới dạng cột)

Xét mô hình Logit với tác động cố định:

P(y

 1 x )  F( x '

) 

exp(i  x 'it )

(1.1)

it it i it

1 exp(i  x 'it )

Trong mô hình này ta giả thiết tồn tại các yếu tố không quan sát được

i và i

có tương quan với các biến giải thích trong mô hình. Tuy nhiên việc ước lượng với cùng lúc nhiều tham số trong mô hình là điều khó khăn. Các tác giả Hosmer, Lemeshow và Sturdivant (2013) đã trình bày một phương pháp ước lượng tham số 

mà không cần phải có ước lượng của các tham số

i . Phương pháp ước lượng này là

phương pháp ước lượng hợp lý cực đại dựa trên xác suất có điều kiện

Ti

T

i

 exp(yit x 'it )

P  (yi1 , yi 2 ,..., yiT ) yit  k1i t 1

i

T

(1.2)

t1

T

i

exp(dit x 'it )

diSi

t1

d it

bằng 0 hoặc 1 với

Ti



dit  k1i

t1

và Si là tập tất cả các kết hợp của

k1i và

k 2 i  Ti  k 1i .

Để đơn giản tác giả trình bày cho trường hợp Ti  2

với điều kiện

y i1  y i 2  1

Ta có: P(y

 0, y  1 y  y

 1) 

P(yi1  0, yi2  1)

(1.3)

i1 i2 i1 i2

P(y

 0, y  1)  P(y  1, y

 0)

Trong đó

i1 i2 i1 i2

P ( y i1  0 , y i 2  1)  P ( y i1  0 ) . P ( y i 2  1)

Theo công thức (1.1) ta có:

P(y

 0, y

 1) 

1  exp(i  x 'i2 )

i1 i2

1 exp( x ' ) 1 exp( x ' )

và P(y

 1, y

 0) 

exp(i  x 'i1 ) 

i i1 i i2

1

i1 i2

1 exp( x ' ) 1 exp( x ' )

i i1 i i2

Thay vào công thức (1.3) ta được:

P(y

 0, y  1 y  y

 1) 

exp(xi 2  xi1 ) '

(1.4)

i1 i 2 i1 i 2

1 exp(xi 2  xi1 ) '

Một cách tổng quát ta có thể xét đến các điều kiện

T T T

yit 1,yit  2,...,yit  T 1.

t1 t1 t1

Quá trình trên không xét các quan sát ở đó

y it  0 ,  t

hoặc

y it  1,  t .

Ước lượng được từ điều kiện cực đại hàm hợp lý

n TiTi

ln L yit x 'it  log exp(dit x 'it )

(1.5)

t1 t1 diSit1 

Lựa chọn mô hình và kiểm định sau khi ước lượng mô hình FE, RE

Để đưa ra quyết định lựa chọn giữa mô hình tác động cố định-FE hoặc mô hình tác động ngẫu nhiên-RE ta dựa vào kiểm định Hausman (1978). Ý tưởng của kiểm

định Hausman như sau nếu i

không tương quan với các biến giải thích thì cả hai

phương pháp ước lượng RE, FE đều cho kết quả ước lượng vững, do đó chúng ta kỳ vọng là các hệ số ước lượng thu được từ hai phương pháp là khá gần nhau. Còn nếu

i tương quan với các biến giải thích thì ước lượng từ mô hình FE là ước lượng vững,

trong khi đó ước lượng từ mô hình RE lại không vững, do đó các ước lượng từ hai phương pháp sẽ rất khác nhau. Kiểm định Hausman dựa trên sự khác biệt giữa các hệ số ước lượng bởi hai phương pháp để đưa ra sự lựa chọn mô hình. Cụ thể

H0 : i không tương quan với

x it

H 1 :

i có tương quan với

x it

Thống kê kiểm định là: 2 (ˆˆ )'(V  V )1 (ˆˆ )

qs FE RE FE RE FE RE

Giả sử sau khi thực hiện kiểm định Hausman và kết quả mô hình FE được lựa

^

chọn. Bước tiếp theo là ước lượng các i khi đã có kết quả ước lượng  của 

Trong trường hợp Ti nhỏ, ta xác định các các i từ điều kiện

Ti exp( x ' )

(yit  Pit )  0 trong đó

t1

Pit i it

1 exp(i  x 'it )

^ ^

1 Ti

ei.ex 'it

1 Ti

ex 'it 

1 Ti c

^

Ta có

yi 

^ 

it

i

Ti t 1 1 ei .ex 'it

Ti t1  ex 'it 

Ti t1 i  cit

Với 1 ; c exp(x '

^

) . Tính toán

và suy ra

i ei

it 

it 

i i  lo g i

Để tính tác động biên của biến

x i tới xác suất vỡ nợ p ta có công thức

 p 

i

 ln( ) 

i

1 p 

hoặc

p  p(1 p)

(1.6)

Ưu điểm:

xi

xi

+ Số liệu mảng có thể giải quyết vấn đề biến nội sinh (một vấn đề thường gặp trên thực tế) do thiếu biến không quan sát được. Lẽ dĩ nhiên bản thân số liệu mảng không giúp giải quyết được vấn đề biến nội sinh mà ở kỹ thuật ước lượng của nó.

+ Số liệu mảng giúp tăng bậc tự do, do đó làm tăng độ chính xác của các suy diễn thống kê. Ta hình dung nếu nghiên cứu n doanh nghiệp chỉ trong 1 năm thì ta sẽ chỉ có n quan sát trong khi nếu sử dụng dữ liệu trong T năm ta sẽ có n.T quan sát.

+ Phân tích số liệu mảng thích hợp với điều kiện các nước đang phát triển trong đó có Việt Nam, nơi mà hệ thống thu thập và quản lý số liệu còn hạn chế. Ở các nước này, tính ổn định trong cấu trúc của nền kinh tế thường chưa cao nên việc sử dụng chuỗi số dọc theo một khoảng thời gian dài thường là không thích hợp. Khi đó số liệu mảng xem xét được tính ổn định trong quan hệ giữa các biến số, đồng thời đảm bảo được số bậc tự do của mô hình đủ lớn.

Từ những ưu điểm của số liệu mảng, mô hình Logit và từ mục đích nghiên cứu của luận án (nghiên cứu nguy cơ vỡ nợ của các NHTMCP Việt Nam thời kỳ 2010- 2015) tác giả lựa chọn áp dụng mô hình Logit với số liệu mảng cho nghiên cứu của mình. Nghiên cứu cũng thử nghiệm áp dụng mô hình mạng nơron, cây quyết định vào phân loại, dự báo nguy cơ vỡ nợ cho các NHTMCP Việt Nam.

2.3.2. Mạng nơron

Mạng nơ ron là một mô hình dựa trên ưu thế của máy tính áp dụng nhiều trong bài toán phân loại và được sử dụng ngày càng nhiều trong nghiên cứu vỡ nợ. Tác giả sẽ sử dụng mạng nơ ron để phân loại các ngân hàng và so sánh hiệu suất phân loại với mô hình Logit dữ liệu mảng. Lý thuyết về mạng nơron bắt đầu xuất hiện năm 1943 và cho đến năm 1990 nó trở thành một công cụ quan trọng được sử

dụng trong nghiên cứu dự báo vỡ nợ. Mạng nơ ron nhân tạo (ANN) là mô hình tính toán mô phỏng các chức năng mạng sinh học thần kinh, não của con người. Mỗi nơron là một đơn vị xử lý thông tin và là thành phần cơ bản của ANN. Hình 2.1 mô tả cấu trúc của một nơron.

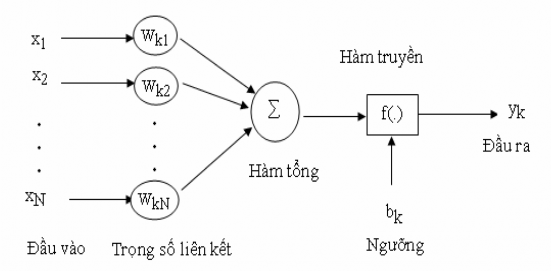
Hình 2.1: Nơron nhân tạo

Các thành phần cơ bản của một nơron bao gồm:

Nguồn: Atlman (1994)

+ Tập các đầu vào: Là các tín hiệu vào của nơron, các tín hiệu này thường được đưa vào dưới dạng một vector N chiều.

+ Tập các liên kết: Mỗi liên kết được thể hiện bởi một véc tơ trọng số (gọi là trọng số liên kết). Trọng số liên kết giữa tín hiệu vào thứ j và nơron k thường được kí hiệu là wkj. Thông thường, các trọng số này được khởi tạo một cách ngẫu nhiên ở thời điểm khởi tạo mạng và được cập nhật liên tục trong quá trình học của mạng.

+ Bộ tổng: Tổng hợp các đầu vào có trọng số liên kết.

+ Ngưỡng (còn gọi là một độ lệch): Ngưỡng này thường được đưa vào như một thành phần của hàm truyền.

+ Hàm truyền: Hàm này được dùng để giới hạn phạm vi đầu ra của mỗi nơron. Nó nhận đầu vào là kết quả của hàm tổng và ngưỡng đã cho. Thông thường, phạm vi đầu ra của mỗi nơron được giới hạn trong đoạn [0,1] hoặc [-1, 1]. Các hàm truyền rất đa dạng, có thể là các hàm tuyến tính hoặc phi tuyến. Việc lựa chọn hàm truyền nào là tuỳ thuộc vào từng bài toán và kinh nghiệm của người thiết kế mạng. Các hàm truyền thường dùng: hàm đồng nhất, hàm bước nhị phân, hàm Log-Sigmoid.

đầu ra.

+ Đầu ra: Là tín hiệu đầu ra của một nơron, với mỗi nơron sẽ có tối đa là một

Xét về mặt toán học, cấu trúc của một nơron k, được mô tả bằng biểu thức sau:

p

yk w ki .xi i1

trong đó: x , x , ..., x : là các tín hiệu vào;

1 2 p

(wk1 , w k 2 ,..., w kp ) là các trọng số

liên kết của nơron thứ k; bk là một ngưỡng; f là hàm truyền và yk là kết quả đầu ra.

Mô hình mạng nơron

Mặc dù mỗi nơron đơn lẻ có thể thực hiện những chức năng xử lý thông tin nhất định, sức mạnh của tính toán nơron chủ yếu có được nhờ sự kết hợp các nơron trong một kiến trúc thống nhất. Một mạng nơron là một mô hình tính toán được xác định qua các tham số: kiểu nơron (như là các nút nếu ta coi cả mạng nơron là một đồ thị), kiến trúc kết nối (sự tổ chức kết nối giữa các nơron) và thuật toán học (thuật toán dùng để học cho mạng).

Về bản chất một mạng nơron có chức năng như là một hàm ánh xạ F: X → Y, trong đó X là không gian trạng thái đầu vào và Y là không gian trạng thái đầu ra của mạng. Các mạng làm nhiệm vụ ánh xạ các vector đầu vào x  X sang các vector đầu ra y  Y thông qua “bộ lọc” các trọng số. Tức là y = F(x) = s (W, x), trong đó W là ma trận trọng số liên kết. Hoạt động của mạng thường là các tính toán số thực trên các ma trận và để thực hiện các nhiệm vụ thì mạng cần được huấn luyện.

Một mạng nơron được huấn luyện sao cho với một tập các vectơ đầu vào X, mạng có khả năng tạo ra tập các vectơ đầu ra mong muốn Y của nó. Tập X được sử dụng cho huấn luyện mạng được gọi là tập huấn luyện. Các phần tử x thuộc X được gọi là các mẫu huấn luyện. Quá trình huấn luyện bản chất là sự thay đổi các trọng số liên kết của mạng. Trong quá trình này, các trọng số của mạng sẽ hội tụ dần tới các giá trị sao cho với mỗi vector đầu vào x từ tập huấn luyện, mạng sẽ cho ra vector đầu ra y như mong muốn. Với nghiên cứu này tập các đầu vào của mạng nơron là các quan sát với các thuộc tính là các biến độc lập, đầu ra là các kết quả phân lớp Y= 1 (nguy cơ vỡ nợ cao); Y = 0 (nguy cơ vỡ nợ thấp).

Có ba phương pháp huấn luyện phổ biến là huấn luyện có giám sát, huấn luyện không giám sát và huấn luyện tăng cường. Trong nhiều nghiên cứu đã chỉ ra mô hình mạng nơron tốt hơn một số mô hình thống kê trong dự báo vỡ nợ (Davalos và cộng sự (1999); Han và Lee (1997); Tsukuda và Baba (1996); Lee và cộng sự (2005)).

Ưu điểm: Mạng nơron không có những hạn chế của các kỹ thuật thống kê truyền thống chẳng hạn như không đòi hỏi điều kiện tuyến tính, phân phối chuẩn. Mạng nơron dễ dàng mô hình các mối quan hệ phức tạp, phi tuyến giữa các đầu vào và các biến đầu ra. Mạng nơron có khả năng chịu lỗi trong dữ liệu, chấp nhận giá trị bị mất, và có thể nhanh chóng thích nghi với các thông tin mới.

Nhược điểm: Không có thủ tục chính thức để xác định cấu trúc liên kết mạng tối ưu cho một vấn đề cụ thể. Cơ cấu nội bộ của mạng nơ ron làm cho nó khó khăn để theo dõi các bước dẫn đến đầu ra, do đó khó để giải thích kết quả cũng như khó đề xuất các kiến nghị chính sách. Ngoài ra mạng nơ ron đòi hỏi thời gian huấn luyện, việc tính toán xác suất vỡ nợ chỉ đến một mức độ giới hạn nhất định và cần những nỗ lực đáng kể.

2.3.3. Cây quyết định

Cây quyết định (DT) được sử dụng nhiều cho vấn đề phân loại và dự báo trên phạm vi thế giới, tuy nhiên ở Việt Nam mô hình này gần như vắng bóng. Tác giả thực nghiệm mô hình DT để phân loại các NHTMCP Việt Nam, so sánh các mô hình để đề xuất mô hình cảnh báo. Cây quyết định là quá trình phân tích dữ liệu, phân lớp. Cây quyết định chia một tập dữ liệu thành các tập dữ liệu con sao cho các tập dữ liệu con này đồng nhất hơn với biến phân lớp. Cây quyết định có cấu trúc biểu diễn dưới dạng cây gồm nút quyết định và nút lá, đỉnh trên cùng của cây gọi là gốc. Mỗi nút quyết định tương ứng với một thử nghiệm trên một thuộc tính duy nhất của dữ liệu đầu vào và mỗi nút quyết định xử lý một kết quả của thử nghiệm. Mỗi nút lá là kết quả của quyết định cho 1 trường hợp. Hình 2.2 mô tả cấu trúc một cây quyết định dạng đơn giản

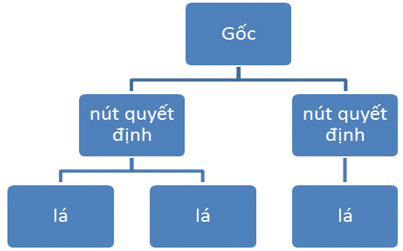
Hình 2.2: Sơ đồ cây quyết định dạng đơn giản