Tuabin thủy lực

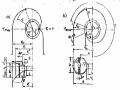
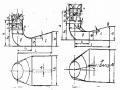
phân loại turbine. Lưu lý rằng khi chế độ làm việc của turbine thay đối, ứng với mỗi trị số cột nước cho trước thì hệ số tỷ tốc cũng thay đổi, bới vậy để so sánh các turbine theo kiểu tỷ tốc chỉ có thể tiến hành trong điều kiện chúng làm việc ở cùng một chế độ. Thường hệ số tỷ tốc được tính ứng với turbine có công suất định mức, cột nước tính toán và số vòng quay đồng bộ.

Từ các công thức tỷ tốc ở trên ta thấy: nếu hai turbine có cùng đường kính BXCT D1 và cùng cột nước H thì turbine nào có tỷ tốc lớn hơn sẽ cho công suất và vòng quay lớn hơn. Do vậy nếu dùng turbine có tỷ tốc lớn ứng với công suất cho trước sẽ cho phép giảm D1 và số vòng quay lớn. Do đó xu thế phát triển của ngành chế tạo turbine là tìm cách tăng tỷ tốc của turbine để giảm nhỏ kích thước turbine và kích thước máy phát.

IV. 3. 4. Tính toán hiệu suất turbine thực từ turbine mô hình

Trong thực tế tuy hai turbine tương tự cùng làm việc ở chế độ tương tự nhưng hiệu suất của chúng vẫn khác nhau. phụ thuộc vào cột nước và đường kính BXCT. Sở dĩ có sự khác nhau nầy vì trong công thức chúng ta tính gần đúng đã bỏ qua các tỷ số hiệu suất, do vậy đã bỏ qua sự khác nhau về tổn thất giữa hai turbine tương tự do tính phức tạp và cũng chưa có cách tính chính xác các tổn thất này.

Trong thực tế xác định hiệu suất của turbine thực thường phải dùng đến các công thức kinh nghiệm và cũng chỉ mới dựa vào chế độ làm việc tối ưu của turbine mô hình . Công thức kinh nghiệm xác định hiệu suât toàn phần của turbine thực như sau :

D1M

D1T

Khi cột nước H  150 m:

Có thể bạn quan tâm!

Xem toàn bộ 317 trang tài liệu này.

max T

1 (1 

max M )

(4-24)

Khi cột nước H > 150 m:

max T

1 (1 

max M )

20 HM

D1M

D1T

(4-25)

Đối với turbine khi thí nghiệm mô hình ta đã xác định được hiệu suất thuỷ lực với mọi trị số cột nước thì có thể xác định hiệu suất turbine thực tơng ứng theo công thức sau:

iT 1 (1 iM

⎡

) ⎢(1 ) 6

⎣

ReM ⎤

⎥

ReT ⎦

(4-26)

Trong (4-26)  là số phần trăm hiệu suất, nó phụ thuộc vào chế độ làm việc của turbine, khó tính ra được, người ta chọn gần đúng  theo điều kiện làm việc tối ưu của turbine là

 = 0,5 và dùng chung cho mọi chế độ làm việc. Còn

ReM D1M .

ReT D1T

Trong tính toán hiệu chỉnh hiệu suất turbine thực từ mô hình người ta thường sử dụng các công thức (4-24) và (4-25) để tính, với độ chính xác gần đúng cho phép.

Chương V. THÍ NGHIỆM MÔ HÌNH VÀ ĐẶC TÍNH TURBINE

V. 1. MÔ HÌNH VẬT LÝ VÀ HỆ THỐNG THÍ NGHIỆM

Hiện nay những phương pháp tính toán lý thuyết vẫn chưa đủ để xác định hình dáng tốt nhất của các bộ phận qua nước của turbine (BXCT, CCHD, vòng bệ, buồng turbine, ống xả ....) ở phần lớn các chế độ làm việc. Đặc biệt khó, hoặc không thể, xác định được các tính chất năng lượng và khí thực cuả turbine ở chế độ làm việc khác với chế độ thiết kế nếu chỉ dựa vào lý thuyết. Vì vậy, để thiết kế các turbine hiện đại thường người ta đưa ra một số phương án phần qua nước và tính toán chúng theo các công thức lý thuyết. Theo kết quả tính toán, chế tạo ra các mô hình của phần qua nước của turbine rồi đem thí nghiệm ở phòng thí nghiệm, từ kết quả thí nghiệm và thông qua luật tương tự tính toán chỉnh lý thành các đường đặc tính mô hình, từ đó xây dựng thành các đường đặc tính khác của turbine thực tế. Việc thí nghiệm cũng có thể tiến hành trực tiếp qua những turbine đang hoạt động ở các TTĐ nhưng tốn kém và không đủ điều kiện bằng trong phòng thí nghiệm.

Việc thí nghiệm tiến hành trong môi trường nước do vậy chủ yếu cần đảm bảo ba điều kiện tương tự và chuẩn số Raynon. Để xác định các đặc tính năng lượng và khí thực của turbine, cần xây dựng những hệ thống thí nghiệm.

Hệ thống thí nghiệm bao gồm những bộ phận chính sau:

- Hai bể chứa nước có dung tích đủ lớn để đóng vai trò bể nước thượng và hạ lưu;

- Turbine mô hình, thường có đường kính BXCT D1M thường 250 và 460 mm;

- Máy bơm để bơm nước từ bể hạ lưu lên bể thượng lưu để lưu thông nước giữa các bể và tạo cột nước cho turbine mô hình;

- Thay thế máy phát điện là một thiết bị đo công suất trên trục turbine mô hình;

- Các thiết bị đo các thông số cần thiết như Q, H, n, ...

Thường có hai loại hệ thống thí nghiệm: hệ thống hở và hệ thống kín.

V. 1. 1. Hệ thống thí nghiệm hở

Hình (5-1,a) trình bày sơ đồ hệ thống thí nghiệm hở. Đặc điểm của nó là có mặt thoáng ở hai bể nước thượng và hạ lưu, mặt thoáng chịu áp suất khí trời. Cột nước của mô hình là hiệu chênh lệch mực nước của hai bể, vì vậy cột nước tạo được là nhỏ. Mô hình hở chỉ có thể thí nghiệm năng lượng mà không thể thí nghiệm khí thực.

Theo sơ đồ thí nghiệm này, khi làm việc nước từ bể thượng lưu 2 chảy qua ống áp lực vào turbine 4 tháo qua ống xả xuống bể hạ lưu 7, ở đây lưu lượng Q được đo bằng đập tràn thành mỏng tam giác vuông 8. Nước qua đập tràn xuống bể dưới và được bơm lên bể 2 nhờ máy bơm 1 và quá trình lại tuần hoàn.

Khi làm thí nghiệm, để tiến hành đo các đại lượng chính như: lưu lượng Q, cột nước H, số vòng quay n, mômen xoắn M, cần dùng những thiết bị và cơ cấu sau:

Lưu lượng Q chảy qua turbine được xác định theo chiều cao lớp nước trên đỉnh đập tràn h (m), biết h có thể xác định lưu lượng theo công thức kinh nghiệm sau:

Q 1,343h 2,47

(l/s)

Để chính xác hơn có thể đo Q bằng phương pháp thể tích, tức là dùng thùng đong.

Đo cột nước H bằng ống đo áp nối riêng ở bể thượng lưu và bể hạ lưu khi mực nước ở hai bể ổn định, hoặc đo theo hiệu số vị trí phao của mực nước ở hai bể.

Đo số vòng quay n (v/ph) trục turbine bằng vòng quay kế kiểu ly tâm hoặc dùng máy đếm vòng quay bằng điện.

Đo mômen xoắn trên trục turbine bằng bộ hãm kiểu ma sát (hình 5-1,b). Mômen xoắn được tính theo công thức: M = P.l, từ M có thể tính ra công suất hữu ích Nh = M.

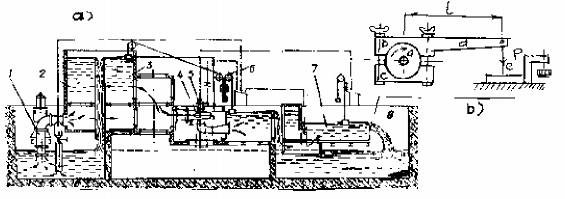
Hình 5-1. Sơ đồ hệ thống thí nghiệm hở.

Nội dung thí nghiệm để xác định đặc tính năng lượng của turbine trên các băng thử gồm: Thí nghiệm với một số độ mở cánh hướng dòng a0 và góc đặt cánh .

- Với mỗi độ mở cánh hướng dòng không đổi a0 = const, và góc đặt cánh không đổi (đối với turbine cánh quay)  = const, ta điều chỉnh van khoá trên đường ống áp lực của turbine. Ứng với mỗi độ mở van khoá ta đo được thông số: cột nước H, số vòng quay n,

lưu lượng Q, công suất hữu ích Nh của turbine.

Tiến hành thay đổi độ mở van khoá theo thứ tự từ lớn đến nhỏ (khoảng chừng 6 - 8

độ mở) và đo các đại lượng H, n, Q, Nh tương ứng với từng độ mở khoá.

- Sau khi có các giá trị H, n, Q, Nh của các điểm ứng với mỗi độ mở khoá, tính hiệu suất và xây dựng các đường cong quan hệ giữa từng cặp thông số với nhau. Từ các đường đặc tính quan hệ xây dựng đặc tính tổng hợp của mô hình.

V. 1. 2. Hệ thống thí nghiệm kín

Đặc điểm của hệ thống thí nghiệm kín là bể thượng và hạ lưu đóng kín không thông với khí trời và cột nước thí nghiệm do máy bơm tạo ra.

Hình (5-2) là một sơ đồ của hệ thống thí nghiệm kín. Hệ thống gồm nguồn tạo áp bơm 1, van khoá 12, nước vào bình cao áp 13, trên ống áp lực đặt thiết bị đo lưu lượng 11, nước vào bình ổn định vận tốc 8, 9 trước khi vào turbine 4, rồi theo ống xả xuống bể kín hạ lưu 2, trở về máy bơm 1, và quá trình lặp lại. Thiết bị để đo các thông số gồm có: đo vòng quay 5, đo công suất 6, các áp kế 14, 15 để đo cột nước .Hệ thống kín ngoài việc tiến hành thí nghiệm năng lượng còn có khả năng thí nghiêm về khí thực

. Do vậy trong hệ thống này có trang bị thêm bơm chân không 3 để hút không khí phía trên mặt nước bình 2.

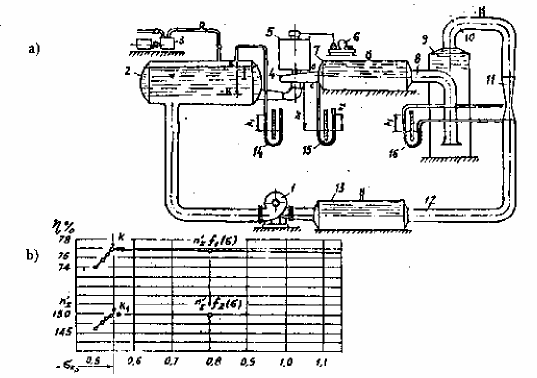
Hệ thống kín có ưu điểm là có khả năng thí nghiệm khí thực, kích thước nhỏ, tuy nhiên hệ thống này có kết cấu phức tạp, thiết bị đo cũng phức tạp hơn hệ thống hở.

Hình 5-2. Sơ đồ hệ thống thí nghiệm tirbine kín

Việc thí nghiệm năng lượng tiến hành với các độ mở a0 = const và các góc đặt của cánh BXCT  = const (đối turbine cánh quay) được tiến hành theo trình tự và nội dung tương tự đã tiến hành đối với hệ thống hở. Ở đây chỉ trình bày cách thí nghiệm khí thực. Nội dung của thí nghiệm khí thực trên hệ thống thí nghiệm kín nhằm vẽ được quan hệ giữa hiệu suất  và hệ số khí thực  ứng với các độ mở a0 (và ) hằng số. Kết quả đo được quan hệ  = f() tính toán và vẽ được các đường đồng hệ số khí thực trên đường đặc tính tổng hợp chính của turbine.

Phương pháp thí nghiệm khí thực được tiến hành trên hệ thống kín. Sau khi đã tiến hành thí nghiệm đặc tính năng lượng thì có thể định ra các chế độ cần thiết phải tiến hành xác định đặc tính khí thực tại các chế độ đó, cụ thể là xác định hệ số khí thực  của các chế độ đó. Ví dụ cần xác định hệ số  ở chế độ A nào đó ( có a0, , HA, QA, nA, NA) ta điều chỉnh khoá 12 trên ống áp lực để có được các thông số HA, QA, nA, NA . Sau đó, cho bơm chân không 3 làm việc , đo áp suất trong bể hạ lưu 2 được giá trị áp suất chân không P2 nào đó ở bể 2. Hệ số khí thực tính được theo công thức:

P 2 

HA

Pbh 

HA

(5-1)

Trong (5-1): Pbh là áp suất hoá hơi ứng với nhiệt độ nước thí nghiệm; HS - chiều cao hút của turbine thí nghiệm.

Tương ứng với trạng thái A ta cũng tính được A theo công thức chung:

Nh 102. M.100%

(5-2)

N .Q. H

trong công thức (5-1): M = P.l (kGm);  = 1000 kG/m3, Q (m3/s), H (m cột nước).

Như vậy ứng với mỗi giá trị của áp suất chân không P2 do máy bơm chân không tạo ra và nhiệt độ của nước, ta có được một trị số  tính theo công thức (5-1) và  theo công thức (5-2). Giữ nguyên chế độ A, thay đổi chân không P2 bằng cách thay đổi chế độ làm việc của máy bơm chân không 3, ta có một loạt các cặp quan hệ giữa  và . lập quan hệ  = f() ứng với a0.

Hiện tượng khí thực sẽ xảy ra khi lưu lượng, cột nứơc và áp suất giảm mạnh, kéo theo sự rung động máy và tiếng ồn. Trên thiết bị đo ta có thẻ xác định được các giá trị này. Căn cứ vào đồ thị (hình 5-2,b) để xác định hệ số khí thực tới hạn KP (điểm k) ở chế độ A. Thay đổi chế độ khác, theo các quy trình trên lặp lại. Thí nghiệm khí thực đòi hỏi mât nhiều công sức và kinh nghiệm mới bảo đảm chính xác.

V. 2. ĐƯỜNG ĐẶC TÍNH CỦA TURBINE

Đường biểu thị quan hệ giữa các thông số của turbine gọi là đường đặc tính của turbine. Có hai loại đường đặc tính: đặc tính đơn và đặc tinh tổng hợp. Các đường đặc tính đơn biểu thị quan hệ giữa các cặp hai thông số một; các đường đặc tính tổng hợp biểu thị quan hệ giữa nhiều thông số của turbine.

V. 2. 1. Đường đặc tính đơn

Từ kết quả thí nghiệm, sau khi xác định được c thông số ở các chế độ khác nhau ta có thể thiết lập quan hệ giữa các cặp thông số, còn các thông số khác là hằng số. Có ba loại đường đặc tính đơn: đặc tính công tác, đặc tính vòng quay, đặc tính cột nước.

1. Đường đặc tính công tác

Các đường đặc tính công tác nàu biểu thị các quan hệ: , Q, a0 = f(N), hoặc các quan hệ N, , a0 = f(Q), hoặc quan hệ Q, , N = f(a0), trong điều kiện: n = const và cột nước H = const (hình 5-3). Các quan hệ này biểu thị các thông số ở dạng không thứ nguyên tính theo phần trăm.

Qua các đường trên cho phép ta có những nhận xét cần thiết đối với turbine:

- Trên đường đặc tính công tác công suất (hình a): khi  = 0 và N = 0 thì Q và a0 vẫn khác không, vì rằng muốn phát ra được một công suất hửu ích nào đó thì cần phải có một lưu lượng không tải tương ứng với độ mở nhỏ nhất nào đó đê khắc phục các tổn thất nhất định trong turbine. Mặt khác ta thấy hiệu suất lớn nhất không ứng với công suất lớn nhất, mà ứng với một giá trị công suất nhỏ hơn công suất lớn nhất.

- Trên hai đường đặc tính lưu lượng và độ mở (hình b,c) ta thấy hiệu suất và công suất hữu ích bằng không ứng với Q và a0 luôn nhỏ hơn 100%.

Trong các đường đặc tính công tác người ta hay dùng dạng riêng biểu thị quan

hệ

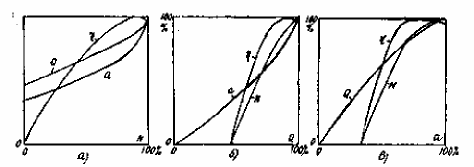
Hình 5-3. Các đường đặc tính công tác cuả turbine

giữa hiệu suất và công suất của các loại turbine khác nhau ( hình 5-4), nhằm so sánh đặc tính hiệu suất giữa các turbine. Qua đường này ta có nhận xét:

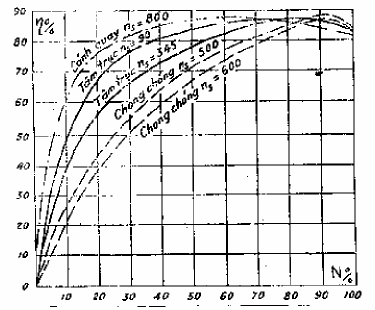
Hình 5-4. Đường đặc tính công tác của các loại turbine

- Turbine gáo có hiệu suất max nhỏ nhất, nhưng đường đặc tính thoải nên có vùng làm việc với hiệu suât cao được nới rộng;

- Hiệu suất max cuả turbine tâm trục và turbine cánh quạt lớn nhất trong các loại turbine. Tuy vậy nhưng đường này của turbine tâm trục tương đối dốc nên vùng làm việc có hiệu suất cao bị giảm, còn đường của turbine cánh quạt thì rất dốc nên vùng làm việc với hiệu suất cao bị thu hẹp nhiều;

- Turbine cánh quay có đường đặc tính công tác thoải hiệu suất cao lớn, do vậy có vùng làm việc với hiệu suát cao mở rộng hơn cả. Sở dĩ có được tính ưu việt này là nhờ cánh xoay được để đưa trạng thái làm việc về gần trạng thái thiết kế.

2. Đường đặc tính vòng quay

Đường đặc tính vòng quay biểu thị các thông số Q, N,  theo vòng quay n khi đường kính D1, H, a0 không đổi (hình 5-5,a). Từ đường này ta thấy hiệu suất cao không trùng với N và Q lớn nhất. Khi n tăng thì các thông số sẽ thay đổi.

l/s

Hình 5-5. Các đường đặc tính vòng quay và đặc tính cột nước.

3. Đường đặc tính cột nước

Đường đặc tính này biểu thị quan hệ giữa các thong số Q, N,  của turbine theo cột nước H. Cột nước của turbine luôn thay đổi trong quá trình vận hành. Trên đồ thị ta thấy: ứng với  = 0 và N = 0 thì cần có cột áp nào đó đặc trưng cho tổn thất thuỷ lực ở chế độ không tải. Nhìn chung khi H tăng thì công suất turbine tăng, nhưng hiệu suất cao nhất lại đạt được ở một giá trị cột nước nào đó ứng với độ mở a0 khác nhau. Còn lưu lượng Q thì tăng cùng với H tăng (hình 5-5,b).

V. 2. 2. Đường đặc tính tổng hợp

Các đường đặc tính đơn đã nghiên cứu ở trên chỉ mới biểu thị được quan hệ giữa từng cặp thông số trong khi những thông số coi như không thay đổi, điều này khác với thực tế vận hành của turbine là các thông số đồng thời tham gia vận hành và thay đổi. Vì vậy cần có đường đặc tính biểu thị các thông cùng tham gia vận hành. Đường đặc tính như vậy gọi là đường đặc tính tổng hợp. Có hai loại đường đặc tónh tổng hợp là: Đường đặc tính tổng hợp chính và Đường đặc tính tổng hợp vận hành.

1. Đường đặc tính tổng hợp chính

Đường đặc tính tổng hợp chính được lập ra từ thí nghiệm mô hình của một turbine mẫu đại diện cho một kiểu turbine, từ kết quả thí nghiệm mô hình , sử dụng các công thức tương tự và quy dẫn tính toán vẽ ra cho một turbine có đường kính D1 = 1m, làm việc với cột nước H = 1m. Do vậy đường này dùng cho mọi turbine có kích thước khác nhau nhưng cùng một kiểu .Đường đặc tính tổng hợp chủ yếu biểu diễn các

thông số turbine thông qua hai biến là vòng quay quy dẫn n1’ và lưu lượng quy dẫn Q1’, nó gồm các họ đường sau (hình 5-6):

Hình 5-6. Các đường đặc tính tổng hợp chính

- Họ các đường đồng hiệu suất = f (n1’, Q1’) ;

- Họ các đường đồng độ mở cánh hướng dòng a0 = f (n1’, Q1’) ;

- Họ các đường đồng hệ số khí thực  = f (n1’, Q1’) ;

- Đường hạn chế 5% công suất (chỉ có ở turbine tâm trục và cánh quạt, hình 5-6,a) ;

- Họ các đường đồng góc đặt cánh  = f (n1’, Q1’) dùng đối với turbine cánh quay (xem hình 5-6,c).

- Từ đường đặc tính của TB gáo (hình 5-6,b), ta thấy các đường đồng độ mở a0 được thay thế bởi các đường đồng hành trình van kim trong vòi phun s = f (n1’, Q1’) .

Các đường đồng hiệu suất của turbine cánh quạt rất dốc, nghĩa là vùng làm việc với hiệu suất cao rất hẹp. Ngược lại, ở turbine cánh quay và turbine gáo thì các đường đồng hiệu suất thoãi, do vậy vùng làm việc với hiệu suất cao của những loại turbine này