Trong Nghiên Cứu Của Dave Và Cộng Sự (2010), Tác Giả Đã Mở Rộng Thí Nghiệm

BART (Balloon Analogue Risk Task): Phương pháp này đo lường sở thích rủi ro bằng cách thực hiện mô phỏng trên máy tính việc bơm không khí vào các quả bóng bay (Lejuez và cộng sự, 2002). Các quả bóng bay có 3 màu sắc khác nhau (xanh, vàng và da cam) và được đưa ra cùng một lúc. Sau mỗi lượt bơm, quả bóng sẽ lớn dần và mỗi cá nhân cũng sẽ kiếm được số tiền tích lũy (tạm thời) tương ứng theo kích thước quả bóng. Số tiền tích lũy này sẽ không cho những người tham gia biết. Khi quả bóng ngày càng lớn, khả năng nó bị nổ sẽ ngày càng tăng nếu vẫn tiếp tục bơm thêm. Ban đầu, xác suất quả bóng bị nổ không đáng kể trước lần bơm đầu tiên, nhưng xác suất này sẽ tăng lên cho đến một giá trị chắc chắn khi quả bóng ở một kích thước nhất định. Nếu quả bóng bị nổ, tất cả số tiền tích lũy tạm thời trước đó sẽ biến mất và một quả bóng mới sẽ được giao cho người chơi. Tại mỗi thời điểm, người tham gia có thể lựa chọn hoặc là bơm bóng tiếp hoặc là dừng lại và nhận số tiền mà người đó đã kiếm được trước đó. Nếu dừng lại và ghi nhận số tiền của mình, số tiền đó sẽ được giữ cố định trong tài khoản của người tham gia, đồng thời người tham gia sẽ tiếp tục bơm với một quả bóng mới. Mỗi người tham gia sẽ thực hiện với lần lượt 90 quả bóng bay. Sau 90 lần thực hiện, trung bình số lần mà các quả bóng bay được bơm không bị nổ sẽ được xem là giá trị điều chỉnh tương ứng với sự ưa thích rủi ro của mỗi cá nhân. Xác suất bóng nổ sẽ tăng tuyến tính với mỗi lần bơm bóng theo một hàm số cụ thể, tương ứng với màu sắc của quả bóng đó. Với các quả bóng màu xanh, xác suất bóng nổ là 1/128 sau lần bơm đầu tiên, 1/127 sau lần thứ hai, 1/126 sau lần thứ ba và tiếp tục giảm tương ứng sau mỗi lần bơm. Sau 128 lần bơm, quả bóng chắc chắn sẽ bị nổ. Số lần bơm mà các quả bóng màu cam và màu vàng chắc chắn bị nổ lần lượt là 8 và 32 lần bơm. Những người tham gia sẽ được biết thông tin này sau khi thực hiện xong thí nghiệm, nhưng xác suất thực tế của mỗi quả bóng bị nổ sẽ không được tiết lộ trước khi tham gia trò chơi.

Phương pháp này đã được thực hiện trong một số nghiên cứu về khoa học thần kinh, đối với người nghiện ma túy và bệnh tâm thần (Hunt và cộng sự, 2005). Tuy nhiên, vẫn còn một số tranh luận về giá trị điều chỉnh tương ứng rủi ro của các cá nhân. Theo Lejuez và cộng sự (2002), giá trị điều chỉnh sẽ phản ánh rủi ro của các

cá nhân có tương quan cao với việc ưa thích rủi ro trong đời sống hàng ngày của các học sinh trung học.

Gợi mở thông qua việc sử dụng bảng câu hỏi.

Phương pháp này gợi mở sở thích rủi ro dựa trên câu trả lời của những người tham gia về một câu hỏi có tính rủi ro. Từ đó sẽ cho thấy xu hướng đối với rủi ro của họ. Các câu hỏi phổ biến theo phương pháp này thường là “Mức độ sẵn lòng chấp nhận rủi ro của bạn là bao nhiêu?” cho một vấn đề nào đó. Người tham gia sẽ đánh giá bằng cách cho điểm theo thang đo 10 điểm, với 1 là hoàn toàn không sẵn lòng và 10 là hoàn toàn sẵn lòng.

Các nghiên cứu theo phương pháp này cho thấy, sở thích rủi ro sẽ phụ thuộc đáng kể vào lĩnh vực được gợi mở, chẳng hạn, Weber và cộng sự (2002) đã thực hiện nghiên cứu theo phương pháp này với 40 ngành khác nhau: 8 ngành trong các lĩnh vực rủi ro giải trí, sức khỏe, xã hội và đạo đức; 4 ngành trong lĩnh vực cờ bạc và đầu tư. Trong nghiên cứu, các tác giả yêu cầu những người tham gia cho điểm theo thang điểm 5 – tương ứng với việc sẵn lòng tham gia của họ – với các câu hỏi như “uống nhiều rượu tại một hoạt động xã hội” hay “bỏ 1 tuần thu nhập ra chơi cờ bạc tại 1 casino”… Tuy nhiên, do các bảng câu hỏi gợi mở rủi ro một cách gián tiếp nên các nhà nghiên cứu đã đưa ra nhiều tranh luận về phương pháp này. Holt và Laury (2002) đã đưa ra một số nghi vấn về phương pháp này như sau: Liệu phương pháp này có phản ánh chính xác thái độ của các cá nhân với sở thích rủi ro, nhất là trong các quyết định về tài chính hay không? Liệu trong thực tế, các câu hỏi này có phản ánh chính xác thái độ hướng đến rủi ro của những người tham gia không khi họ sẽ phải đối mặt với sự mất mát?

Phương pháp của Gneezy và Potters.

Có thể bạn quan tâm!

Xem toàn bộ 221 trang tài liệu này.

Phương pháp này được Gneezy and Potters (1997) đưa ra để đo lường sở thích rủi ro trong các quyết định tài chính với số tiền chi trả thực tế. Người tham gia sẽ nhận được X USD và được yêu cầu sử dụng một số tiền x USD trong đó để đầu tư

vào một lựa chọn rủi ro. Lượng tiền được đầu tư có thể tạo ra mức thu nhập từ cổ tức. Tổng số tiền nhận được việc đầu tư là kx USD (k > 1) với xác suất p và xác suất bị thua lỗ là (1 – p). Số tiền không được đầu tư còn lại là (X – x) USD được nhà đầu tư nắm giữ. Khi đó, tổng số tiền của nhà đầu tư có thể có là (X – x + kx) USD với xác suất p, hoặc (X – x) USD với xác suất (1 – p). Trong mọi trường hợp, p và k được lựa chọn sao cho p × k > 1, tức là kỳ vọng của việc đầu tư sẽ mang lại giá trị cao hơn so với khi không đầu tư. Vì thế, một người trung lập với rủi ro hoặc tìm kiếm rủi ro có thể sẽ đầu tư toàn bộ số tiền X USD, trong khi một người e ngại rủi ro có thể sẽ đầu tư ít hơn. Những người tham gia sẽ phải quyết định việc lựa chọn x USD để đầu tư. Đây chính là giá trị để đo lường mức độ ưa thích rủi ro của người tham gia.

Phương pháp này đã được sử dụng trong nghiên cứu về các quyết định tài chính của sinh viên (Gneezy và Potters, 1997); của các nhà đầu tư chuyên nghiệp (Haigh và List, 2005); và so sánh sự khác biệt về giới tính trong thái độ với rủi ro (Charness và Gneezy, 2012). Tuy nhiên, Charness và cộng sự (2013) thấy rằng nhược điểm của phương pháp này là không thể phân biệt được người tìm kiếm rủi ro và người trung lập với rủi ro vì những người trung lập và tìm kiếm rủi ro đều có thể sẽ đầu tư toàn bộ số tiền họ nhận được.

Phương pháp của Eckel và Grossman.

Thí nghiệm của Eckel và Grossman (2002) yêu cầu những người tham gia chỉ thực hiện 1 lựa chọn cho 1 trò chơi sau khi đã được nghe giới thiệu về tất cả các trò chơi. Các trò chơi có mức độ rủi ro khác nhau. Theo phương pháp này, Dave và cộng sự (2010) đã đưa ra 6 trò chơi. Trong mỗi lựa chọn trò chơi được liệt kê trong Hình 3.1, họ sẽ có 50% cơ hội chiến thắng và 50% thua cuộc. Những người tham gia sẽ nhận được một thông tin chắc chắn như sau: Với trò chơi 1, họ chắc chắn

nhận được khoản tiền 28 USD. Đối với trò chơi từ 1-5, số tiền nhận được kỳ vọng của người chơi sẽ gia tăng tuyến tính với mức độ rủi ro (đại diện là độ lệch chuẩn). Trò chơi thứ 6 có cùng số tiền kỳ vọng như trò chơi 5 nhưng có độ lệch chuẩn cao hơn. Những trò chơi này sẽ được thiết kế sao cho những người không ưa thích rủi ro nên lựa chọn những trò chơi có độ lệch chuẩn thấp hơn (trò chơi từ 1-4), những người trung lập với rủi ro nên chọn trò chơi có lợi nhuận kỳ vọng cao hơn (trò chơi 5), và những người tìm kiếm rủi ro nên chọn trò chơi số 6.1

Hình 3.1: Các lựa chọn trò chơi của Eckel và Grossman.

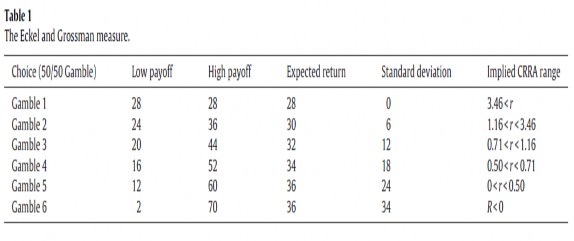
(Nguồn: Charness và cộng sự, 2013).

Phương pháp này sẽ ước lượng các tham số của các trò chơi nhằm phản ánh khoảng cách rủi ro với giả định hệ số không ưa thích rủi ro là hằng số (Constant Relative Risk Aversion – CRRA), đại diện là r. Mỗi khoảng giá trị r được tính toán bằng cách tạo ra mức độ hữu dụng tương ứng trong việc đánh đổi giữa các trò chơi liền kề.Tính hữu dụng sẽ được thể hiện thông qua hàm số u (x) = x1 – r, với r là hệ số e ngại rủi ro và x là giá trị của tài sản. Các cá nhân với r > 0 được phân loại là e ngại rủi ro, r < 0 là ưa thích rủi ro và r = 0 là trung lập với rủi ro. Hình 3.1 cho thấy khoảng cách của các hệ số rủi ro tương ứng với các trò chơi. Khoảng cách giữa các hệ số được xác định bằng cách tính toán giá trị của r sao cho các giá trị sẽ tạo ra sự

1 Trong nghiên cứu của Dave và cộng sự (2010), tác giả đã mở rộng thí nghiệm với việc so sánh về địa điểm thực hiện thí nghiệm: Ở lớp học, ở hội nghị trong khách sạn, phòng họp của Ban Giám đốc…

trung lập giữa việc chọn trò chơi này và 2 trò chơi liền kề. Ví dụ, một sự lựa chọn của Gamble 3 hàm ý rằng có một hệ số rủi ro nằm trong khoảng (0,71; 1,16): Sự trung lập giữa trò chơi 3 và 4 tương ứng với r = 0,71 và sự trung lập giữa trò chơi 2 và 3 là r = 1,16.

Eckel và Grossman (2008) thấy rằng nữ giới có mức độ e ngại rủi ro đáng kể hơn nam giới. Đồng thời, các tác giả cũng thấy rằng cả nam và nữ giới đều dự đoán nữ giới thường e ngại rủi ro hơn. Theo Dave và cộng sự (2010), phương pháp này ước tính sở thích rủi ro đơn giản và dễ thực hiện hơn các phương pháp gợi mở phức tạp khác, nhất là khi khả năng và trình độ tính toán của người tham gia là bị hạn chế. Tuy nhiên, họ cũng thấy rằng phương pháp này không đánh giá được sự khác biệt về mức độ của hành vi tìm kiếm rủi ro.

Phương pháp lựa chọn theo danh sách giá.

Phương pháp này gợi mở sở thích rủi ro dựa trên tương quan giữa đặc điểm của cá nhân với hành vi chấp nhận rủi ro trong thực tế. Phương pháp này đưa cho người tham gia một chuỗi lựa chọn giữa các trò chơi. Giả định về một dạng hàm chung đối với những người tham gia và đầy đủ dữ liệu từ các lựa chọn, phương pháp này có thể ước lượng các hệ số của hàm hữu dụng.

Hình 3.2: Các lựa chọn trò chơi của Holt và Laury.

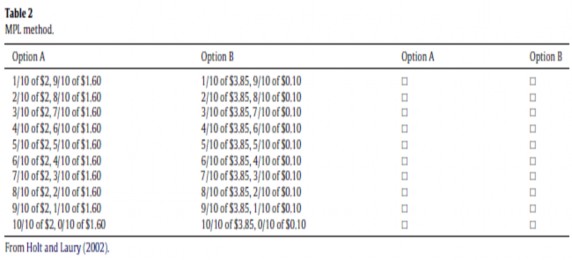
(Nguồn: Holt and Laury, 2002).

Người tham gia sẽ được cung cấp 1 danh sách gồm 10 lựa chọn trong 2 nhóm trò chơi (tương ứng 2 cột A và B) như hình 3.2. Người tham gia được yêu cầu lựa chọn 1 trò chơi mà người đó thích chơi ở mỗi dòng (cột A hoặc B). Số tiền nhận được từ những lựa chọn trong cột A và B là giống nhau ở mỗi dòng (chỉ có khác biệt giữa các dòng lựa chọn). Ví dụ khi lựa chọn hàng đầu tiên, lựa chọn B chỉ có 1/10 cơ hội nhận được khoản tiền cao hơn lựa chọn A, đồng thời số tiền kỳ vọng của lựa chọn A cao hơn 1,17 USD so với lựa chọn B. Vì vậy, chỉ những cá nhân tìm kiếm rủi ro mới lựa chọn cột B ở dòng đầu tiên. Các dòng tiếp theo được thực hiện tương tự như vậy và sau khi các cá nhân thực hiện xong, chúng ta sẽ ước lượng hệ số r. Nếu 4 lựa chọn đầu tiên ở cột A, 6 lựa chọn sau ở cột B thì người đó trung lập với rủi ro với hệ số r nằm trong khoảng (-0,15; 0,15). Nếu 6 lựa chọn đầu là A, 4 lựa chọn sau là B thì người đó không ưa thích rủi ro với hệ số r nằm trong khoảng (0,41; 0,68).1 (Hình 3.3)

Cách tính toán hàm hữu dụng theo CRRA (Hằng số e ngại rủi ro tương đối- Constant Relative Risk Aversion): Các đối tượng sẽ đối mặt với các lựa chọn nhị phân, với giả định số tiền nhận được là M, sự hữu dụng với số tiền nhận được là

1 Lưu ý, cần thông báo cho những người tham gia rằng họ sẽ được chọn ngẫu nhiên 1 canh bạc thực tế để chơi sau thí nghiệm và họ sẽ được trả tiền theo kết quả của canh bạc đó. Bởi vì, nếu 1 người cho rằng những lựa chọn của họ không bị tác động bởi việc trả tiền thì nó sẽ thúc đẩy họ có các lựa chọn rủi ro hơn .

U(M|r) (r là hệ số liên quan đến việc e ngại rủi ro). Với mỗi lựa chọn giữa các canh bạc, hàm hữu dụng kỳ vọng được tính toán như sau:

∑[ ( )]

Với mỗi lựa chọn là i, xác suất xảy ra với số tiềnlà. Hàm hữu dụng U(M|r) được tính toán theo phương pháp CRRA.

Tanaka và cộng sự (2010) thực hiện thí nghiệm theo phương pháp này ở một số vùng nông thôn Việt Nam. Tuy nhiên, điểm hạn chế của phương pháp này là nó sẽ phụ thuộc vào trình độ của người tham gia. Khả năng, trình độ của đối tượng tham gia trong việc hiểu và đưa ra những tính toán giữa các mức rủi ro tương đương sẽ ảnh hưởng đáng kể đến khả năng dự đoán thu nhập của họ. Do đó, khả năng tính toán sẽ là một nhân tố tiềm tàng trong việc đo lường thái độ với rủi ro của người tham gia. Ngoài ra, mức độ giàu có của dân số cũng có thể sẽ tác động đến hành vi của họ.

Hình 3.3: Phân loại e ngại rủi ro dựa trên lựa chọn.

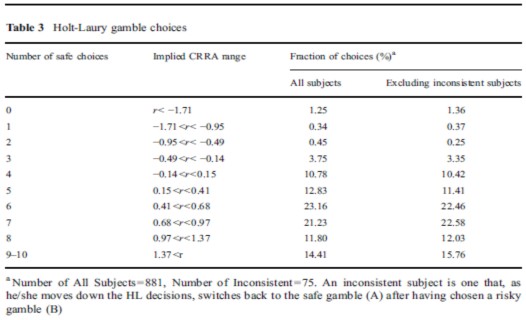
(Nguồn: Holt and Laury, 2002).

3.2.2. Các phương pháp đo lường vốn xã hội.

Theo Nguyễn Tuấn Anh (2011) thì những nghiên cứu về thực nghiệm và ứng dụng về vốn xã hội ở Việt Nam vẫn còn dừng ở giai đoạn khởi động bao gồm nghiên cứu về vốn xã hội của một số doanh nghiệp ở đô thị và một số làng xã ở khu vực nông thôn. Để đo lường vốn xã hội các nhà nghiên cứu sử dụng nhiều phương pháp khác nhau tùy theo mục đích nghiên cứu của mỗi người. Bao gồm khảo sát điều tra xã hội học (GSS), bảng câu hỏi, khảo sát thái độ, phương pháp bỏ phiếu, xổ số, thí nghiệm trực tiếp, thí nghiệm trong phòng thí nghiệm, thông qua Internet…

Đối với thí nghiệm để đo lường về vốn xã hội thì thường được nghiên cứu, xem xét ở hai khía cạnh là cá nhân và theo nhóm (Putnam,1995; Glaeser và cộng sự, 2000). Karlan (2005) định nghĩa vốn xã hội của cá nhân là khả năng nắm bắt thông tin, sự giao tiếp và các mối quan hệ xã hội của cá nhân đó giúp cho họ nắm rõ để giải quyết và khắc phục các vấn đề có liên quan đến những thông tin không hoàn hảo trong xã hội của cá nhân đó. Sự tin tưởng và niềm tin là hai thành tố quan trọng nằm bên trong vốn xã hội cá nhân.

Dựa trên các câu hỏi khảo sát của GSS với 3 câu hỏi về "niềm tin" (trust), "sự công bằng" (fairness), và "sự giúp đỡ" (helping) để đo lường vốn xã hội, Karlan (2005) đã thiết kế ra 2 trò chơi nhằm đo lường niềm tin và sự tin cậy của các cá nhân.

Trust Game (Trò chơi tin tưởng).

Johnson và Mislin (2001) phân tích hồi quy về sự tin cậy với dữ liệu từ 162 bản sao của trò chơi Berg, Dickhaut và McCabe (1995) (trò chơi tin tưởng) liên quan đến hơn 23.000 người tham gia. Kết quả cho thấy rằng các đối tượng sinh viên gửi lại ít tiền hơn đối tượng không phải học sinh; những người trẻ tuổi cho ít hơn và ít hào phóng hơn những người lớn tuổi. Thử nghiệm với biến địa lý phát hiện cho thấy số tiền được gửi trong trò chơi bị ảnh hưởng đáng kể bởi yếu tố địa lý: Châu Phi gửi ít hơn so với những người ở Bắc Mỹ, người Châu Á gửi nhiều hơn người Bắc Mỹ (số liệu gồm 162 quan sát của 35 quốc gia: 47 nghiên cứu từ Bắc Mỹ, 64 nghiên