Trang chủ / Tài liệu miễn phí / Tập Bài Giảng

Ngôn ngữ hình thức - 22



- G không là văn phạm loại 1 vì luật sinh C vi phạm điều kiện của văn phạm loại 1.

Vậy G là văn phạm loại 0 (văn phạm ngữ cấu). 1b) G = (N, T, P, S); trong đó:

N = {S, A, B, C, D} ; T = {a, b};

P ={S ABC; AB aADb; Dab bDb; DbC BaC; aB Ba; AB ; C };

S = S.

2a) - G không là văn phạm loại 3 vì luật sinh DF B vi phạm điều kiện của văn phạm loại 3;

- G không là văn phạm loại 2 vì luật sinh DF B vi phạm điều kiện của văn phạm loại 2;

- G không là văn phạm loại 1 vì luật sinh DF B vi phạm điều kiện của văn phạm loại 1.

Vậy G là văn phạm loại 0 (văn phạm ngữ cấu).

2b) G = (N, T, P, S); trong đó:

N = {S, A, B, C, D, E, F} ; T = {a, b};

P = {S ABaDF; BD DCB; BC bB; AD AAE; EC AE; EB BE; EF BBDF; DF B | };

S = S.

3a) - G không là văn phạm loại 3 vì luật sinh S SS vi phạm điều kiện của văn phạm loại 3;

- G là văn phạm loại 2 (văn phạm phi ngữ cảnh) vì tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm loại 2.

3b) G = (N, T, P, S) với: N = {S};

T = {a, b};

P = {S SS; S aSb; S bSa; S ab; S ba}.


S = S.

4a) G là văn phạm loại 3 (văn phạm chính quy) vì tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm tuyến tính phải.

4b) G = (N, T, P, S) với: N = {S};

T = {a};

P = {S aS; S a; A abB | B| }; S = S.

1.18. 1) - G là văn phạm loại 3 (văn phạm tuyến tính trái) vì tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm tuyến tính trái.

- G = (N, T, P, S) với:

N = {S, A};

T = {a, b};

P = {S Sab; S Aa; A Sa; A Abbba; A a; S}; S = S.

2) - G là văn phạm loại 1 (văn phạm cảm ngữ cảnh) vì:

+ G không là văn phạm loại 3 vì luật sinh AB BA vi phạm điều kiện của văn phạm loại 3;

+ G không là văn phạm loại 2 vì luật sinh AB BA vi phạm điều kiện của văn phạm loại 2;

+ Tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm loại 1.

- G = (N, T, P, S) với:

N = {S, A, B};

T = {a, b};

P = {S AB; AB BA; A aA; B Bb; A a; B b}; S = S.

3) - G là văn phạm loại 1 (văn phạm cảm ngữ cảnh) vì:

+ G không là văn phạm loại 3 vì luật sinh BbAbb vi phạm điều kiện của văn phạm loại 3;



+ G không là văn phạm loại 2 vì luật sinh BbAbb vi phạm điều kiện của văn phạm loại 2;

+ Tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm loại 1.

- G = (N, T, P, S) với:

N = {S, A, B};

T = {a, b};

P = {S A; S AAB; Aa Aba; A aa; BbAbb; AB

ABB; B b};


S = S.

1.19. 1) - G là văn phạm loại 3 (văn phạm tuyến tính trái) vì tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm tuyến tính trái.

- G = (N, T, P, S) với:

N = {S};

T = {a};

P = {S Sa; S a; S}; S = S.

2) - w = .

Áp dụng luật sinh S, ta có dẫn xuất một bước S .

- w = a.

Áp dụng luật sinh S a, ta có dẫn xuất một bước S a.

Hoặc

Áp dụng luật sinh SSa, rồi áp dụng luật sinh S, ta có dẫn xuất hai bước S

Sa a.

- w = aa.

S Sa Saa aa hoặc S Sa aa.

- w = ai ; với iN.

Áp dụng i-1 lần luật sinh S Sa và một lần luật sinh S a, ta có S i ai. Hoặc áp dụng i lần luật sinh S Sa và một lần luật sinh S , ta có S i+1 ai.

3) L(G) = {ai iN}.


1.20. 1) - G là văn phạm loại 3 (văn phạm tuyến tính phải) vì tất cả các luật sinh của nó đều thỏa mãn điều kiện của văn phạm tuyến tính phải.

- G = (N, T, P, S) với:

N = {S, A, B};

T = {a, b};

P = {S aA; A aA; A aB; B bB; Bb}; S = S.

2) - w = aab.

S aA aaB aab.

- w = aaaaabb.

S aA aaA aaaA aaaaA aaaaaB aaaaabB aaaaabb.

- w = ai bj; với i, jN+; i 2.

Áp dụng 1 lần luật sinh S aA

Áp dụng i-2 lần luật sinh A aA và một lần luật sinh A aB, ta có S i aiB. Áp dụng j-1 lần luật sinh B bB và một lần luật sinh B b, ta có S i+j ai bj.

3) L(G) = {ai bj; với i, jN+; i 2}.

1.21. 1) - G là văn phạm loại 2.

- G = (N, T, P, S) với:

N = {S};

T = {a, b};

P = {S bSa; S}; S = S.

2) - w = .

S .

- w = ba.

S bSa ba.

- w = bi ai; với iN.

Áp dụng i-1 lần luật sinh S bSa và một lần luật sinh S , ta có S i biai.

3) L(G) = {bi ai; với iN}.



1.22. 1) - G là văn phạm loại 2.

- G = (N, T, P, S) với:

N = {S, A};

T = {a, b};

P = {S aAb; S; A aAb; A}; S = S.

2) - w = .

S .

- w = ab.

S aSb ab.

- w = aaaabbbb.

S aAb aaAbb aaaAbbb aaaaAbbbb aaaabbbb.

- w = bi ai; với iN.

Áp dụng 1 lần luật sinh S , ta có S . Áp dụng 1 lần luật sinh S aAb

Áp dụng i -1 lần luật sinh A aAb và một lần luật sinh A , ta có S i+1

aibi với iN+.

3) L(G) = {ai bi ; với iN}.

1.23. 1) - G là văn phạm loại 2.

- G = (N, T, P, S) với:

N = {S, A, B};

T = {a, b};

P = {S AB; A aA; A a; B aB; Bb}; S = S.

2) - w = aab.

S AB aAB aaB aab.

- w = aaaaab.

S AB aAB aaAB aaaAB aaaaB aaaaaB aaaaab.

- w = ai b; với iN+.


Áp dụng 1 lần luật sinh S AB

Áp dụng i-1 lần luật sinh A aA và một lần luật sinh B aB, ta có S i+1 aib. Áp dụng 1 lần B b, ta có S i+2 ai b.

3) L(G) = {ai b; với iN+}.

1.24. 1) S aA; A aA|b|c.

2) S Aab; A aA|b|c.

3) S Aba; A aA|b|c.

4) S Abcd; A aA|b|c. 1.25. 1) S A1; A A0|0.

2) S 0A; A 0A|1.

3) S 0A1; A 0A|0.

Hoặc S AB; A 0A|0; B 1

1.26. 1) S A1; A A1|B; B C000; C .

2) S 000A; A 1A|1.

3) S 000AB; A 1A|1; B .

Hoặc S AB; A 000; B 1B|1.

1.27. S AB; A 0A1|01; B 2B3|.

1.28. SAB; A aAb| ab; B cB|.

1.29. 1) SabA; A abA| B; BcB|c;

2) S Ac; AAc| B; BBab| ab;

3) SabAB; A abA| ; B cB|c. Hoặc SAB; A abA|ab; B cB|c.

1.30. 1) S A2; A A2|B; B B1|C; C 000.

2) S 000A; A 1A| B; B 2B| 2.

3) S 000AB; A 1A|1; B 2B|2.

1.31. 1) S S2| A; A A1|C; C C0|.

2) S 0S|A; A 1A|B; B 2B|.

3) S ABC; A 0A|; B 1B|; C 2C|.

1.32. 1) S S3|A; A A2|B; B B1|C; C C0|.


2) S 0S|A; A 1A|B; B 2B|C;C 3C|.

3) S ABCD; A 0A|; B 1B|; C 2C|; D 1D|.

2. Bài tập chương 2

2.16. 1) Biểu diễn M

a) Dạng bảng:

- q0 = A ;

- F = C, E;

- :


Q

a

b

A

A

B

B

D

E

C

E

D

D

C

E

E

E


Có thể bạn quan tâm!

Xem toàn bộ 254 trang tài liệu này.

Ngôn ngữ hình thức - 22


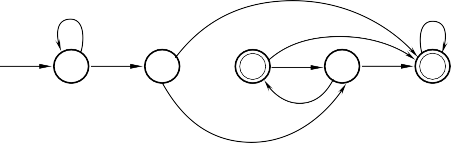
b Dạng đồ thị a a b a Start A b B C b D b E a a 2 Automat M là Automat hữu hạn đơn 1

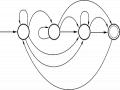
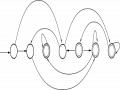
b) Dạng đồ thị: a a

b a

Start A b B

C b D b E a

a

2) Automat M là Automat hữu hạn đơn định; vì qQ và a, ta có:

(q, a) 1

3) - (A, aaabbaaaa)

+ (A, a) = A; (A, a) = A; (A, a) = A;

+ (A, b) = B;

+ (B, b) = E;

+ (E, a) = E; (E, a) = E; (E, a) = E; (E, a) = E

(A, aaabbaaaa) = E.

- (B, aaaabbaa);

+ (B, a) = D;


+ (D, a) = C;

+ (C, a) = E;

+ (E, a) = E;

+ (E, b) = ;

+ (, b) = ;

+ (, a) = .

+ (, a) = .

(B, aaaabbaa) = .

4) - w = aabaaaaa$

Ta trình bày giải thuật sử dụng automat đơn định đoán nhận w bằng bảng sau:


Bước

q

c

khởi tạo

A

a

1

A

a

2

A

b

3

B

a

4

D

a

5

C

a

6

E

a

7

E

a

8

E

$

Ta có q = E F. Vậy automat trên đoán nhận được từ w = aabaaaaa.

- w = aaaababbb$


Bước

q

c

khởi tạo

A

a

1

A

a

2

A

a

3

A

a

4

A

b

5

B

a

6

D

b

7

E

b

8

b

9

$

Ta có q = F. Vậy automat trên không đoán nhận được từ w = aaaababbb.

Ngày đăng: 16/07/2022