Hình Ảnh Minh Hoạ Sử Dụng Variogram Để Phân Cấp Tài Nguyên Trữ Lượng

dạng, các đối tượng đã biết từ trước không khác nhau nhiều thì bài toán gặp khó khăn.

- Phân tích Dengram chính là sơ đồ dạng chùm hay dạng phân nhánh cành cây được sử dụng để phản ánh mối liên hệ giữa các đối tượng từ đám đông nhiều đối tượng. Trong điều tra nghiên cứu địa chất, các nhà địa chất thường sử dụng phân tích Dengram để hỗ trợ phân nhóm các đối tượng địa chất cần nghiên cứu nhằm làm sáng tỏ mối liên quan giữa các đối tượng. Mô hình được nhiều nhà địa chất sử dụng trong nghiên cứu thạch học, cổ sinh, địa tầng, v.v. Song rất tiếc là cho đến nay các cơ sở lý thuyết này chưa được hoàn thiện. Đặc biệt là chưa có một tiêu chuẩn toán thống kê tin cậy để ghép nhóm. Do vậy trong thực tế thường xuất hiện nhiều phương án ghép nhóm khác nhau cùng một nguồn tài liệu gốc [16].

- Phân tích yếu tố chính, đây là bài toán phức tạp, dựa vào tài liệu gốc tính toán các đặc trưng thống kê (trung bình, phương sai) và thành lập ma trận hệ số tương quan giữa các yếu tố. Thể hiện được các yếu tố chính và mối tương quan giữa các yếu tố trong rất nhiều các yếu tố phản ánh đối tượng nghiên cứu. Công việc khó nhất là tìm kiếm các giá trị riêng và véc tơ riêng của ma trận hệ số tương quan. Phải tìm căn của phương trình hàm mũ bậc m (m - số các tính chất trong ma trận, có trường hợp m = 7) cao là không có khả năng, phải thực hiện một khối lượng tính toán lớn trên máy tính điện tử.

Từ những phân tích nêu trên, để phát huy ứng dụng phần mềm máy tính cho công tác nghiên cứu, luận án chỉ sử dụng mô hình toán thống kê một chiều để nhận biết các đặc trưng thống kê, toán thống kê hai chiều để xác định mối tương quan giữa Au và các thành phần có ích đi kèm.

c. Mô hình toán dựa trên cơ sở lý thuyết quá trình ngẫu nhiên

Mô hình toán dựa trên lý thuyết quá trình ngẫu nhiên được trình bày chi tiết trong [16], trong đó các tác giả cho rằng “Trong các công trình nghiên cứu

của A. B. Kazdan, A. M. Maragơdin đã chỉ ra rằng để mô tả sự biến đổi các thông số cơ bản của mỏ khoáng tốt nhất là áp dụng thuật toán trên cơ sở lý thuyết hàm ngẫu nhiên ổn định”, bao gồm: Lý thuyết đại số tuyến tính, phân tích tự tương quan, phân tích sóng dao động điều hoà và địa thống kê (hàm cấu trúc). Mô hình hàm cấu trúc được sử dụng rộng rãi và gần như mặc định cho hầu hết các phần mềm ứng dụng trong nghiên cứu địa chất.

c.1. Mô hình hàm cấu trúc

Hiện nay, địa thống kê (mà “cái đầu” là hàm cấu trúc) là thuật toán được sử dụng rộng rãi và có hiệu quả để giải quyết những vấn đề về thăm dò và khai thác, tối ưu hoá lòng đất. Cơ sở của địa thống kê được G. Matheron sáng lập vào những năm 1962 - 1963, nhưng tiền đề để tạo ra nó là các công trình nghiên cứu của giáo sư người Nam Phi D. Krige (1951-1952).

G. Matheron định nghĩa địa thống kê là sự áp dụng có tính hình thức các hàm ngẫu nhiên và sự ước lượng các hiện tượng tự nhiên [12].

Khi xét đến đặc tính không gian của đối tượng nghiên cứu, lý thuyết toán cơ bản được dùng là “lý thuyết biến số vùng”. Biến số đó biến đổi một cách liên tục từ điểm quan sát này đến điểm quan sát khác song rất khó mô hình hoá bằng một hàm thông thường. Dễ nhận thấy, giá trị trong một quan sát nào đó có liên quan đến giá trị tổng các điểm khác phân bố cách nhau một khoảng cách nhất định; ảnh hưởng của điểm ở khoảng cách xa ít hơn những điểm có khoảng cách gần nhau, thêm vào đó có thể xảy ra trường hợp mức độ ảnh hưởng còn phụ thuộc vào phương vị không gian của vị trí nghiên cứu. Để phản ảnh sự phụ thuộc này, người ta thường dùng véctơ khoảng cách (h) có hướng xác định. Mức phụ thuộc giữa các điểm đo (lấy mẫu) nằm trên một khoảng cách hi và theo hướng xác định nào đó được phản ánh bằng momen tương quan và có thể biểu diễn bằng hàm số sau:

Var Z( x1)  Z( x 2)

 2 Z( x1)  Z( x 2)

với mọi x1, x2D

Trong đó D là tập hợp con cố định trong không gian n chiều

2Z( x1) Z( x 2)

là hàm số của gia số Z(x1), Z(x2) đã được G. Matheron gọi

là Variogram (hàm cấu trúc) và được định nghĩa như là một nửa kỳ vọng toán của biến ngẫu nhiên, tức:

(h) 1 E Z

Z

( xi )

Z( xi h)

(2.24)

hoặc

(h) 1

2v 

( xi)

Z( xi h)

2dv

(2.25)

Trong đó Z(xi), Z(xi+h) là hai đại lượng ở hai điểm nghiên cứu cách nhau một khoảng cách là h.

Variogram thực nghiệm được xác định theo công thức:

1 N (h) 2

(h) 

2N (h)

Z( xi) Z( xih) 

i 1

(2.26)

Trong đó N(h): số lượng cặp điểm nghiên cứu

Sau khi xác định được các (h) thực nghiệm cần phải mô hình hoá về các mô hình lý thuyết để khai thác tính ưu việt của mô hình như luận giải về tính biến đổi, tính đẳng hướng, dị hướng của quặng hoá, giúp định hướng cho công tác luận giải mạng lưới thăm dò, bố trí công trình thăm dò, lấy mẫu, lựa chọn hình dạng và kích thước khối tính tài nguyên, trữ lượng và trợ giúp đánh giá tài nguyên, trữ lượng bằng phương pháp Kriging. Các mô hình lý thuyết có thể là mô hình cầu (spherical), hàm mũ (exponential), Gauss, hiệu ứng lỗ hổng (hole effect), v.v.

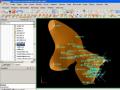
Khi xác định kích thước đới ảnh hưởng của thông số quặng hoá theo hàm Variogram là H(m), theo nhiều nhà nghiên cứu [13] diện tích được quét bởi giá trị bằng (2/3)H(m) có thể được xếp vào diện tích chắc chắn về địa chất; diện tích được quét bởi giá trị bằng H(m) có thể được xếp vào diện tích

tin cậy; diện tích được quét bởi giá trị lớn hơn H(m) có thể được xếp diện tích dự tính hoặc dự đoán (phỏng đoán), hình 2.8 [28].

Hình 2.8. Hình ảnh minh hoạ sử dụng Variogram để phân cấp tài nguyên trữ lượng “Nguồn: Snowden Mining Industry Consultans 2006” [28]

Cũng cần lưu ý rằng các (h) chỉ có kết quả tốt khi có số lượng điểm nghiên cứu đủ lớn.

Hàm cấu trúc có ưu điểm lớn là thể hiện sự biến đổi một cách toàn diện (mức độ, đặc tính, cấu trúc); khảo sát mức độ tương quan không gian và tính đẳng hướng, dị hướng của các thông số nghiên cứu mà các mô hình khác không thể thực hiện được. Hàm cấu trúc còn góp phần quyết định tính chính xác của dự báo tài nguyên và tính trữ lượng bằng Kriging.

c.2. Mô hình dựa trên lý thuyết đại số tuyến tính

Mô hình dựa trên cơ sở lý thuyết thống kê tuyến tính của C. R. Rao (linear Statistical in Reference) được các nhà địa chất Liên Xô cũ, Canada, Anh, Mỹ khai thác sử dụng trong địa chất.

Lý thuyết thống kê tuyến tính giả thuyết biến lượng các tính chất hoặc hiện tượng địa chất cần mô hình hoá trên trục không gian X không chỉ là một biến lượng ngẫu nhiên mà là một hàm ngẫu nhiên chứa đựng hai hợp phần, có thể viết:

(x)=C(x)+(x) (2.27)

Trong đó: (x): Trường thực tế quan sát được; C(x): Hợp phần có quy luật không gian;

(x): Hợp phần ngẫu nhiên.

Có rất nhiều nhà địa chất thực dụng của Liên Xô cũ như A. I. Pogomarenko (1974), M. I. Iadrenco (1973), v.v, đều có chung quan điểm rằng: hợp phần C(x) thể hiện tổng Trend chung của phông khu vực C(x) và

dị thường Ca(x) tức là:

C(x)= C(x)+Ca(x)	(2.28)
	(x)=C(x)+Ca(x)+(x)	(2.29)

Có thể bạn quan tâm!

Xem toàn bộ 162 trang tài liệu này.

Để xác định hợp phần C(x) cần áp dụng mô hình Trend theo tuyến tìm kiếm (địa hoá, v.v.).

Ưu điểm xây dựng trên cơ sở toán ngẫu nhiên để giải các bài toán phân chia dị thường địa hoá trên các tuyến tìm kiếm.

Nhược điểm bài toán phức tạp, cần phải hỗ trợ bằng các mô hình khác.

c.3. Phân tích tự tương quan

Mô hình tự tương quan được xây dựng trên cơ sở lý thuyết hàm ngẫu nhiên ổn định với giả thuyết: các giá trị hàm lượng nguyên tố phân tích được nhờ lấy mẫu với khoảng cách h trên tuyến tìm kiếm không phải là một biến lượng ngẫu nhiên mà là thực thể của hàm ngẫu nhiên.

Hàm tự tương quan định mức được tính theo công thức:

cov(Y ,Y )

K (h)

N h

f ( X ) .f ( X

i h

) 

r(h) i i h

i 1

(2.30)

2 D N h 2

Trong đó: N: Số điểm quan sát, lấy mẫu nghiên cứu; h- Số bước quan sát.

Trong một số trường hợp bên cạnh hàm tương quan định mức r(h), các nhà địa chất còn sử dụng hàm cấu trúc (h) để mô hình hoá và khai thác bổ sung cho hàm tương quan định mức. Nhờ sự giúp đỡ của hàm tương quan định mức và hàm cấu trúc có thể làm sáng tỏ mức độ dao động tổng quan về giá trị biến lượng cần nghiên cứu, xác định bán kính tự tương quan, phát hiện sự phân bố hàm lượng quặng mang tính chu kỳ hoặc cho phép tách phương sai thành hợp phần tương quan không gian và hợp phần không tương quan.

Ưu điểm nhờ đồ thị của hàm tự tương quan làm sáng tỏ mức độ dao động, bán kính tự tương quan, phân bố mang tính chu kỳ, cường độ, tốc độ, tích tụ nguyên tố.

Nhược điểm thường không sử dụng độc lập mô hình mà phải hỗ trợ của hàm cấu trúc (h) để mô hình hoá và khai thác bổ sung cho hàm tương quan định mức.

c.4. Mô hình phân tích sóng dao động điều hoà.

Kiểu mô hình này, được nhiều nhà nghiên cứu như V. Xoloviep (1940), A. Denkop (1955), v.v, áp dụng. Giả thiết gốc của mô hình là sự biến đổi quan sát được của các nguyên tố cần nghiên cứu trên tuyến tìm kiếm, thăm dò được xem như là một thực thể của hàm ngẫu nhiên có dạng:

F(x)=S(x)+n(x) (2.31)

Trong đó:

- S(x): Hàm không ngẫu nhiên (hợp phần có quy luật) nửa sóng điều hoà;

- n(x): hợp phần ngẫu nhiên.

Áp dụng thuật toán phân tích sóng dao động điều hoà cho phép tách hợp phần S(x) để làm sáng tỏ đặc tính, khuynh hướng hoặc quy luật phân bố

không gian, đồng thời có thể cải tạo hợp phần ngẫu nhiên n(x) dưới dạng hợp phần tương quan.

Ưu điểm dựa vào hàm mật độ phổ xác định các dị thường địa hoá trên các tuyến tìm kiếm.

Nhược điểm bài toán phức tạp, để giải các bài toán cần hỗ trợ bằng các mô hình khác.

Trong các mô hình toán dựa trên cơ sở lý thuyết quá trình ngẫu nhiên, mô hình hàm cấu trúc có ưu điểm nhất, phù hợp với đối tượng nghiên cứu là Au gốc phân bố đặc biệt không đồng đều. Mô hình có đặc điểm nổi trội là ngoài biết được mức độ biến đổi, còn biết được đặc tính và cấu trúc của sự biến đổi. Đây là mô hình chủ đạo được NCS tập trung nghiên cứu trong Luận án của mình.

2.2.4. Các phương pháp đánh giá tài nguyên trữ lượng khoáng sản

2.2.4.1. Các phương pháp dự báo tài nguyên chưa xác định

Trên cơ sở phân tích có hệ thống các thành tạo địa chất đã được phát hiện và nghiên cứu, các trường địa hoá - khoáng vật, trường địa vật lý và mối quan hệ của chúng với các thành tạo địa chất cho phép xác lập các tiêu chuẩn tìm kiếm, dự đoán các kiểu hình thái và kiểu quặng hoá có thể bắt gặp, đánh giá chất lượng và dự báo số lượng, tức là xác lập các tiêu chuẩn để hình thành phương pháp dự báo định lượng tài nguyên khoáng sản thích ứng với đối tượng và mức độ nghiên cứu.

Để dự báo định lượng tài nguyên chưa xác nhận, năm 1994, Allen L. Clack dựa trên kết quả các công trình nghiên cứu của Cargith và Clack (1977, 1978) và một số tác giả ở Nam Phi, Mexico, Israel, Canada đã đưa ra nhóm các phương pháp cơ bản [18] trong đánh giá tài nguyên khoáng sản bao gồm:

Nhóm các phương pháp dự báo sinh khoáng khu vực; thống kê; thực nghiệm; địa hoá vùng, khu vực quặng; địa vật lý; kinh tế; tính thẳng theo thông số quặng hoá [18].

- Nhóm các phương pháp dự báo sinh khoáng khu vực được xây dựng trên cơ sở nghiên cứu làm sáng tỏ những nút quặng nhờ sự trợ giúp của phương pháp viễn thám, địa mạo và phân tích các bản đồ sinh khoáng.

- Nhóm các phương pháp thống kê đòi hỏi sử dụng các thông tin định lượng về các tiêu chuẩn địa chất - kinh tế, địa vật lý, địa hoá và các thông số khác trên các lãnh thổ cần dự báo có liên quan đến độ chứa quặng.

- Nhóm các phương pháp dự báo thực nghiệm bao gồm phương pháp thử nghiệm đơn giản, Monte – Caclo; phương pháp chuyên gia (Den phi). Biện pháp sử dụng và tổ chức thực hiện các phương pháp Monte – Caclo và phương pháp chuyên gia rất phức tạp, đặc biệt là việc xử lý các dữ liệu trên máy tính điện tử. Phương pháp này thường được sử dụng để dự báo tài nguyên, trữ lượng dầu trong các bẫy chứa dầu mỏ.

- Nhóm các phương pháp địa hoá thường được thực hiện trên lý thuyết và thực nghiệm mối liên hệ phụ thuộc đặc trưng về sự tập trung và phân tán các nguyên tố trong khu vực cần dự báo.

- Phương pháp địa vật lý chủ yếu dựa trên cơ sở quy luật tương quan giữa hàm lượng quặng với cường độ và dạng biểu hiện các dị thường địa vật lý.

- Nhóm các phương pháp kinh tế được đặt trên cơ sở của việc phân tích động lực phát triển chiến lược gia tăng trữ lượng, tài nguyên khoáng phụ thuộc vào độ kéo dài thời gian khai thác tương đối cần đánh giá, việc đánh giá định lượng các đối tượng chuẩn và các đối tượng cần đánh giá. Các phương pháp kinh tế được áp dụng nhiều lĩnh vực dự báo tài nguyên dầu khí, còn lĩnh vực khoáng sản rắn nhìn chung ít sử dụng.