Văn Phạm Phi Ngữ Cảnh Xác Suất Từ Vựng Hóa

Mô hình văn phạm liên kết tiếng Việt - 4

Vấn đề nói trên được giải quyết bởi giải thuật trong – ngoài (Inside – Outside Algorithm) do Baker đề xuất năm 1979 cho văn phạm phi ngữ cảnh [81]. Đây thực chất là biến thể của giải thuật tiến – lùi của mô hình Markov ẩn (Hidden Markov Model – HMM). Giải thuật cho phép tính xác suất trong và xác suất ngoài cho câu vào S theo cách đệ quy.

Mô hình Markov ẩn được Manning và Schütze [87] giới thiệu, quan tâm đến dãy các quan sát O1,…, Om sản sinh bởi các luật Ni → NjN k và Ni → wj . Trong đó Oi , i = 1, m thực chất là các ký hiệu kết thúc (từ) w1,…, wm của xâu đưa vào.

Theo mô hình HMM, ma trận tham số của văn phạm phi ngữ cảnh xác suất là α [i, j, k] và β [i, r] với:

α [i, j, k] = Pr ( Ni → NjNk | G )

β [i, r] = Pr ( Ni→ r | G )

Để có thể xây dựng ma trận tham số như trên, văn phạm phi ngữ cảnh được giả thiết là ở dạng chuẩn Chomsky. Điều này không làm giảm tính tổng quát của mô hình, vì theo [63], mọi văn phạm phi ngữ cảnh có thể chuyển về dạng chuẩn Chomsky. Ràng buộc sau là bắt buộc cho các tham số :

∑ α 8i, j, k; + ∑> β 8i, r; = 1 với mọi i.

Ràng buộc này (liên quan đến ký hiệu không kết thúc thứ i trong văn phạm) cho thấy mọi khả năng áp dụng sản xuất mà vế trái là ký hiệu không kết thúc thứ i chỉ có thể sinh ra hoặc hai ký hiệu không kết thúc hoặc một ký hiệu kết thúc (do văn phạm ở dạng chuẩn Chomsky).

Dưới đây là quy ước về ký hiệu theo [87]:

Có thể bạn quan tâm!

• Mô hình văn phạm liên kết tiếng Việt - 1
• Mô hình văn phạm liên kết tiếng Việt - 2
• Cách Tiếp Cận Cấu Trúc Và Văn Phạm Phi Ngữ Cảnh
• Tiếp Cận Qua Cấu Trúc Nét Và Văn Phạm Hợp Nhất
• Mô hình văn phạm liên kết tiếng Việt - 6
• Các Định Nghĩa Hình Thức Về Văn Phạm Liên Kết

Xem toàn bộ 305 trang: Mô hình văn phạm liên kết tiếng Việt

• Tập ký hiệu không kết thúc của văn phạm được ký hiệu là { N1 ,…, Nn }. Ký hiệu đầu là N1 .
• Tập ký hiệu kết thúc của văn phạm là {w1 , …, w V }.
• Câu được phân tích w1… wm.
• wpq là bộ phận của câu cần phân tích từ từ thứ p đến từ thứ q.
• NBC ? là ký hiệu không kết thúc Nj sinh ra dãy các từ ở vị trí từ p đến q trong câu.
• αj (p, q) là xác suất ngoài.
• βj (p, q) là xác suất trong.

Xác suất trong βj (p, q) là xác suất để ký hiệu không kết thúc thứ j (Nj ) sinh ra quan sát (dãy các từ) wp,… .wq. Một cách hình thức,

βj ( p, q ) = Pr ( wpq | NBC ? , G )

Xác suất ngoài αj (p, q) là xác suất để xuất phát từ ký hiệu đầu N1 sinh ra ký hiệu không kết thúc NBC ? và các từ của xâu đưa vào nằm ngoài wp,… , wq. Một cách hình thức, ta có :

αj ( p, q ) = Pr ( w1(p-1), NBC ? , w(q+1)m | G )

Xác suất trong và xác suất ngoài là cơ sở để xây dựng giải thuật liên quan đến hai vấn đề chính trong phân tích cú pháp theo mô hình xác suất, đó là:

1.  Đoán nhận (Recognition): Tính xác suất để ký hiệu đầu N1 sinh ra dãy quan sát O trong văn phạm G. Như vậy, với giải thuật trong (Inside Algorithm), xác suất để một câu có m từ w1… wm đúng (được sản sinh bởi văn phạm G) là:

Pr ( w1m | G ) = Pr ( N1 ∗ ⇒ w1m | G ) = β1 ( 1, m )

Xác suất nói trên là xác suất đúng của câu, tức là tổng xác suất của các phân tích. Để giải quyết vấn đề nhập nhằng cần tìm ra phân tích có xác suất lớn nhất trong số các phân tích. Vấn đề này được giải quyết bằng giải thuật kiểu Viterbi trong mô hình HMM. Tương tự như giải thuật tính xác suất trong nhưng giài thuật này tìm giá trị lớn nhất thay cho tính tổng. Trong [87] đã trình bày toàn bộ giải thuật kiểu Viterbi để tìm ra cây cú pháp tốt nhất cho câu w1… .wm.

2. Huấn luyện (Training): Sau khi tìm được phân tích tốt nhất cho câu đưa vào, bộ phân tích cú pháp cần tiếp tục với giai đoạn huấn luyện. Bài toán huấn luyện có thể mô tả như sau: xác định lại xác suất của tập luật trong văn phạm G khi đã cho dãy huấn luyện gồm các câu s1, s2,…, sn. Vấn đề huấn luyện cho văn phạm phi ngữ cảnh xác suất đã được trình bày trong [87].

Theo [70], văn phạm phi ngữ cảnh xác suất có những nhược điểm sau:

• Không mô hình hóa được sự phụ thuộc giữa các cấu trúc trên cây cú pháp do xác suất của mỗi luật được tính toán hoàn toàn độc lập với nhau.
• Thiếu thông tin về từ vựng: Thông tin cú pháp có thể liên quan đến những từ đặc biệt nào đó nhưng mô hình phi ngữ cảnh lại không mô tả được. Do vậy dẫn đến nhập nhằng trong xử lý liên hợp (coordination), loại con (subcategory), sử dụng giới từ.

1.1.3.Văn phạm phi ngữ cảnh xác suất từ vựng hóa

Văn phạm phi ngữ cảnh xác suất từ vựng hóa không chỉ thể hiện cấu trúc của các ngữ mà còn cho biết mối liên hệ giữa các từ. Trong văn phạm phi ngữ cảnh xác suất từ vựng hóa (Lexicalized Probabilistic Context Free Grammar), mỗi ký hiệu không kết thúc sẽ được viết dưới dạng A(x), x = (w, t)với A là nhãn của cấu trúc. Số ký hiệu không kết thúc sẽ tăng rất mạnh, nhiều nhất tới |ν| × |τ| lần, |ν| là số lượng từ trong từ vựng và |τ| là số lượng từ loại của ngôn ngữ

Luật của văn phạm phi ngữ cảnh xác suất từ vựng hóa có dạng:

1. Luật nội tại:

P (h) → Ln(ln)…L1(l1) H(h) R1(r1) … Rm(rm)        (1.1)

Trong đó, h là cặp từ / nhãn từ loại. H là con chính của luật, sẽ thừa kế cặp từ / nhãn từ loại của nút cha P. Thành phần Ln (ln) … L1(l1) bổ nghĩa cho H ở bên trái và thành phần R1(r1)… Rm(rm) bổ nghĩa cho H ở bên phải (n hoặc m có thể bằng 0). Dãy bên trái và bên phải được mở rộng bởi ký hiệu STOP. Do vậy Ln+1 = Rm+1 = STOP

2. Luật từ vựng:

P (h) → w, P là một từ nhãn loại, h là cặp (w, t)   (1.2)

Hình 1.3. dưới đây minh họa một văn phạm phi ngữ cảnh xác suất từ vựng hóa [43].

Khi tính xác suất cho từng sản xuất, việc thêm thông tin từ vựng làm cho mẫu số trở nên vô cùng lớn, xác suất gần như bằng 0.

Để tránh số lượng tham số quá lớn, trong mô hình được Collins [43] đưa ra, xác suất của luật nội tại được tính dựa theo luật chuỗi xác suất.

Xác suất sinh ra một đối tượng bổ nghĩa có thể phụ thuộc vào một hàm bất kỳ của các đối tượng bổ nghĩa trước đó, lĩnh vực của từ trung tâm hay từ trung tâm. Do vậy, khoảng cách được [43] bổ sung vào giả thiết về tính độc lập của các từ bổ nghĩa.

Mô hình này cũng đã được nhóm Lê Thanh Hương [22] sử dụng để xây dựng bộ phân tích cú pháp tiếng Việt với nhận xét “Trong tiếng Việt các thành phần biên của các ngữ phụ thuộc vào thành phần bên cạnh nó nhiều hơn là phụ thuộc vào thành phần trung tâm”. Trong [22] đã đưa ra công thức tính xác suất luật cho các thành phần biên không có xuất hiện của khoảng cách và đề xuất công thức tính xác suất cho luật có thêm giá trị xác suất kết nối các từ ở hai bên thành phần chính của vế phải.

Tập luật (sản xuất)

Các luật nội tại

TOP → S(bought, VBD)

S(bought, VBD → NP(week, NN) NP(IBM, NNP) VP(bought, VBD)

NP(week, NN → JJ(Last, JJ) NN(week,NN)

NP(IBM, NNP) → NNP(IBM, NNP)

VP(bought, VBD) → VBD(bought,VBD) NP(Lotus,NNP)

NP(Lotus, NNP) → NNP(Lotus, NNP)

Các luật từ vựng

JJ(last, JJ) → last

NP(week, NN) → week

NNP(IBM, NNP) → IBM

VBD(bought,VBD) → bought

NP(Lotus, NNP) → Lotus

Cây ngữ cấu cho câu ”Last week IBM bought Lotus”

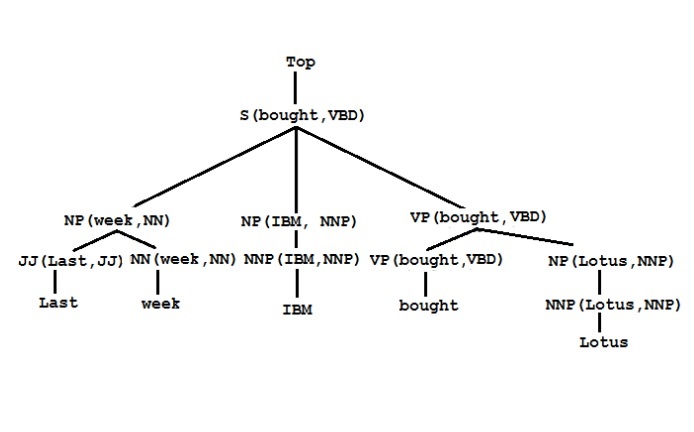
Hình 1.3. Văn phạm phi ngữ cảnh xác suất và cây ngữ cấu của câu “Last week IBM bought Lotus”

1.1.4. Văn phạm kết nối cây

Với sự ra đời của các treebank, các thao tác viết lại trên văn phạm có thể không diễn ra trên xâu nữa mà thực hiện trên cây ngữ cấu.

Phần tử cơ sở của văn phạm kết nối cây (Tree Adjoining Grammar – TAG) là cây cơ bản [69]. Các cây cơ bản được kết hợp với nhau qua hai thao tác viết lại là kết hợp và thay thế. Cây trung gian sinh ra khi áp dụng các phép thế và kết nối được gọi là các cây phân tích.

Cây phân tích đầy đủ là cây phân tích trong đó mọi nút lá đều có nhãn là ký hiệu kết thúc. Việc phân tích cú pháp cho một câu có thể hiểu là: xuất phát từ một cây cơ bản có gốc là tiên đề, tìm một cây phân tích đầy đủ có các nút lá tương ứng với dãy các từ trong câu.

Văn phạm TAG được từ vựng hóa trở thành LTAG (Lexicalized Tree Adjoining Grammar). Đây cũng là một dạng văn phạm hoàn toàn từ vựng hóa. Mỗi cây cơ bản đều có ít nhất một nút lá gắn với một đơn vị từ vựng gọi là từ neo. Ngoài ra, văn phạm còn thỏa mãn các điều kiện sau:

1. Mỗi cây khởi tạo của LTAG biểu diễn các thành phần của một từ neo (thành phần đối bổ nghĩa cho từ neo).
2. Các cây cơ bản là cực tiểu: cây khởi tạo phải có từ neo là từ trung tâm của một thành phần chính trong câu và chứa tất cả các thành phần đối bắt buộc của từ neo [20].