này được giới thiệu và trình bày trong mục Induction on decision trees, machine learning năm 1986. ID3 được xem như là một cải tiến của CLS với khả năng lựa chọn thuộc tính tốt nhất để tiếp tục triển khai cây tại mỗi bước. ID3 xây dựng cây quyết định từ trên- xuống (top -down). ID3 sử dụng độ đo Information Gain (trình bày ở 2.1.1.1) để đo tính hiệu quả của các thuộc tính phân lớp. Trong quá trình xây dựng cây quyết định theo thuật toán ID3 tại mỗi bước phát triển cây, thuộc tính được chọn để triển khai là thuộc tính có giá trị Gain lớn nhất. Hàm xây dựng cây quyết định trong thuật toán ID3 [2]
Function induce_tree (tập_ví_dụ, tập_thuộc_tính)
begin
if mọi ví dụ trong tập_ví_dụ đều nằm trong cùng một lớp then return một nút lá được gán nhãn bởi lớp đó
else if tập_thuộc_tính là rỗng then
return nút lá được gán nhãn bởi tuyển của tất cả các lớp trong tập_ví_dụ
else begin
chọn một thuộc tính P, lấy nó làm gốc cho cây hiện tại; xóa P ra khỏi tập_thuộc_tính;
với mỗi giá trị V của P
begin
tạo một nhánh của cây gán nhãn V;
Đặt vào phân_vùng các ví dụ trong tập_ví_dụ có giá trị V
V
tại thuộc tính P;
Gọi induce_tree (phân_vùng , tập_thuộc_tính), gắn kết quả
V
vào nhánh V
end
end
end
Xét ví dụ 3.1 cho thuật toán ID3:
- Gọi tập huấn luyện là S, số mẫu thuộc lớp Có ký hiệu là (+) và số mẫu thuộc lớp Không ký hiệu là (-), ta có S [9+,5-] tức tập huấn luyện S có 14 mẫu trong đó có 9 mẫu thuộc lớp Có và 5 mẫu thuộc lớp Không.
- Để xác định thuộc tính phân lớp ta cần tính Information Gain cho từng thuộc tính của mẫu huấn luyện:
o Thuộc tính Quang Cảnh
Value (QC)= {Nắng, Mưa, Âm u}
Gọi SNắng là tập các mẫu có QC=Nắng ta có SNắng=[2+,3-] Tương tự ta có SMưa= [3+,2-], SÂm u=[4+,0-]
𝐺𝑎𝑖𝑛(𝑆, 𝑄𝐶) = 𝐸𝑛𝑡𝑟𝑜𝑝𝑦(𝑆)
|𝑆𝑣|
− ∑ 𝐸𝑛𝑡𝑟𝑜𝑝𝑦(𝑆 )
𝑉𝜖𝑉𝑎𝑙𝑢𝑒(𝑄𝐶)
|𝑆| 𝑣
= 𝐸𝑛𝑡𝑟𝑜𝑝𝑦(𝑆) − 5
14
𝐸𝑛𝑡𝑟𝑜𝑝𝑦(𝑆
𝑁ắ𝑛𝑔
) − 4
14
𝐸𝑛𝑡𝑟𝑜𝑝𝑦(𝑆
Â𝑚𝑢)
5
− 14 𝐸𝑛𝑡𝑟𝑜𝑝𝑦(𝑆𝑀ư𝑎
) = 0.94 − 5
14
× 0.971 − 4
14
× 0 − 5
14
× 0.971
≈ 0.246
Tư tượng đối với các thuộc tính Nhiệt độ, Độ ẩm, Gió ta có Gain tương ứng như sau:
- Gain (S, ND) = 0.029
- Gain (S, DA) = 0.151
- Gain (S, G) = 0.048
Chọn Quang cảnh làm thuộc tính phân lớp vì có Gain lớn nhất
- Vẽ cây quyết định:
Quang Cảnh
Nắng
Mưa
Âm u
[D1, D2, D8, D9, D11]
S Nắng[2+,3-]
???
[D3, D7, D12, D13]
S Âm u[4+,0-]
Có
[D4, D5, D6, D10, D14]
S
Mưa
[3+,2-]
???
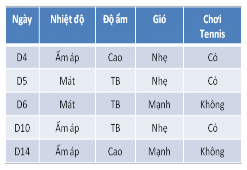
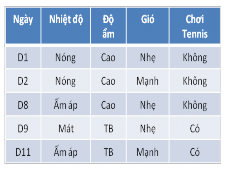
Do Quang cảnh=Nắng và Quang cảnh=Mưa chưa xác định được thuộc tính phân lớp nên ta chia tập huấn liệu thành 2 bảng như hình trên và tiếp tục tìm thuộc tính phân lớp cho 2 bảng mẫu huấn luyện. Kết quả cuối cùng ta có cây quyết định sau:
Quang Cảnh
Nắng
Mưa
Âm u
[D1, D2, D8, D9, D11]
S Nắng[2+,3-]
Độ ẩm
[D3, D7, D12,
S Âm u[4+,0-]
Có
[D4, D5, D6, D10, D14]
S
Mưa
[3+,2-]
Gió
TB
Cao
Nhẹ
Mạnh
S TB[2+,0-]
Có
S cao[0+,3-]
không
S
Nhẹ
[3+,0-]
Có
S Mạnh[0+,2-]
không
Từ cây quyết định trên tạo ra các luật:
– R1: IF QC=Âm u THEN Chơi Tennis=Có.
– R2: IF QC=Nắng AND Độ ẩm=TB THEN Chơi Tennis=Có.
– R3: IF QC=Nắng AND Độ ẩm=Cao THEN Chơi Tennis=Không.
– R4: IF QC=Mưa AND Gió=Nhẹ THEN Chơi Tennis=Có
– R5: IF QC=Mưa AND Gió=Mạnh THEN Chơi Tennis=Không
Nhận xét: Với việc tính toán giá trị Gain để lựa chọn thuộc tính tối ưu cho việc triển khai cây, thuật toán ID3 được xem là một cải tiến của thuật toán CLS. Tuy nhiên thuật toán ID3 còn các vấn đề chưa được giải quyết như sau:
o Vấn đề overfitting.
o Độ đo Information Gain chưa thật sự tốt vì còn thiên về các thuộc tính có nhiều giá trị.
o Xử lý các thuộc tính có kiểu giá trị liên tục (ví dụ như kiểu số thực).
o Xử lý các bộ học thiếu giá trị thuộc tính (missing-value attributes).
o Xử lý các thuộc tính có chi phí (cost) khác nhau.
o Vấn đề này sẽ được giải quyết trong thuật toán C4.5 sau đây.
2.1.2.2. Thuật toán C4.5
Thuật toán C4.5 cũng được tác giả Quinlan phát triển và công bố vào năm 1996. Thuật toán này là một thuật toán được cải tiến từ thuật toán ID3 và giải quyết hầu hết các vấn đề mà ID3 chưa giải quyết như đã nêu trên. Nó thực hiện phân lớp tập mẫu dữ liệu theo chiến lược ưu tiên theo chiều sâu (Depth - First).
Thuật toán xây dựng cây quyết định C4.5
Mô tả thuật toán dưới dạng giả mã như sau:
Function xay_dung_cay(T)
{
If
Else
For
nhất>; If For - Nếu N.test là thuộc tính liên tục tách theo ngưỡng ở bước 5 - Nếu N.test là thuộc tính phân loại rời rạc tách theo các giá trị của thuộc tính này. ) { If } }
2.1.2.3. Một số cài tiến của thuật toán C4.5 so với thuật toán ID3 Chọn độ đo Gain Ratio Thuật toán ID3 sử dụng độ đo Information Gain để tìm thuộc tính phân lớp tốt nhất nhưng xu hướng của Information Gain là ưu tiên chọn thuộc tính có nhiều giá trị làm thuộc tính phân lớp. Thật vậy, ta xét ví dụ với tập huấn luyện sau: Outlook Temp Humidity Windy Play A Hot High Weak No A Hot High Strong No B Hot High Weak Yes E Mild High Weak Yes A Cool Normal Weak Yes B Cool Normal Strong No E Cool Normal Strong Yes A Mild High Weak No D Cool Normal Weak Yes E Mild Normal Weak Yes Có thể bạn quan tâm! Xem toàn bộ 80 trang tài liệu này. Mild Normal Strong Yes B Mild High Strong Yes C Hot Normal Weak Yes D Mild High Strong No Test bằng Tool WEKA ta được kết quả sau: Id3 Outlook = A | Humidity = High: No Test bằng WEKA C4.5 Humidity = High | Outlook = A: No (3.0) | Humidity = Normal: Yes Outlook = B | Temp = Hot: Yes | Temp = Mild: Yes | Temp = Cool: No Outlook = E: Yes Outlook = D | Temp = Hot: null | Temp = Mild: No | Temp = Cool: Yes Outlook = C: Yes | Outlook = B: Yes (2.0) | Outlook = E: Yes (1.0) | Outlook = D: No (1.0) | Outlook = C: No (0.0) Humidity = Normal: Yes (7.0/1.0) Rò ràng Information Gain chọn thuộc tính có nhiều giá trị (Outlook) làm thuộc tính phân lớp. Kết quả cho cây quyết định phức tạp hơn, sinh ra nhiều luật hơn. Trong thuật toán C4.5, tác giả Quinlan đã giải quyết vấn đề này bằng cách sử dụng 1 độ đo khác là Gain Ratio, làm giảm ảnh hưởng của các thuộc tính có nhiều giá trị. Xử lý các thuộc tính có kiểu giá trị liên tục Thuộc tính kiểu giá trị liên tục là: Ngày Quang Cảnh Nhiệt độ Độ ẩm Gió Chơi Tennis D1 Nắng 85 85 Nhẹ Không D2 Nắng 80 90 Mạnh Không D3 Âm u 83 78 Nhẹ Có D4 Mưa 70 96 Nhẹ Có D5 Mưa 68 80 Nhẹ Có D6 Mưa 65 70 Mạnh Không D7 Âm u 64 65 Mạnh Có D8 Nắng 72 95 Nhẹ Không D9 Nắng 69 70 Nhẹ Có D10 Mưa 75 80 Nhẹ Có D11 Nắng 75 70 Mạnh Có D12 Âm u 72 90 Mạnh Có D13 Âm u 81 75 Nhẹ Có D14 Mưa 71 80 Mạnh Không Trong thuật toán ID3 không phân biệt thuộc tính kiểu giá trị liên tục và thuộc tính kiểu giá trị rời rạc, mà chỉ xem thuộc tính kiểu giá trị liên tục như một thuộc tính có nhiều giá trị, và phạm phải khuyết điểm trên là ưu tiên chọn thuộc tính này làm thuộc tính phân lớp. Giả sử thuộc tính A có các giá trị v1, v2,…, vN, thuật toán C4.5 đã giải quyết vấn đề này như sau: Trước tiên, sắp xếp các giá trị của thuộc tính A tăng dần ví dụ như từ v1, v2,.., vN. Chia giá trị của thuộc tính A thành N-1 “ngưỡng” Tính Information Gain ứng với N-1 “ngưỡng”. Chọn “ngưỡng” có Information Gain cao nhất làm “ngưỡng” tốt nhất của A, Gain (S, A) là giá trị Gain cao nhất của “ngưỡng” chọn. Nhận xét: Việc tìm ngưỡng theo thuật toán C4.5 rất tốn thời gian để tính Gain cho N-1 ngưỡng. Sau có nhiều tác giả đã nghiên cứu để tìm cách tìm ngưỡng nhanh hơn như Fayyad (1991), Utgoff, Brodley, Murthy et al. Làm việc với thuộc tính thiếu giá trị Thuật toán xây dựng dựa vào giả thuyết tất cả các mẫu dữ liệu có đủ các thuộc tính. Nhưng trong thực tế, xảy ra hiện tượng dữ liệu bị thiếu, tức là ở một số mẫu dữ liệu có những thuộc tính không được xác định hoặc mâu thuẫn, hoặc không bình thường. Ta xem xét kỹ hơn với trường hợp dữ liệu bị thiếu. Đơn giản nhất là không đưa các mẫu với các giá trị bị thiếu vào, nếu làm như vậy thì có thể dẫn đến tình trạng thiếu các mẫu học. Một số cách khác được đề xuất ở thuật toán C4.5 như sau: Giả sử thuộc tính A là một ứng cử cho thuộc tính kiểm tra ở nút n; Xử lý thế nào với bộ X thiếu giá trị đối với thuộc tính A (tức là XA là không xác định); Gọi Sn là tập các mẫu học gắn với nút n có giá trị đối với thuộc tính A; – Giải pháp 1: XA là giá trị phổ biến nhất đối với thuộc tính A trong số các bộ thuộc tập Sn; – Giải pháp 2: XA là giá trị phổ biến nhất đối với thuộc tính A trong số các bộ Sn có cùng phân lớp với X; – Giải pháp 3: Tính xác suất pv đối với mỗi giá trị có thể V của thuộc tính A; Gán phần pv của bộ X đối với nhánh tương ứng của nút n; Giá trị pv này được dùng tính Gain và hơn nữa để chia nhỏ nhánh tiếp theo của cây nếu có thuộc tính thứ 2 có lỗi (thiếu giá trị) Xét ví dụ sau: Ngày Quang Cảnh Nhiệt độ Độ ẩm Gió Chơi Tennis D1 Nắng Nóng Cao Nhẹ Không D2 Nắng Nóng Cao Mạnh Không D3 Âm u Nóng Cao Nhẹ Có D4 Mưa Ấm áp Cao Nhẹ Có D5 Mưa Mát TB ??? Có D6 Mưa Mát TB Mạnh Không D7 Âm u Mát TB Mạnh Có D8 Nắng Ấm áp Cao Nhẹ Không D9 Nắng Mát TB Nhẹ Có D10 Mưa Ấm áp TB Nhẹ Có D11 Nắng Ấm áp TB Mạnh Có D12 Âm u Ấm áp Cao Mạnh Có D13 Âm u Nóng TB Nhẹ Có D14 Mưa Ấm áp Cao Mạnh Không Tại mẫu huấn luyện D5 có thuộc tính không rò giá trị là thuộc tính Gió, theo 3 giải pháp trên ta tìm giá trị cho thuộc tính ở mẫu này như sau:
Kỹ thuật cây quyết định hồi quy trong phân tích và dự báo rủi ro tín dụng tại ngân hàng TMCP Sài Gòn – Hà Nội (HSB), chi nhánh Thái Nguyên - 2
Khái Niệm Và Mục Tiêu Của Quản Trị Rủi Ro Tín Dụng
Chiến Lược Cơ Bản Để Xây Dựng Cây Quyết Định
Phương Pháp Chuyên Gia Trong Xếp Hạng Tín Dụng
Đặc Điểm Sản Phẩm Gửi Tiết Kiệm Ngân Hàng Shb
Phân Tích Và Dự Báo Rủi Ro Tín Dụng Tại Ngân Hàng Tmcp Sài Gòn – Hà NộiA