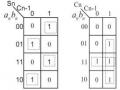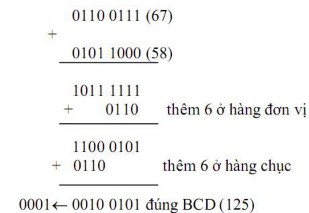
Trừ các số BCD:
Cũng theo quy luật trừ nhị phân. Nếu số bị trừ nhỏ hơn số trừ thì phải mượn 1 ở hàng có nghĩa trên mà có giá trị là 10 nhị phân ở hàng đang bị trừ (giống số mượn ở phép trừ thập phân). . Để tiện việc sắp xếp ta chuyển 1 ở hàng có nghĩa kế trên xuống hàng đang bị trừ thành 1010 (=10 thập phân) rồi cộng vào với số bị trừ trước khi thực hiện phép trừ.
Ví dụ 1.29:
Trừ các số BCD sau:
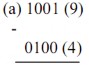

Giải:

1.5.5. Biểu diễn ký tự
Tuỳ theo các hệ thống khác nhau, có thể sử dụng các bảng mã khác nhau: ASCII, EBCDIC, UNICODE,....Các hệ thống trước đây thường dùng bảng mã ASCII (American Standard Codes for Information Interchange) để biểu diễn các chữ, số và một số dấu thường dùng mà ta gọi chung là ký tự. Mỗi ký tự được biểu diễn bởi 7 bittrong một Byte. Hiện nay, một trong các bảng mã thông dụng được dùng là Unicode, trong bảng mã này, mỗi ký tự được mã hoá bởi 2 Byte.
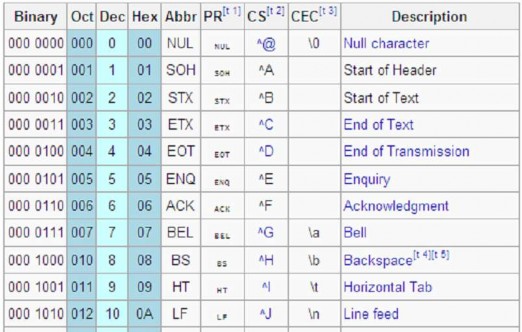
Bảng mã ASCII (American Standard Code for Information Interchange) Bảng 1. 4. Bảng mã ASCII - Một số ký tự điều khiển
Bảng 1. 5. Bảng mã ASCII - Các ký tự in được
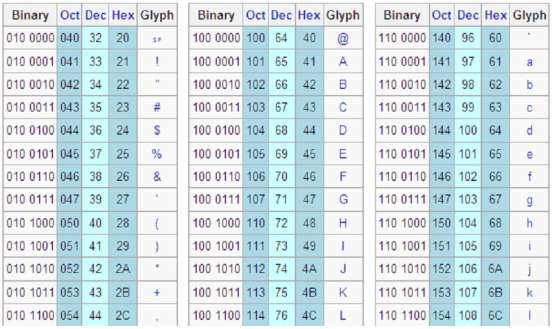
Bảng mã ASCII là bảng mã các ký tự chuẩn tiếng Anh dùng cho trao đổi dữ liệu giữa các hệ thống tính toán. Bảng mã ASCII sử dụng 8 bít để biểu diễn 1 ký tự, cho phép định nghĩa tổng số 256 ký tự, đánh số từ 0 đến 255. 32 ký tự đầu tiên và ký tự số 127 là các ký tự điều khiển (không in ra được). Các ký tự từ số 32 đến 126 là các ký tự có thể in được (gồm cả dấu trắng). Các vị trí còn lại trong bảng (128-255) để
dành cho sử dụng trong tương lai. Bảng dưới đây lần lượt là minh hoạ các ký tự điều khiển và các ký tự in được của bảng mã ASCII.
Bộ mã hợp nhất Unicode:
- Do các hãng máy tính hàng đầu thế giới kết hợp thiết kế.
- Bộ mã 16 bit có thể xây dựng bộ mã toàn cầu 216 ký tự với 128 ký tự đầu có mã trùng mã trong bảng mã ASCII.
- Có hỗ trợ các ký tự Tiếng Việt.
Biểu diễn hình ảnh
Hình ảnh cũng có thể xử lý bằng máy tính. Khác với hình ảnh thông thường, hình ảnh trong máy tính được mã hoá dưới dạng nhị phân. Có rất nhiều kiểu mã hoá ảnh trong đó hai kiểu thông dụng nhất là. Ảnh bitmap (nghĩa là bản đồ các bít) thể hiện ảnh như một lưới điểm. Như vậy mỗi điểm sẽ phải nằm trong một hàng và một cột nào đó trong lưới, ngoài ra màu của điểm cũng được mã hoá. Các ảnh khí tượng do các vệ tinh chụp gửi về, ảnh phong cảnh, chân dung đều có thể thể hiện theo kiểu này. Ta cũng có thể đưa một ảnh bất kỳ vào máy dưới dạng bitmap bằng máy quét ảnh (scanner), máy quay video số (digital video camera) hay máy chụp ảnh số (digital camera)... Nói chung dữ liệu ảnh này là dữ liệu lớn. Vì vậy, người ta thường sử dụng các kỹ thuật nén ảnh trước khi đưa vào máy lưu trữ và khôi phục ảnh khi trình bày. Có rất nhiều chuẩn ảnh khác nhau, chủ yếu khác nhau ở cách tổ chức để nén được ảnh mà vẫn giữ được chất lượng và thể hiện được các hiệu ứng ảnh. Còn lúc hiển thị để xem thì ảnh sẽ được khôi phục dưới dạng bitmap. Ảnh thể hiện theo từng điểm còn gọi là ảnh raster.
Kiểu thứ 2 thể hiện ảnh theo cách vẽ. Kiểu này chỉ phù hợp với các ảnh có thành phần là các điểm rời rạc, các đường hoặc hình thể hiện bằng các đường biên như bản vẽ kiến trúc, các bản vẽ kỹ thuật, bản đồ. Cách lưu trữ là lưu thông tin về các thành phần của ảnh. Đối với một đoạn thẳng thì chỉ lưu toạ độ các đầu mút, đối với một hình tròn thì chỉ lưu toạ độ tâm và bán kính... Vì thế các ảnh này thường gọn gàng và dễ phóng to thu nhỏ (vì chỉ dùng các phép biến đổi toạ độ). Các ảnh kiểu này gọi là ảnh vector.

Hình 1. 24. Hình Bitmap
Biểu diễn âm thanh
Âm thanh cũng có thể được xử lý bằng máy tính. Cũng có nhiều phương pháp mã hoá âm thanh. Cách đơn giản nhất là mã hoá bằng cách xấp xỉ dao động sóng âm bằng một chuỗi các byte thể hiện biên độ dao dộng tương ứng theo từng khoảng thời gian bằng nhau. Dĩ nhiên các đơn vị thời gian này cần phải đủ nhỏ để không làm nghèo âm thanh. Đơn vị thời gian này gọi là chu kỳ lấy mẫu. Hình vẽ dưới đây minh hoạ cách lưu trữ xấp xỉ sóng âm, theo đó sẽ lưu lại dãy các giá trị sau: Khi phát, một mạch điện sẽ khôi phục lại sóng âm với một sai lệch chấp nhận được. Một cách khác là phân tích dao động âm thanh thành tổng các dao động điều hoà (các dao động hình sin với tần số và biên độ khác nhau) và chỉ lưu lại các đặc trưng về tần số, và biên độ. Còn có nhiều cách mã hoá âm thanh dựa theo những nguyên lý nén dữ liệu rất hiệu quả Việc số hoá âm thanh cũng được thực hiện nhờ các thiết bị chuyên dụng.
Xử lý âm thanh trên máy tính gồm những việc sau:
- Thu và mã hoá âm.
- Biên tập (sửa chữa, ghép, cắt).
- Phân tích (tìm các đặc trưng để nhận dạng tiếng nói). Một số máy tính đã có thể nghe được các lệnh đơn giản. Các máy điện thoại di động hiện nay đã có khả năng nhận dạng tiếng nói.
- Tổng hợp tiếng nói. Ở mức độ đơn giản máy tính có thể đọc văn bản thành lời.
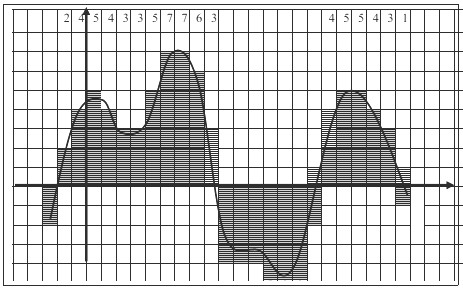
Hình 1. 25. Số hóa âm thanh.
1.6. Đại số Boolean
1.6.1. Các phép toán và định lý của đại số Boolean
- Biến logic: Đại lượng biểu diễn bằng ký hiệu nào đó chỉ lấy giá trị "1" hoặc "0".
- Hàm logic: Biểu diễn nhóm các biến logic liên hệ với nhau thông qua các phép toán logic, một hàm logic cho dù là đơn giản hay phức tạp cũng chỉ nhận giá trị hoặc là "1" hoặc là "0".
- Các phép toán logic: có 3 phép toán cơ bản. Phép nhân (và) - kí hiệu là AND.
Phép cộng (hoặc) - kí hiệu là OR. Phép phủ định (đảo) - kí hiệu là NOT Đại số logic
Để mô tả các mạch điện được xây dựng từ các cổng, chúng ta cần sử dụng đại số logic (Boolean algebra). Hàm logic có một hoặc một số biến vào, nó sẽ sinh ra một giá trị kết quả phụ thuộc vào các biến vào này. Một hàm f đơn giản có thể được định nghĩa như sau: f(A) bằng 1 nếu A bằng 0 và f(A) bằng 0 nếu A bằng 1. Hàm này chính là hàm NOT.
Bởi vì một hàm logic n biến chỉ có ![]() tập có thể các giá trị biến vào, cho nên hoàn toàn có thể mô tả hàm bằng một bảng có
tập có thể các giá trị biến vào, cho nên hoàn toàn có thể mô tả hàm bằng một bảng có ![]() hàng, mỗi hàm cho giá trị của hàm ứng với mỗi tổ hợp khác nhau của các biến vào. Bảng như vậy được gọi là bảng chân lý (Truth table) hay bảng sự thật.
hàng, mỗi hàm cho giá trị của hàm ứng với mỗi tổ hợp khác nhau của các biến vào. Bảng như vậy được gọi là bảng chân lý (Truth table) hay bảng sự thật.
![]()
Nếu chúng ta thống nhất liệt kê các hàng của bảng chân lý theo thứ tự số học (cơ số 2), nghĩa là cho 2 biến theo thứ tự 00, 01, 10 và 11 thì hàm hoàn toàn có thể được mô tả bởi một số nhị phân bit. Số này nhận được bằng cách đọc kết quả từ
bảng chân lý theo cột, từ trên xuống dưới. Mặc dù hầu hết các hàm logic có thể được biểu diễn bằng bảng chân lý, nhưng khi số biến tăng lên, cách biểu diễn này trở nên bất tiện vì cồng kềnh. Trong trường hợp đó người ta thường sử dụng một cách biểu diễn khác, được trình bày dưới đây.
Bảng 1. 6. Bảng chân lý của hàm f(A,B)=A+B
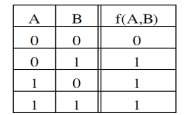
Chúng ta có thể nhận thấy rằng mọi hàm logic có thể được chỉ rò bằng cách cho biết những tổ hợp biến vào làm cho giá trị ra bằng 1. Chúng ta quy ước sẽ ghi một dấu gạch ngang bên trên các biến để chỉ ra rằng các giá trị này được đảo. Ngoài ra sẽ dùng các dấu phép toán nhân và cộng thông thường (dấu . và dấu +) để chỉ các phép toán logic AND và OR. Nếu như vậy việc viết ![]() C có nghĩa là A=1, B=0 và C=1. Tương tự như vậy
C có nghĩa là A=1, B=0 và C=1. Tương tự như vậy ![]() +
+![]() có nghĩa là (A=1 và B=0) or (B=1 and C=0).
có nghĩa là (A=1 và B=0) or (B=1 and C=0).
Một hàm n biến vì thế có thể được mô tả bằng cách cho một tổng của nhiều
nhất là ![]() hạng thức tích n biến. Phát biểu này đặc biệt quan trọng bởi nó dẫn trực tiếp tới việc thực hiện hàm bằng việc sử dụng các cổng theo chuẩn.
hạng thức tích n biến. Phát biểu này đặc biệt quan trọng bởi nó dẫn trực tiếp tới việc thực hiện hàm bằng việc sử dụng các cổng theo chuẩn.
![]()
![]()
Bảng 1. 7. Một số định luật của đại số logic
Dạng AND | Dạng OR | |
Định luật đồng nhất thức | 1A=A | 0+A=A |
Định luật về số 0 (Null law) | 0A=0 | 1+A=1 |
Định luật lũy đẳng (Idempotent law) | AA=A | A+A=A |
Định luật đảo (Inverse law) | A =0 | A+ =1 |
Định luật giao hoán (Commutative law) | AB=BA | A+B=B+A |
Định luật kết hợp (Associative law) | (AB)C=A(BC) | (A+B)+C=A+(B+C) |
Định luật phân phối (Distributive law) | A+BC=(A+B)(A+C) | A(B+C)=AB+AC |
Định luật hấp thụ (Absorption law) | A(A+B)=A | A+AB=A |
Định luật De Morgan | + |
|
Có thể bạn quan tâm!
-
 Các Thành Phần Cơ Bản Trong Máy Tính Cấu Trúc Chung Của Máy Tính Điện Tử
Các Thành Phần Cơ Bản Trong Máy Tính Cấu Trúc Chung Của Máy Tính Điện Tử -
 Kiến trúc máy tính - 4
Kiến trúc máy tính - 4 -
 Kiến trúc máy tính - 5
Kiến trúc máy tính - 5 -
 Hàm Logic Và Phương Pháp Biểu Diễn Hàm Logic Các Phương Pháp Biểu Diễn Hàm Logic
Hàm Logic Và Phương Pháp Biểu Diễn Hàm Logic Các Phương Pháp Biểu Diễn Hàm Logic -
 Kiến trúc máy tính - 8
Kiến trúc máy tính - 8 -
 Kiến trúc máy tính - 9
Kiến trúc máy tính - 9
Xem toàn bộ 233 trang tài liệu này.
![]()
![]()
1.6.2. Các cổng logic
a) Hàm AND (Và)
Đối với hàm AND giá trị của hàm chỉ bằng 1 khi các biến của nó đều bằng 1; hay chỉ cần có một biến bằng 0 hàm sẽ có giá trị bằng 0.
Hình 1. 26. Hàm AND
Các IC AND thông dụng
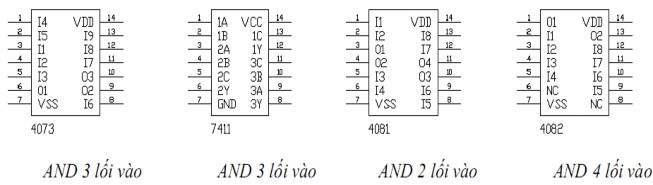
Hình 1. 27. Các IC AND
b) Hàm OR (Hoặc)
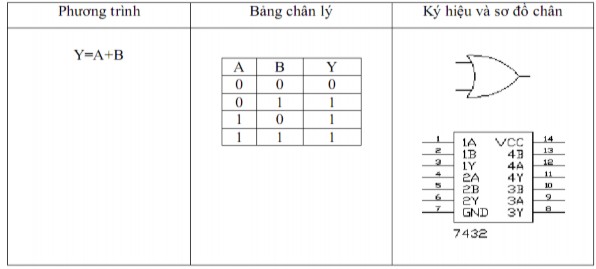
Hình 1. 28. Hàm OR
Đối với hàm OR giá trị của hàm chỉ bằng 0 khi các biến của nó đều bằng 0; hay chỉ cần có một biến bằng 1 hàm sẽ có giá trị bằng 1
Các IC OR thông dụng khác
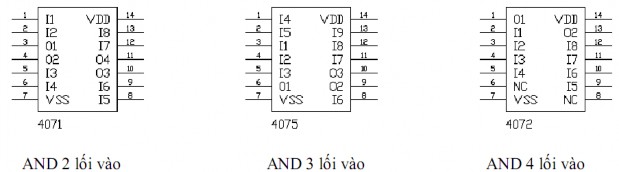
Hình 1. 29. Các IC OR
c) Hàm NOT (Đảo)
Đối với hàm NOT giá trị của hàm sẽ là đảo của giá trị biến. Khi biến có giá trị bằng 0 thì hàm bằng 1 ngược lại khi biến bằng 1 thì hàm có giá trị bằng 0.
Hình 1. 30. Hàm NOT
d) Hàm XOR (Hoặc tuyệt đối)
Hình 1. 31. Hàm XOR
Ta thấy giá trị của hàm sẽ bằng 1 khi các biến có giá trị khác nhau. Ngược lại giá trị của hàm có giá trị bằng 0 khi giá trị của các biến là bằng nhau (cùng bằng 0 hay 1).
e) Hàm NOR (Hoặc đảo)