Cú Pháp Và Ngữ Nghĩa Của Logic Mệnh Đề

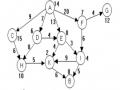
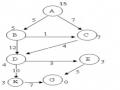
2.23. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* tìm đường đi ngắn nhất từ A tới

G. Trọng số gán tại các đỉnh là giá trị hàm đánh giá tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2.24. Cho các bài toán và toán tử sau: R1 a →c, e, l

R2 c →g, h R3 a →h, b R4 l →b, d R5 l→j, f R6 g →i R7 k →n R8 b →m, n

Tập các trạng thái kết thúc T = {i, n, m}. Bài toán gốc là a.

1. Xây dựng đồ thị và/hoặc tương ứng với các bài toán và toán tử.

2. Thực hiện từng bước giải thuật tìm kiếm trên đồ thị và/hoặc để trả lời câu hỏi bài toán a có giải được hay không?

2.25. Cho các bài toán và toán tử sau: R1 a →d, e, f

R2 a →d, k R3 a →g, h R4 d →b, c R5 f →i R6 f →c, j R7 k →e, l

Có thể bạn quan tâm!

Xem toàn bộ 272 trang tài liệu này.

R8 k →h

Tập các trạng thái kết thúc T = {b, c, e, j, l}. Bài toán gốc là a.

1. Xây dựng đồ thị và/hoặc tương ứng với các bài toán và toán tử.

2. Thực hiện từng bước giải thuật tìm kiếm trên đồ thị và/hoặc để trả lời câu hỏi bài toán a có giải được hay không?

æç 0 4

¥ ¥ ¥ ¥ ö÷

ççç 4 0 7 ¥ ¥

3 ÷÷

çç¥

7 0 3 8 6 ÷÷

çç¥ ¥

3 0 5

¥ ÷÷

ç¥ ¥

8 5 0 2 ÷÷

çè¥

3 6 ¥

2 0 ÷÷ø

2.26. Cho ma trận kề A= (aij) biểu diễn một đồ thị vô hướng G = (V,E) dưới đây: trong đó aij=  nếu (i,j)E, ngược lại aij là chi phí để đi từ đỉnh i sang đỉnh j.

1. Hãy tìm đường đi từ đỉnh 1 sang đỉnh 4 theo các phương pháp tìm kiếm rộng và tìm kiếm sâu.

2. Tìm đường đi ngắn nhất từ đỉnh 1 sang đỉnh 4

2.27. Người ta sử dụng hai bình chứa có dung tích lần lượt là 3 lít và 4 lít để đong 2 lít nước. Giả sử lượng nước được lấy từ vòi không hạn chế và công để lấy nước từ vòi cho đầy một bình là 3, công để đổ nước trong một bình ra ngoài là 2 và đổ nước từ bình này sang bình khác thì tốn công là 5.

Hãy chỉ ra quá trình tìm kiếm lời giải bằng phương pháp tìm kiếm theo bề rộng và tìm kiếm leo đồi sao cho công nhỏ nhất.

2.28. Đại dương được xem như là một mặt phẳng toạ độ trên đó có n hòn đảo với toạ độ lần lượt là (x1, y1), (x2, y2), …, (xn, yn). Một chiếc ca nô xuất phát từ đảo d1 muốn tuần tra đến đảo d2. Bình xăng của ca nô chỉ chứa đủ xăng để đi được một quãng đường dài không quá m (km). Trên đường đi ca nô có thể ghé một số đảo nào đó để tiếp thêm xăng, lúc này ca nô được tiếp thêm xăng đầy bình chứa. Hãy chỉ ra một đường đi từ đảo d1 đến đảo d2 sao cho số lần ghé đảo trung gian để tiếp thêm xăng là ít nhất.

2.29. Một mạng lưới giao thông giữa n thành phố (các thành phố được đánh số từ 1 đến n) được cho bởi ma trận a=(aij)n*n, trong đó:

0, nếu không có đường đi trực tiếp từ i đến j

aij= 1, nếu có đường đi trực tiếp từ i đến j và là đường đi an toàn

2, nếu có đường đi trực tiếp từ i đến j nhưng phải qua một chặng đường nguy hiểm

Quy ước: aii=1, i =1..n

Cho trước hai thành phố i0, i1. hãy tìm một đường đi từ i0 đến i1 sao cho số chặng đường nguy hiểm phải đi qua là ít nhất.

2.30. Cho bảng vuông gồm m*n ô. Trên mỗi ô ghi số 0 hay 1.

1. Từ một ô nào đó có thể chuyển sang ô chứa số 1 có chung cạnh với nó. giả sử đang ở ô (h,c). Hãy tìm xem có cách di chuyển từ ô này ra một ô ở mép bảng hay không? Tìm cách chuyển qua ít ô nhất.

2. Một miền của bảng là tập hợp các ô có chung cạnh và có cùng giá trị. hãy đếm xem bảng có bao nhiêu miền. miền lớn nhất có bao nhiêu ô.

3. Cho phép thay đổi giá trị tất cả các ô trong cùng một miền. Hãy xác định miền cần thay đổi để số miền giảm nhiều nhất.

4. Hãy xác định miền cần thay đổi để thu được một miền mới lớn nhất.

2.31. Một toà lâu đài được mô tả bằng một hình chữ nhật có m*n ô. Giữa các ô có một số bức tưòng ngăn cách chia lâu đài thành các phòng. Như vậy, mỗi phòng tương ứng với tập các ô thông nhau. Tại ô (i,j), cho biết thông tin có tường ngăn giữa ô này với bốn ô kề với nó không bởi giá trị aij là một số nhị phân 4 chữ số tương ứng ô (i,j) có

(1) hoặc không có (0) tường ở phía Tây, Bắc, Đông, Nam. Ví dụ aij = 1001 có nghĩa là ô (i,j) có tường ở phía Tây và Nam, nhưng không có tường ở phía Bắc và Đông. Hãy viết chương trình thực hiện các yêu cầu sau:

Đếm số phòng của toà lâu đài.

1. Cho biết phòng lớn nhất có diện tích là bao nhiêu ô.

2. Cho biết nên phá bức tường ngăn hai phòng nào để được một phòng mới có diện tích lớn nhất.

2.32. Một sân chơi hình chữ nhật gồm m*n ô đơn vị. Trên mỗi ô (i,j) có đóng các trụ bê tông chiều cao aij. Giả thiết nước không thấm qua được các cạnh giữa hai trụ bê tông kề nhau. Sau một trận mưa đủ lớn, hãy tính nước đọng lại trên sân.

2.33. Cho đồ thị trạng thái. Hãy sử dụng thuật toán Nhánh cận để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2.34. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2.35. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* để tìm đường đi ngắn nhất từ đỉnh uo=A đến đỉnh B. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

K 4

2.36. Cho đồ thị trạng thái. Hãy sử dụng thuật toán A* tìm đường đi ngắn nhất từ A tới

G. Trọng số gán tại các đỉnh là giá trị hàm đánh giá tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2.37. Cho đồ thị trạng thái trong hình bên dưới. Hãy sử dụng thuật toán sâu lặp để tìm đường đi từ đỉnh uo=A đến đỉnh F với độ sâu d=3 theo thứ tự tăng dần của trọng số các đỉnh. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2.38. Cho đồ thị trạng thái.

1. Hãy sử dụng thuật toán tốt nhất-đầu tiên để tìm đường đi từ đỉnh uo=A đến đỉnh G. Trọng số gắn tại các đỉnh xác định giá trị của hàm h tại đỉnh đó. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2. hãy sử dụng thuật toán sâu lặp để tìm đường đi từ A đến G với độ sâu d=1 theo thứ tự tăng dần của trọng số các đỉnh. Yêu cầu mô phỏng từng bước quá trình tìm kiếm.

2.39. Hãy cài đặt thuật toán tìm kiếm chiều rộng.

2.40. Hãy cài đặt thuật toán tìm kiếm chiều sâu.

2.41. Hãy cài đặt thuật toán tìm kiếm tốt nhất- đầu tiên.

2.42. Hãy cài đặt thuật toán tìm kiếm leo đồi.

2.43. Hãy cài đặt thuật toán A*.

2.44. Hãy cài đặt thuật toán Nhánh _cận.

2.45. Hãy cài đặt thuật toán tìm đường đi từ đỉnh i0 đến đỉnh j0 trong đồ thị bất kỳ.

CHƯƠNG 3. LOGIC MỆNH ĐỀ

Logic mệnh đề là một ngôn ngữ biểu diễn tri thức đơn giản, có khả năng biểu diễn hẹp, nhưng thuận lợi cho ta làm quen với nhiều khái niệm quan trọng trong logic, đặc biệt trong logic vị từ sẽ được nghiên cứu trong chương sau.

3.1. Biểu diễn tri thức

Con người sống trong môi trường có thể nhận thức được thế giới nhờ các giác quan (tai, mắt và các bộ phận khác), sử dụng các tri thức tích luỹ được và nhờ khả năng lập luận, suy diễn, con người có thể đưa ra các hành động hợp lý cho công việc mà con người đang làm. Một mục tiêu của TTNT ứng dụng là thiết kế các tác nhân thông minh (intelligent agent) cũng có khả năng đó như con người. Chúng ta có thể hiểu tác nhân thông minh là bất cứ cái gì có thể nhận thức được môi trường thông qua các bộ cảm nhận (sensors) và đưa ra hành động hợp lý đáp ứng lại môi trường thông qua bộ phận hành động (effectors). Các robots, các softbot (software robot), các hệ chuyên gia,... là các ví dụ về tác nhân thông minh. Các tác nhân thông minh cần phải có tri thức về thế giới hiện thực mới có thể đưa ra các quyết định đúng đắn.

Thành phần trung tâm của các tác nhân dựa trên tri thức (knowledge-based agent), còn được gọi là hệ dựa trên tri thức (knowledge-based system) hoặc đơn giản là hệ tri thức, là CSTT. CSTT là một tập hợp các tri thức được biểu diễn dưới dạng nào đó. Mỗi khi nhận được các thông tin đưa vào, tác nhân cần có khả năng suy diễn để đưa ra các câu trả lời, các hành động hợp lý, đúng đắn. Nhiệm vụ này được thực hiện bởi bộ suy diễn. Bộ suy diễn là thành phần cơ bản khác của các hệ tri thức. Như vậy hệ tri thức bảo trì một CSTT và được trang bị một thủ tục suy diễn. Mỗi khi tiếp nhận được các sự kiện từ môi trường, thủ tục suy diễn thực hiện quá trình liên kết các sự kiện với các tri thức trong CSTT để rút ra các câu trả lời, hoặc các hành động hợp lý mà tác nhân cần thực hiện. Đương nhiên là, khi ta thiết kế một tác nhân giải quyết một vấn đề nào đó thì CSTT sẽ chứa các tri thức về miền đối tượng cụ thể đó. Để máy tính có thể sử dụng được tri thức, có thể xử lý tri thức, chúng ta cần biểu diễn tri thức dưới dạng thuận tiện cho máy tính. Đó là mục tiêu của biểu diễn tri thức.

Tri thức được mô tả dưới dạng các câu trong ngôn ngữ biểu diễn tri thức. Mỗi câu có thể xem như sự mã hóa của một sự hiểu biết của chúng ta về thế giới hiện thực.

Ngôn ngữ biểu diễn tri thức (cũng như mọi ngôn ngữ hình thức khác) gồm hai thành phần cơ bản là cú pháp và ngữ nghĩa.

Cú pháp của một ngôn ngữ bao gồm các ký hiệu về các quy tắc liên kết các ký hiệu (các luật cú pháp) để tạo thành các câu (công thức) trong ngôn ngữ. Các câu ở đây là biểu diễn ngoài, cần phân biệt với biểu diễn bên trong máy tính. Các câu sẽ được

chuyển thành các cấu trúc dữ liệu thích hợp được cài đặt trong một vùng nhớ nào đó của máy tính, đó là biểu diễn bên trong. Bản thân các câu chưa chứa đựng một nội dung nào cả, chưa mang một ý nghĩa nào cả.

Ngữ nghĩa của ngôn ngữ cho phép ta xác định ý nghĩa của các câu trong một miền nào đó của thế giới hiện thực. Chẳng hạn, trong ngôn ngữ các biểu thức số học, dãy ký hiệu (x+y) *z là một câu viết đúng cú pháp. Ngữ nghĩa của ngôn ngữ này cho phép ta hiểu rằng, nếu x, y, z, ứng với các số nguyên, ký hiệu + ứng với phép toán cộng, còn * ứng với phép chia, thì biểu thức (x+y) *z biểu diễn quá trình tính toán: lấy số nguyên x cộng với số nguyên y, kết quả được nhân với số nguyên z.

Ngoài hai thành phần cú pháp và ngữ nghĩa, ngôn ngữ biểu diễn tri thức cần được cung cấp cơ chế suy diễn. Một luật suy diễn (rule of inference) cho phép ta suy ra một công thức từ một tập nào đó các công thức. Chẳng hạn, trong logic mệnh đề, luật modus ponens từ hai công thức A và AB suy ra công thức B. Chúng ta sẽ hiểu lập luận hoặc suy diễn là một quá trình áp dụng các luật suy diễn để từ các tri thức trong CSTT và các sự kiện ta nhận được các tri thức mới. Như vậy chúng ta xác định:

Ngôn ngữ biểu diễn tri thức = Cú pháp + Ngữ nghĩa + Cơ chế suy diễn

Một ngôn ngữ biểu diễn tri thức tốt cần phải có khả năng biểu diễn rộng, tức là có thể mô tả được mọi điều mà chúng ta muốn nói. Nó cần phải hiệu quả theo nghĩa là, để đi tới các kết luận, thủ tục suy diễn đòi hỏi ít thời gian tính toán và ít không gian nhớ. Người ta cũng mong muốn ngôn ngữ biểu diễn tri thức gần với ngôn ngữ tự nhiên.

Trước khi nghiên cứu logic vị từ - một ngôn ngữ biểu diễn tri thức có khả năng biểu diễn tương đối tốt, và hơn nữa nó là cơ sở cho nhiều ngôn ngữ biểu diễn tri thức khác, ta sẽ nghiên cứu logic mệnh đề. Logic mệnh đề là ngôn ngữ rất đơn giản, có khả năng biểu diễn hạn chế, song thuận tiện khi đưa vào nhiều khái niệm quan trọng trong logic.

3.2. Cú pháp và ngữ nghĩa của logic mệnh đề

Cú pháp của logic mệnh đề đơn giản, nó cho phép xây dựng nên các công thức. Cú pháp của logic mệnh đề bao gồm tập các ký hiệu và tập các luật xây dựng công thức.

3.2.1. Các ký hiệu

Hai hằng logic True và False.

Các ký hiệu mệnh đề (còn được gọi là các biến mệnh đề): P, Q,... Các kết nối logic , , , , .

Các dấu mở ngoặc (và đóng ngoặc).