Kiến trúc máy tính

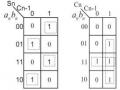
Số bit Khoảng giá trị

n bit: 0.. 2n - 1

8 bit 0.. 255 Byte

16 bit 0.. 65535 Word

Ví dụ 1.14:

Biểu diễn các số nguyên không dấu sau đây dùng 8 bit: A = 73 ; B = 138

Giải:

A = 73 = 64 + 8 + 1 = 26 + 23 + 20 = 0100 1001

B = 138 = 128 + 8 + 2 = 27 + 23 + 21 = 1000 1010

Ví dụ 1.15:

Hãy xác định giá trị của các số nguyên không dấu C, D được biểu diễn bằng 8 bit như sau:

C = 0010 1010; D = 1010 0110

Giải:

C = 0010 1010 = 25 + 23 + 21 = 32 + 8 + 2 = 42

D = 1010 0110 = 27 + 25 + 22 + 21 = 128 + 32 + 4 + 2 = 166

b) Biểu diễn số nguyên có dấu:

Phương pháp dùng dấu và độ lớn

Người ta sử dụng bit cao nhất biểu diễn dấu; bit dấu có giá trị 0 tương ứng với số nguyên dương, bit dấu có giá trị 1 biểu diễn số âm. Như vậy khoảng giá trị số được biểu diễn sẽ được tính như sau:

Số bit Khoảng giá trị:

n bit 2n-1-1

8 bit -128.. 127 Short integer

16 bit -32768.. 32767 Integer

32 bit -231.. 231-1 (-2147483648.. 2147483647) Long integer

Ví dụ 1.16:

Biểu diễn hai số +23 , -23 dùng phương pháp dấu và độ lớn.

Giải:

+23 = 0001 0111; -23 = 1001 0111

Vấn đề nảy sinh:

Cần quan tâm cả phần dấu và phần độ lớn khi thực hiện các phép toán số học Có đến 2 cách biểu diễn cho số 0 (+0 và -0)

Phương pháp dùng mã bù 2

Đối với số dương: biểu diễn dạng nhị phân

Đối với số âm: tìm số bù 2:

B1: đổi số dương tương ứng thành nhị phân B2: tìm số bù 1 (đảo bit 1 thành 0, 0 thành 1) B3: tìm số bù 2: số bù 1 cộng với 1

Số bù 2 thu được chính là cách biểu diễn số âm Đặc điểm:

Thực hiện các phép toán số học dễ dàng Chỉ có một sự biểu diễn duy nhất cho số 0 Ví dụ 1.17:

Biểu diễn các số nguyên có dấu sau đây bằng 8 bit: A = + 69; B = - 92.

Giải:

A = + 69 = 0100 0101 B = - 92

Ta có: + 92 = 0101 1100

Số bù 1 = 1010 0011

Số bù 2 = 1010 0100

Vậy: B = -92 = 1010 0100

Ví dụ 1.18:

Biểu diễn số nguyên có dấu A=+97 và B=-101 theo hai dạng kiểu n=8 bit và n=16 bit trong máy tính

Giải :

- Biểu diễn số A dạng số nguyên có dấu trong máy tính A = 0110 00012 (n=8 bit)

- Biểu diễn số B dạng số nguyên có dấu trong máy tính

Biểu diễn số +101 = 0110 01012

Lấy bù 2 1001 10112

=> B = - 101 = 1001 10112

- Biểu diễn số A dạng số nguyên có dấu trong máy tính A = 0000 0000 0110 00012 (n=16bit)

- Biểu diễn số B dạng số nguyên có dấu trong máy tính

Biểu diễn số +101 =0000 0000 0110 01012

Lấy bù 2 1111 1111 1001 10112

=> B = -101 = 1111 1111 1001 10112

1.5.4. Biểu diễn số thực

Có hai cách biểu diễn số thực trong một hệ nhị phân: số có dấu chấm cố định (fixed point number) và số có dấu chấm động (floating point number). Cách thứ nhất được dùng trong những bộ VXL (micro processor) hay những bộ vi điều khiển (micro

controller) cũ. Cách thứ 2 hay được dùng hiện nay có độ chính xác cao. Đối với cách biểu diễn số thực dấu chấm động có khả năng hiệu chỉnh theo giá trị của số thực. Cách biểu diễn chung cho mọi hệ đếm như sau:

R = m.Be

Trong đó m là phần định trị, trong hệ thập phân giá trị tuyệt đối của nó phải luôn nhỏ hơn 1. Số e là phần mũ và B là cơ số của hệ đếm.

Có hai chuẩn định dạng dấu chấm động quan trọng là: chuẩn MSBIN của Microsoft và chuẩn IEEE. Cả hai chuẩn này đều dùng hệ đếm nhị phân.

Thường dùng là theo tiêu chuẩn biểu diễn số thực của IEEE 754-1985(Institute of Electric & Electronic Engineers), là chuẩn được mọi hãng chấp nhận và được dùng trong bộ xử lý toán học của Intel. Bit dấu nằm tại vị trí cao nhất; kích thước phần mũ và khuôn dạng phần định trị thay đổi theo từng loại số thực.

Giá trị số thực IEEE được tính như sau:

Có 3 dạng:

Dạng đơn (single precision): 32 bit Dạng kép (double precision): 64 bit

Dạng kép mở rộng (double-extended precision): 80 bit

Dạng đơn

31 30 23 22

E (phần mũ)

M (phần định trị)

Có thể bạn quan tâm!

Xem toàn bộ 233 trang tài liệu này.

1bit

8 bit

23 bit

Hình 1. 21. Dạng đơn (single precision): 32 bit Khi đó, 1 số thực bất kỳ được biểu diễn:

X = (-1)S * 1,M * 2E – 127

Dải giá trị biểu diễn: 2-127< |X |< 2127,

hay: 10-38< |X |< 1038

Các bước thực hiện

- Bước 1: Đổi số thực đó  nhị phân

- Bước 2: Chuyển về dạng: 1,aa...a * 2b

- Bước 3: Xác định các giá trị:

+ S = 0 nếu số dương; S = 1 nếu số âm

+ E – 127 = b  E = 127 + b  nhị phân

+ M = aa...a00...0

Ví dụ 1.19:

Hãy biểu diễn số thực17,625 dưới dạng chuẩn IEEE 754/85 32 bit.

Giải :

- B1: A = 17,625 = 10001,101

- B2: A = 1,0001101 * 24 1,aa...a * 2b)

- B3: Ta có:

+ S = 0, vì A > 0

+ E – 127 = 4 E = 131 = 1000 0011

+ M = 000 1101 0000 0000 0000 0000

A = 0100 0001 1000 1101 0000 0000 0000 0000

= 41 8D 00 00H

Ví dụ 1.20:

Tìm giá trị số thực: C2 0D 00 00H

Giải:

Ta có: X = C2 0D 00 00H = 1100 0010 0000 1101 0000 0000 0000 0000

S = 1 X < 0

E = 1000 0100 = 132 E -127 = 5

M = 000 1101 0000 0000 0000 0000

X = -1,0001101 * 25 = -100011,01 = -35,25

Dạng kép

Khi đó, 1 số thực bất kỳ được biểu diễn: X = (-1)S * 1,M * 2E – 1023

Dải giá trị biểu diễn: 2-1023< |X |< 21023

hay: 10-308< |X |< 10308

63 62 52 50 0

E (phần mũ)

M (phần định trị)

1 bit

11 bit

52 bit

Hình 1. 22. Dạng kép (double precision): 64 bit

Dạng mở rộng

Khi đó, 1 số thực bất kỳ được biểu diễn: X = (-1)S * 1,M * 2E – 16383

Dải giá trị biểu diễn: 2-16383< |X |< 216383

Hay: 10-4932< |X|< 104932

79 78 64 63

E (phần mũ)

M (phần định trị )

1 bit

15 bit

64 bit

Hình 1. 23. Dạng kép mở rộng (double-extended precision): 80 bit

Cộng và trừ nhị phân:

- Phép cộng số học các số nhị phân được thực hiện theo quy tắc sau: 0 + 0 = 0

0 + 1 = 1 + 0 = 1

1 + 1 = 10,

Trong kết quả này số 0 được gọi là tổng (sum) số 1 được gọi là nhớ (carry). Phép cộng số học các số nhị phân nhiều bit được thực hiện theo quy tắc đó, áp dụng từ phải sang trái, carry từ phép cộng bit thấp được cộng thêm vào phép cộng ở bit cao hơn, carry của bit cao nhất là carry của cả phép cộng.

Ví dụ 1.21:

Thực hiện các phép tính cộng:

a) 1001 0110 b) 1100 1001

+ 0101 1011 + 0110 1101

Giải:

a) 1001 0110 b) 1100 1001

+0101 1011 + 0110 1101

1111 0001 10011 0110

Số 1 này là carry của phép cộng Người ta cần phải căn cứ vào quy tắc mã hoá số để so cách thức xử lý kết quả

thích hợp. Trong máy tính, bộ phận chứa kết quả cũng có độ dài (số bit) như là bộ phận chứa các toán hạng. Khi phép cộng cho kết quả có số bit vượt quá số bit của bộ phận thì kết quả của phép tính có thể không còn đúng nữa. Tuy nhiên, điều này lại còn phụ thuộc vào quy tắc mã hoá số.

Nếu các số hạng thực hiện phép cộng được mã hoá theo luật nhị phân tự nhiên thì số nhớ ra khỏi MSB (gọi là carry) báo hiệu có vấn đề ở kết quả tính. Xét hai ví dụ trên, ta thấy ở ví dụ a) phép cộng không có carry cho thấy kết quả của phép tính là bình thường (118 + 91 = 209), còn ở ví dụ b) carry của phép cộng cho thấy kết quả phép tính là không bình thường (201 + 109 = 54). Nếu các số hạng thực hiện phép cộng được mã hoá theo luật của số nguyên (ví dụ mã bù 2) thì ngay cả khi không có

carry, kết quả của phép tính cũng là không đáng tin nếu như có nhớ ở bit cao nhất của phần giá trị. Lại xét hai ví dụ trên, ta thấy ở ví dụ a) mặc dù không có carry nhưng kết quả của phép tính là không đúng (118 + 91 = -47). Còn ở ví dụ b) mặc dù phép cộng có carry nhưng kết quả của phép tính lại đúng (-55 + 109 = 54). Việc nhận xét kết quả phép cộng số nguyên phải dựa vào một dấu hiệu gọi là overflow, tức là trạng thái có một và chỉ một carry trong số hai bit tận cùng bên trái của kết quả (bit dấu và bit cao nhất của phần giá trị).

Nếu các số hạng được mã hóa theo BCD thì khi có nhớ ra khỏi một nhóm của một nhóm (một digit) hoặc giá trị một nhóm bốn bit lớn hơn 9 ta cần phải có sự hiệu chỉnh thích hợp, cụ thể là thêm 6 cho mỗi nhóm bốn bít đó.

Phép trừ các số nhị phân:

1 - 0 =1

0 - 0 =1-1 = 0

0-1=11

Trong kết quả (11) này,số 1 bên phải dược gọi là hiệu ,số1 bên trái là nhớ vay của phép trừ (gọi là carry hoặc borrow).

Ví dụ 1.22:

Trừ các số nhị phân nhiều bit sau:

1001 0110 0111 1001

- 0101 1011 - 1100 1101

Giải:

Phép trừ các số nhị phân nhiều bit được thực hiện như sau: 1001 0110 0111 1001

- 0101 1011 - 1100 1101

0011 1011 1 1010 1100

Số 1 này là carry/borrow của phép trừ Phép trừ số nhị phân cũng có thể được thưc hiện thông qua phép cộng: A-B = A+(-B)

Những lưu ý về tràn số và hiệu chỉnh kết quả phép tính đã trình bày ở phép cộng cũng được áp dụng đối với phép trừ.

Cộng số Hexa:

Khi cộng hai con số thập phân thì nếu tổng lớn hơn 9 ta viết con số đơn vị và nhớ con số hàng chục lên hàng cao kế. Tương tự khi cộng hai con số thập lục phân, nếu tổng lớn hơn F (tức 1510) ta viết con số đơn vị và nhớ con số hàng thập lục lên hàng cao kế.

Ví dụ 1.23:

Cộng các số Hexa sau:

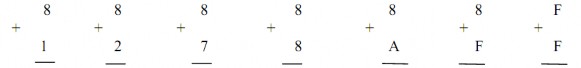
Giải:

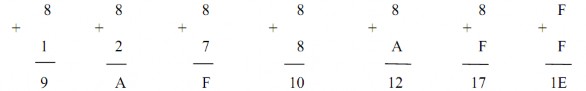
Trường hợp 8 + 8 = 1610 ta viết 16-16 = 0 và nhớ 1

Trường hợp 8 + A = 1810 ta viết 18-16 = 2 và nhớ 1

Trường hợp 8 + F = 2310 ta viết 23-16 = 7 và nhớ 1

Cùng qui luật trên áp dụng khi công hai số hex có nhiều con số, dĩ nhiên số nhớ cho hàng nào thì phải được cộng thêm vào cho hàng đó.

Ví dụ 1.24:

Cộng các số Hexa sau:

Giải:

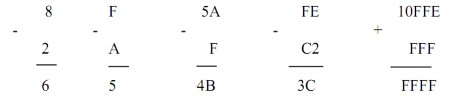
Trừ số Hexa:

Khi trừ hai số Hexa, nếu số trừ lớn hơn số bị trừ, ta mượn 1610 để thêm vào số bị trừ và trả 116 cho số trừ của hàng cao kế.

Ví dụ 1.25:

Trừ các số Hexa sau:

Giải:

Cộng các số BCD:

Cộng hai số BCD có điểm khác so với cộng hai số nhị phân bình thường. Khi tổng số ở mỗi số hạng của số BCD bằng 9 (=1001) hay nhỏ hơn thì tổng số đó là kết quả cuối cùng.

Ví dụ 1.26:

Cộng các số BCD sau:

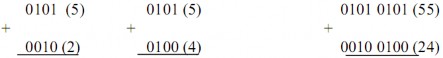
Giải:

Khi tổng số hai số nhị phân lớn hơn 9 tức từ 1001 trở lên thì tổng số không phải là số BCD nên phải cộng tổng số với 6 (0110) để có tổng số là 9 hoặc nhỏ hơn và tạo ra số nhớ 1 lên hàng BCD có nghĩa cao hơn.

Ví dụ 1.27:

Cộng các số BCD sau:

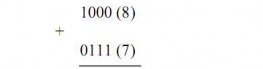
Giải:

Lý do cộng thêm 6 là vì mã BCD không dùng 6 mã cao nhất của số nhị phân 4 bit, có thể cộng nhiều hàng.

Ví dụ 1.28:

Cộng các số BCD sau:

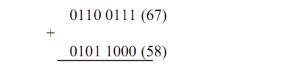
Giải: