Trang chủ / Học Sinh

Giáo án theo định hướng phát triển năng lực học sinh môn Đại số 10 - 25


BÀI TẬP

GỢI Ý


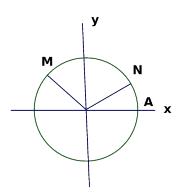
AM;

Cho cung AN.

- Hãy biểu diễn các cung đó trên đường tròn lương giác .

- Tìm tọa độ của các véc tơ OM ;ON.

- Tính tích vô hướng của hai véc tơ theo hai phương pháp .

- So sánh hai kết quả đó rồi đưa ra công thức.

ON  cos  sin  OM  cos  sin  ON OM  cos  cos   sin  sin  ON OM 1

ON (cos;sin )

OM (cos ;sin )

ON .OM cos.cos sin .sin


ON .OM ON .ON .cos(ON .OM )

Có thể bạn quan tâm!

Xem toàn bộ 217 trang tài liệu này.

+ Thực hiện: Học sinh hoạt động theo nhóm

+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức:

Trên cơ sở trả lời của học sinh, giáo viên chuẩn hóa lời giải, từ đó nêu công thức thứ nhất. Từ công thức đó hướng dẫn học sinh xây dựng công thức tính cos( + );sin(

- ); Sin( + ).Tính: tan( + ) ; tan( - ) theo tan , tan . HS viết nội dung công thức vào vở.

*Công thức cộng

cos(a b) cos a cos b sin a sin b cos(a b) cos a cos b sin a sin b sin( a b) sin a cos b sin b cos a

sin( a b) sin a cos b sin b cos a

tan( a b) tan a tan b

1 tan a tan b

tan( a b) tan a tan b

1 tan a tan b


Sản phẩm: Lời giải bài tập; học sinh biết được các công thức cộng.

2/ HĐ2:

- Mục tiêu: Học sinh hiểu công thức cộng và vận dụng công thức cộng vào giải các bài toán ở mức độ NB, TH, VD.

- Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh thảo luận nhóm theo bàn thực hiện giải các ví dụ sau.


VÍ DỤ

GỢI Ý


Ví dụ 1: Tính: cos 75, sin 75

.


cos 75 cos(45 30)

cos 45.cos 30 sin 45.sin 30

1 . 2 3 . 2 2 6

2 2 2 2 4

sin 75 cos 90 75 cos15

cos 45 30

cos 45.cos 30 sin 45.sin 30

2 . 3 2 . 1 6 2

2 2 2 2 4


Ví dụ 2: Tính

a) sin105

b) sin

12

a) sin105 sin 60 45

sin 60.cos 45 cos 60.sin 45

3 . 2 1 . 2 6 2

2 2 2 2 4

b) sin sin

12 3 4

sin .cos cos .sin

3 4 3 4

3 . 2 1 . 2 6 2

2 2 2 2 4


tan15, tan 5

Ví dụ 3: Tính 12

tan15 tan 45 30

tan 45 tan 30 1 3 1 tan 45. tan 30 1 3

tan 5 tan

12 4 6

tan tan 3 1

4 6

1 tan . tan 3 1

4 6

+ Thực hiện: Học sinh hoạt động theo nhóm theo bàn, viết lời giải ra giấy nháp. GV quan sát học sinh làm việc, nhắc nhở các em không tích cực, giải đáp nếu các em thắc mắc về nội dung ví dụ.


+ Báo cáo, thảo luận: Hết thời gian dự kiến cho từng ví dụ, quan sát thấy HS nào có lời giải tốt nhất thì gọi lên bảng trình bầy lời giải. Các HS khác quan sát lời giải, so sánh với lời giải của mình cho ý kiến.

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: GV chỉnh sửa, hoàn thiện lời giải trên bảng. Yêu cầu HS chép lời giải vào vở.

- Sản phẩm: Lời giải các ví dụ1, 2, 3. Học sinh biết phát hiện ra các bài toán dùng công thức cộng trong trường hợp đơn giản và áp dụng công thức để tìm ra đáp án. Biết các bước trình bày lời giải một bài toán áp dụng công thức cộng.


2.6.HTKT6: Công thức nhân đôi 1/ HĐ1:

- Mục tiêu: Tiếp cận và hình thành công thức nhân đôi.

- Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh nhận nhiệm vụ giải quyết bài tập sau.

CÂU HỎI

GỢI Ý

Câu1: Nêu công thức cộng. Câu2:

- Từ công thức cộng đối với sin và cos

nếu thay = thì công thức thay đổi ra sao ?

- tan cần điều kiện gì ?


- TínhCos2 ;sin2 ; tan2 ; Theo cos2 ?


Câu2: cos2 = cos2 -sin2 =2cos2 - 1 =1 - 2sin2

sin2= cos

2 tan

tan2 = 1 tan 2

(Với ; ) có nghĩa.

+ Thực hiện: Học sinh hoạt động theo nhóm

+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức:

Trên cơ sở trả lời của học sinh, giáo viên chuẩn hóa lời giải, từ đó nêu công thức nhân đôi và công thức hạ bậc. HS viết nội dung công thức vào vở.

*Công thức nhân đôi:


sin 2a 2sin a cos a

cos 2a cos2 a sin 2 a 2cos2 a 1 1 2sin 2 a

2 tan a

tan 2a

1 tan 2 a


Chú ý công thức hạ bậc:


cos2 a

1cos2a

2

sin2 a 1cos2a

2

tg2a 1cos2a

1cos2a

Sản phẩm: Lời giải bài tập; học sinh biết được các công thức nhân đôi và công thức hạ bậc.

2/ HĐ2:

- Mục tiêu: Học sinh hiểu công thức nhân đôi, công thức hạ bậc và vận dụng công thức đó vào giải các bài toán ở mức độ NB, TH, VD.

- Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh thảo luận nhóm theo bàn thực hiện giải các ví dụ sau.

VÍ DỤ

GỢI Ý


Ví dụ 1: Hãy tính theo cos .


cos4 = 8cos4 -8cos2 +1


Ví dụ 2: Tính .

1cos12

4 2 2 2

Ta có: cos2 8 = 2 = 2 = 4 .

2 2

cos 8 > 0 (vì 0 < 8 < 2 ).⇒ cos 8 = 2

.

Ví dụ 3: Đơn giản biểu thức :

sincoscos2

1 sin 4

4

+ Thực hiện: Học sinh hoạt động theo nhóm theo bàn, viết lời giải ra giấy nháp. GV quan sát học sinh làm việc, nhắc nhở các em không tích cực, giải đáp nếu các em thắc mắc về nội dung ví dụ.

+ Báo cáo, thảo luận: Hết thời gian dự kiến cho từng ví dụ, quan sát thấy HS nào có lời giải tốt nhất thì gọi lên bảng trình bầy lời giải. Các HS khác quan sát lời giải, so sánh với lời giải của mình cho ý kiến.

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: GV chỉnh sửa, hoàn thiện lời giải trên bảng. Yêu cầu HS chép lời giải vào vở.

- Sản phẩm: Lời giải các ví dụ1, 2, 3. Học sinh biết phát hiện ra các bài toán dùng công thức nhân đôi và công thức hạ bậc trong trường hợp đơn giản và áp dụng


công thức để tìm ra đáp án. Biết các bước trình bày lời giải một bài toán áp dụng công thức nhân đôi và công thức hạ bậc..


TIẾT 54


2.7.HTKT7: Công thức biến tổng thành tích và công thức biến tích thành tổng: 1/ HĐ1:

- Mục tiêu: Tiếp cận và hình thành công thức biến đổi tích thành tổng và tổng thành tích.

- Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh nhận nhiệm vụ giải quyết bài tập sau.

CÂU HỎI

GỢI Ý


Câu1:

1 cos cos

2

1cos cos

2

1 sin sin

2

Nêu công thức cộng.

Câu2: Từ các công thức biến đổi tích thành

x

tổng ở trên .Nếu đặt y

x y; x y

tứclà ( 2 2 )thì ta được các

công thức nào?


Câu1:

1cos cos

* 2 cos.cos

1cos cos

* 2 Sinsin

1sin sin

* 2 sincos

Câu2:

2cos x y cos x y

*cos x + cos y = 2 2 .

2sin x y sin x y

*cos x - cos y = 2 2

2sin x y cos x y

*sin x + siny = 2 2 .



2cos x y sin x y

*sin x - siny = 2 2

+ Thực hiện: Học sinh hoạt động theo nhóm

+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức:

Trên cơ sở trả lời của học sinh, giáo viên chuẩn hóa lời giải, từ đó biến đổi tích thành tổng và tổng thành tích.. HS viết nội dung công thức vào vở.

*Công thức biến đổi tích thành tổng :

cos a cos b 1 [cos(a b) cos(a b)]

2

sin a sin b 1 [cos(a b) cos(a b)]

2

sin a cos b 1 [sin(a b) sin(a b)]

2

*Công thức biến đổi tổng thành tích:

cos u cos v 2 cos uv cos uv

2

2

cos u cos v 2 sin uv sin uv

2

2

sin u sin v 2 sin u v cos u v

2

2

sin u sin v 2 cos uv sin uv

2

2


- Sản phẩm: Lời giải bài tập; học sinh biết được các công thức biến đổi tích

thành tổng và tổng thành tích .

2/ HĐ2:

- Mục tiêu: Học sinh hiểu công thức cộng và vận dụng công thức cộng vào giải các bài toán ở mức độ NB, TH, VD.

- Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh thảo luận nhóm theo bàn thực hiện giải các ví dụ sau.

VÍ DỤ

GỢI Ý

Ví dụ 1: Tính:

sin 5.sin

1. 24 24

Sử dụng công thức biến tích thành tổng

13 2

1. ĐS: 4


cos 7sin 5

2/ 12 12

1

2. ĐS: 4

Ví dụ 2: Chứng minh rằng

1/ 1 1 2 sin sin 3

10 10

2 / sin cos 2 sin

4

3 / sin cos 2 sin

4

Sử dụng công thức biến đổi tổng thành tích.

+ Thực hiện: Học sinh hoạt động theo nhóm theo bàn, viết lời giải ra giấy nháp. GV quan sát học sinh làm việc, nhắc nhở các em không tích cực, giải đáp nếu các em thắc mắc về nội dung ví dụ.

+ Báo cáo, thảo luận: Hết thời gian dự kiến cho từng ví dụ, quan sát thấy HS nào có lời giải tốt nhất thì gọi lên bảng trình bầy lời giải. Các HS khác quan sát lời giải, so sánh với lời giải của mình cho ý kiến.

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: GV chỉnh sửa, hoàn thiện lời giải trên bảng. Yêu cầu HS chép lời giải vào vở.

- Sản phẩm: Lời giải các ví dụ1, 2. Học sinh biết phát hiện ra các bài toán dùng công thức trên trong trường hợp đơn giản và áp dụng công thức để tìm ra đáp án. Biết các bước trình bày lời giải một bài toán áp dụng công thức trên.


2.8. Hoạt động luyện tập :

TIẾT 55

Kiểm tra bài cũ: Phát biểu các công thức: công thức cộng, công thức nhân đôi, công thứcbiến tổng thành tích và công thức biến tích thành tổng.

- Mục tiêu: Củng cố và vận dụng các công thức lượng giác đã học vào giải toán.

- Nội dung, phương thức tổ chức:

+ Chuyển giao:

Học sinh nhận nhiệm vụ giải quyết bài tập sau.


Vấn đề 1: Dấu của các giá trị lượng giác

Bài 1. Xác định dấu của các biểu thức sau:

a) A = sin500.cos(3000)


b) B =

sin2150.tan 21

7


cot 3.sin2

cos449

5

.sin .tan .cot

c) C =

3 d) D =

5 3 3 5


Bài 2. Cho

00 900 . Xét dấu của các biểu thức sau:


a) A = sin(900)

b) B =

cos(450)


c) C =

cos(2700 )

d) D =

cos(2900 )

Bài 3. Cho tam giác ABC. Xét dấu của các biểu thức sau:


a) A = sin AsinBsinC

cos A.cos B .cosC

b) B = sin A.sinB.sinC

tan A tan B tan C

c) C =

2 2 2 d) D =

2 2 2


Vấn đề 2: Tính các giá trị lượng giác của một góc (cung)

Bài 1. Tính các GTLG của các góc sau:

a) 1200; 1350; 1500; 2100; 2250; 2400; 3000; 3150; 3300; 3900; 4200; 4950; 25500

9; 11; 7; 13; 5; 10; 5; 11; 16; 13; 29; 31

b) 2 4 4 3 3 3 3 6 6 4

Bài 2. Cho biết một GTLG, tính các GTLG còn lại, với:

cosa 4 , 2700 a 3600

a)5

tan a 3, a 3

sin a

b)

5 ,

13 2

a

c)2

d) cot150 2

3

Bài 3.Cho biết một GTLG, tính giá trị của biểu thức, với:

A cot a tan a khi sin a 3 , 0 a

a) cot a tan a 5 2

sin2 a 2sin a.cosa 2cos2 a

C

b) 2sin2 a 3sin a.cosa 4cos2 a

sin a cosa 5


khi cot a 3

Bài 4. Cho 4 . Tính giá trị các biểu thức sau:


a) A sina.cosa

b) B sinacosa

c) C sin3 a cos3 a

+ Thực hiện: Học sinh hoạt động theo nhóm

+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời

+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Giáo viên nhận xét, chính xác hóa kết quả, rút kinh nghiệm và đánh giá.

..... Xem trang tiếp theo?
⇦ Trang trước - Trang tiếp theo ⇨

Ngày đăng: 01/03/2024