-Sản phẩm: Kết quả lời giải các bài tập trên. Củng cố và vận dụng được các công thức lượng giác đã học vào giải các bài tập trên. Rèn được tính cẩn thận trong giải toán.
TIẾT 56
- Mục tiêu: Củng cố và vận dụng các công thức lượng giác đã học vào giải toán.
- Nội dung, phương thức tổ chức:
+ Chuyển giao:
Học sinh nhận nhiệm vụ giải quyết bài tập sau.
HĐ GV và HS | |
1. Tính các GTLG của cung α nếu: 2 a) cosα = 3 và 2 3 b) tanα = 2 2 và2 2 32 c) sinα = 3 và 2 1 d) cosα = 4 và 2 2. Rút gọn biểu thức 2sin2sin4 a) A = 2sin2sin4 1cos2 b) B = tanα sin sin sinco s 4 4 sinco c) C = s 4 4 sin5sin3 d) D = 2cos4 3. Chứng minh đồng nhất thức 1cosx cos2x cot x a) sin2x sin x sinx sin x 2tan x 1cosx cosx 2 b) 2 | Học sinh làm việc cá nhân, hoạt động nhóm. |
Có thể bạn quan tâm!
-
Các Năng Lực Chính Hướng Tới Hình Thành Và Phát Triển Ở Học Sinh: -
Htkt2: Số Đo Của Cung Và Góc Lượng Giác: -
Giáo án theo định hướng phát triển năng lực học sinh môn Đại số 10 - 25
Xem toàn bộ 217 trang tài liệu này.
+ Thực hiện: Học sinh hoạt động theo nhóm
+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời
+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Giáo viên nhận xét, chính xác hóa kết quả, rút kinh nghiệm và đánh giá.
-Sản phẩm: Kết quả lời giải các bài tập trên. Củng cố và vận dụng được các công thức lượng giác đã học vào giải các bài tập trên. Rèn được tính cẩn thận trong giải toán.
Bài tập về nhà:
Bài 1: Chứng minh rằng :
1. cos( a + b)cos(a – b) = cos2a – sin2b
2. sina.sin( b – c) + sinb.sin( c- a) + sinc.sin( a – b) = 0
3. cosa.sin(b –c) + cosb.sin( c – a) + cosc.sin( a – b) = 0
4. cos( a + b)sin(a – b) + cos( b + c)sin(b –c ) + cos( c + a)sin( c – a) = 0
sin(a b)
5. cosa.cosb
sin(b c)
cosb.cosc
sin(c a) 0 cosc.cosa
sin4 a cos4 a
6.
sin6 a cos6 a
3 1 cos4a
4 4
5 3 cos4a
7. 8 8
tan2 2a tan2 a
8. 1 tan2 2a.tan2 a tan3a.tan a ;
(1
9.
1
cosa
)(1
1
cos2a
)(1
1
cos4a
)(1
1
cos8a
) tan8a.cot a
2
1
cosx.cos( x).cos( x) cos3x
10. 3 3 4
1
sin x.sin( x).sin( x) sin3x
11. 3 3 4
1 cosx cos2x cos3x 2cosx
12. 2cos2 x cosx 1
Bài 2: Chứng minh rằng các biểu thức sau không phụ thuộc vào biến số
A cos2 x cos2( 2x) cos2( 2
x)
1. 3 3
2. B = sin2(a + x) – sin2x – 2sinx.sina.cos( a + x) ( a là hằng số)
C sin2 x sin2(x 2) sin2(x 4)
3. 3 3
22
D tanx.tan(x ) tan(x ).tan(x ) tan(x
).tanx
4. 3 3 3 3
Bài 3: Chứng minh rằng :
21
23
45
cos .cos sin .sin sin .sin
1. 5 5 4 ; 2. 5 5 5 5 16
1 2 2 ... 2 2
2
1 2 2 ... 2 2
2
n1
n1
cos
3. 2
sin
;2
(n-dấu căn)
Bài 4: Không dùng máy tính hãy tính :
4
A cos .cos
1. 7 7
5
.cos
7
; 2.
B sin100.sin500.sin700
3. C sin60.sin420.sin660.sin780 4. sin180, cos180
Tiết 57
2.9. Hoạt động vận dụng :
- Mục tiêu: Củng cố và vận dụng các công thức lượng giác đã học vào giải toán bài toán liên môn trong vật lý.
- Nội dung, phương thức tổ chức:
+ Chuyển giao:
Học sinh nhận nhiệm vụ giải quyết bài toán sau.
HĐ GV và HS | |
Quỹ đạo một vật được ném lên từ gốc O, với vận tốc ban đầu v(m/s), theo phương hợp với ,0 trục hoành một góc 2 , là Parabol có y g x2 tanx phương trình 2v2 cos2 Trong đó g là gia tốc trọng trường ( g 9,8m / s2 )(giả sử lực cản của không khí không đáng kể). Gọi tầm xa của quỹ đạo là khoảng cách từ O đến giao điểm khác O của quỹ đạo với trục hoành. a) Tính tầm xa theo và v. b) Khi v không đổi, thay đổi trong 0; khoảng 2 , hỏi với giá trị nào thì tầm xa của quỹ đạo đạt giá trị lớn nhất? Tính giá trị lớn nhất đó theo v. Khi v=80m/s, hãy tính giá trị lớn nhất đó ( chính xác đến hàng đơn vị). | Học sinh làm việc cá nhân, theo nhóm |
+ Thực hiện: Học sinh hoạt động theo nhóm
+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời
+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Giáo viên nhận xét, chính xác hóa kết quả, rút kinh nghiệm và đánh giá.
- Sản phẩm Củng cố và vận dụng các công thức lượng giác đã học vào giải toán bài toán liên môn trong vật lý. Rèn được tính cẩn thận trong giải toán.
2.10. Hoạt động tìm tòi mở rộng :
- Mục tiêu: Bước đầu giúp học sinh tìm hiểu và thực hành sử dụng giá trị lượng giác, công thức lượng giác...vào việc đo đạc, bài toán thực tê.
- Nội dung, phương thức tổ chức:
+ Chuyển giao:
Học sinh nhận nhiệm vụ giải quyết bài toán sau.
HĐ GV và HS | |
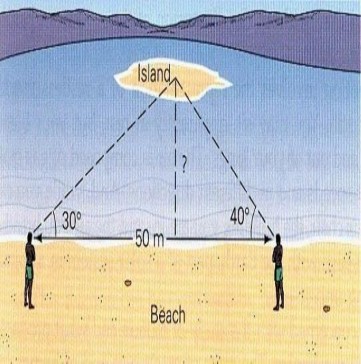
Giả sử đang ở bãi biển và thấy một hòn đảo. Nhưng chúng ta lại không biết khoảng cách từ bờ biển đến đảo có xa không ? Vậy làm sao có thể tính được khoảng cách đó mà không đến hòn đảo? Giáo viên định hướng cho học sinh 1 cách đo với các số liệu như trong hình. Từ đó sử dụng giá trị lượng giác của góc để giải bài toán. Gọi x là khoảng cách cần tìm, ta có phương trình : 50 x cot 400 x cot 300 Từ đó ta dễ dàng tìm được khoảng cách x. |
|
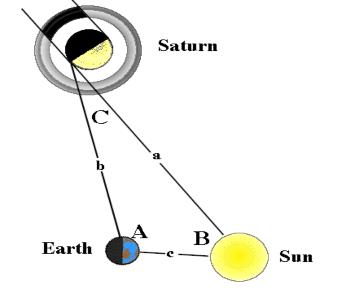
Trong thiên văn người ta có thể sử dụng giá trị lượng giác, công thức lượng giac… để đo khoảng cách giữa các hành tình với nhau. |
|
+ Thực hiện: Học sinh hoạt động theo nhóm
+ Báo cáo, thảo luận: Cho học sinh đại diện nhóm trả lời
+ Đánh giá, nhận xét, tổng hợp chốt kiến thức: Giáo viên nhận xét, chính xác hóa kết quả, rút kinh nghiệm và đánh giá.
- Sản phẩm : Các báo cáo các kết quả đo đạc của các nhóm.