Phương Pháp Học Tập Phục Vụ Cộng Đồng (Service Learning)

dàng, sâu và nhớ lâu hơn các phương pháp giảng dạy truyền thống (Scholz và Olaf, 2002). Phương pháp này có thể giúp đạt được CĐR theo đề cương CDIO như: Đề ra các giải pháp; Ước lượng và phân tích định tính.

10.2.4. Phương pháp học tập phục vụ cộng đồng (Service Learning)

Học tập phục vụ cộng đồng (tên tiếng Anh là Service Learning hoặc Community-based learning) đã có từ năm những năm 1960 tại Mỹ (Jacoby,1996). Service-Learning (SL) là một phương pháp dạy và học mà thông qua đó người học áp dụng được những kiến thức học được trong lớp vào điều kiện thực tế, đồng thời kết quả của quá trình học đáp ứng nhu cầu của cộng đồng và được cộng đồng sử dụng. SL đã được áp dụng tại nhiều trường ĐH trên khắp thế giới, đến nay tại Hoa Kỳ đã hơn 1.000 trường ĐH và Cao đẳng áp dụng phương pháp này cho hơn 6 triệu sinh viên (Campus Compact, 2007). SL được xem là một chiến lược phát triển bền vững của các trường ĐH tại Hoa Kỳ và đang dần dần ảnh hưởng sang các trường ĐH khác tại châu Á. Phương pháp SL là một sự phối hợp làm việc, hợp tác trên cơ sở các mối quan hệ của 4 thành phần tham gia là: nhà quản lý trường học (Administrator), giảng viên (Faculty), cộng đồng (Community Partner) và sinh viên (Student). Ưu điểm của SL là giúp người học làm phong phú kiến thức của mình từ lý thuyết đến thực tế và ngược lại (bring books to life and life to books), quá trình học này thông qua trải nghiệm nên người học có điều kiện tăng cường kiến thức học thuật, rèn luyện và phát triển các kỹ năng mềm như tư duy suy xét, phản biện (critical thinking), làm việc theo nhóm, giao tiếp, thuyết trình và các kỹ năng sống (Hình 3).

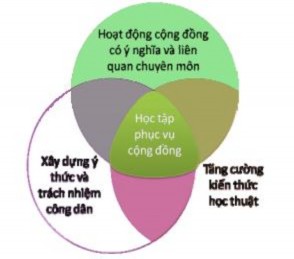
Hình 3. Học tập phục vụ cộng đồng trong mối quan hệ giữa hoạt động học và phục vụ Phương pháp học tập phục vụ cộng đồng được thực hiện theo các bước như sau: (1)

Cộng đồng nêu vấn đề cần giải quyết; (2) Giáo viên lồng ghép các vấn đề cộng đồng cần

giải quyết vào môn học như là đề tài thực tập của sinh viên. Điều quan trọng cần lưu ý là các đề tài này phải phù hợp với nội dung môn học, trình độ và kỹ năng của sinh viên; (3) Sinh viên được tổ chức thành nhóm thực hiện đề tài dưới sự hướng dẫn của giáo viên. Khi thực hiện đề tài, sinh viên phải vận dụng các kiến thức của môn học để cùng cộng đồng giải quyết các vấn đề; (4) Kết quả của đề tài được cộng đồng sử dụng . Phương pháp này có thể giúp đạt được CĐR theo đề cương CDIO như: Vai trò và trách nhiệm đối với xã hội; Nhận biết được bối cảnh các tổ chức xã hội; Ham tìm hiểu và học tập suốt đời, Tư duy suy xét; Làm việc nhóm; Kỹ năng giao tiếp bằng văn viết và thuyết trình.

PHỤ LỤC 11 GIÁO ÁN

K VỌNG TOÁN CỦA BIẾN NGẪU NHIÊN RỜI RẠC

Bước 1: Xác định chuẩn đầu ra bài học

Dạy học theo tiếp cận CDIO có nghĩa là dạy học đáp ứng yêu cầu nghề nghiệp của người học. Vì vậy đối với mỗi nội dung kiến thức giảng dạy người GV cần xác định ứng dụng của nội dung kiến thức đối với thực ti n nghề và hướng dẫn cho SV ứng dụng kiến thức vào giải quyết tình huống nghề nghiệp trong bài giảng. Bên cạnh việc dạy học đáp ứng yêu cầu về kiến thức và ứng dụng của kiến thức đối với nghề nghiệp, thì dạy học theo CDIO đòi hỏi người học đạt yêu cầu về kỹ năng nghề nghiệp, do đó đối với mỗi bài dạy người GV cần xác định yêu cầu CĐR cụ thể về kiến thức và kĩ năng thông qua mỗi nội dung dạy học. Hơn nữa, để người GV được thuận lợi trong dạy học thì bài giảng cần cho biết cơ hội hình thành và rèn luyện kỹ năng nghề nghiệp thông qua các phần của bài giảng một cách cụ thể.

Đối với bài học “Kỳ vọng toán của biến ngẫu nhiên” thì cần làm sáng tỏ cho SV về ý nghĩa và ứng dụng kì vọng trong kinh tế: Đánh giá lợi nhuận của dự án đầu tư, chi phí bảo hiểm chấp nhận được, phí bảo hiểm đề xuất để có lợi nhuận,….. Bài dạy cần hướng đến hình thành và rèn luyện các KNNN cho SV: mô hình hóa, sử dụng ngôn ngữ toán học, giải quyết vấn đề…. Từ nội dung, mục đích, yêu cầu của bài giảng chúng tôi xác định CĐR bài dạy về: Kiến thức, kĩ năng, cơ hội hình thành kĩ năng cho SV trong bài giảng, thái độ như sau.

Sản phẩm của phần này là mục A có cấu trúc sau đây.

Kiến thức

Kĩ năng

Cơ hội hình thành

Thái độ

CĐR BÀI HỌC

A. Chuẩn đầu ra bài học

1. Về kiến thức

- Nắm được khái niệm kỳ vọng toán của biến ngẫu nhiên rời rạc, các tính chất của kỳ vọng toán của biến ngẫu nhiên, ý nghĩa của kỳ vọng toán trong môn XSTK, ứng dụng của kỳ vọng toán trong nghề kinh tế.

2. Về kĩ năng

- Tính thành thạo kỳ vọng toán của các biến ngẫu nhiên.

- Giải thích ý nghĩa số phản ánh giá trị trung bình cho các bài toán chứa đựng các yếu tố liên quan đến thực ti n nghề kinh tế về biến ngẫu nhiên.

- Có kĩ năng đặt và giải quyết các bài toán đặt ra trong thực ti n nghề, đặc biệt là các bài toán về thực ti n của nghề kinh tế bằng vận dụng các kiến thức về kỳ vọng toán của biến ngẫu nhiên.

- Có kĩ năng hoạt động nhóm để giải quyết các bài toán thực ti n nghề kinh tế có sử dụng kiến thức kỳ vọng toán.

- Có kĩ năng mô hình hóa bài toán kinh tế.

3. Cơ hội hình thành và rèn luyện KN cho SV trong bài giảng

STT

TÊN KỸ

NĂNG

M TẢ THỰC HIỆN TRONG BÀI HỌC

SỐ LẦN

Mô hình hóa

SV được GV hướng dẫn các bước mô hình hóa một

bài toán thực ti n kinh tế thông qua bài toán mở đầu và các bài tập ứng dụng của kì vọng.

Giải quyết vấn đề

Trong quá trình giải quyết bài toán mở đầu, bài tập áp dụng của kì vọng, SV sẽ gặp các vấn đề chưa có cách thức và trình tự giải quyết. SV sẽ từng bước khắc phục

khó khăn để giải quyết.

Sử dụng ngôn

ngữ toán học

Sử dụng kì vọng và các tham số trong giải quyết bài

toán kinh tế.

Làm việc

nhóm

Trao đổi theo nhóm để đưa ra câu trả lời trong phiếu.

Tư duy sáng

tạo

Trả lời câu hỏi trong phiếu từ những gợi ý của bài toán

và đưa ra công thức tính kì vọng.

Tư duy phản

biện

Trao đổi từng cặp hoặc theo nhóm để thống nhất các

câu trả lời

Có thể bạn quan tâm!

Xem toàn bộ 245 trang tài liệu này.

4. Về thái độ

- SV ý thức được việc học tập để phục vụ cho việc học các môn chuyên ngành, phục vụ cho thực ti n và hoạt động nghề khối kinh tế.

Bước 2. Tích hợp CĐR bài học, môn học và chương trình theo CDIO

Ý nghĩa của dạy học theo tiếp cận CDIO là nhằm đáp ứng CĐR, để thể hiện điều này thì GV cần tích hợp CĐR bài học vào CĐR môn học và CĐR CTĐT. Đây là bước tiếp theo và là bắt buột của dạy học theo tiếp cận CDIO, nó cho thấy việc dạy học các bài học trong môn học góp phần đáp ứng CĐR của môn học và của CTĐT một cách rõ ràng và khoa học.

Sản phẩm của bước này là mục B sau đây

B. Tích hợp chuẩn đầu ra

CĐR

NỘI DUNG CĐR	CĐR MÔN HỌC	CĐR CTĐT CDIO
KIẾN THỨC	Nắm được khái niệm kỳ vọng toán của biến ngẫu nhiên rời rạc	G1.2	1.2
	Nêu được các tính chất của kỳ vọng toán của biến ngẫu nhiên	G1.2	1.2
	Biết được ý nghĩa của kỳ vọng toán trong môn XSTK	G1.2	1.2
	Hiểu ứng dụng của kỳ vọng toán trong nghề kinh tế	G1.2	1.2
KỸ NĂNG	Tính thành thạo kỳ vọng toán của biến ngẫu nhiên	G2.4	2.1
	Mô hình hóa bài toán ứng dụng kỳ vọng trong kinh tế	G2.9	2.1
	Vận dụng kỳ vọng giải quyết bài toán ứng dụng trong kinh tế	G2.9	2.2
	Sử dụng ngôn ngữ toán học	G2.4	2.1
	Làm việc nhóm	G3.2	3.1
	Tư duy sáng tạo	G2.10	2.4.7
	Tư duy phản biện	G2.10	2.4.8
THÁI ĐỘ	Ý thức được việc học tập để phục vụ cho việc học các môn chuyên ngành, phục vụ cho thực ti n và hoạt động nghề khối kinh tế	G3.1	2.5

Bước 3. Thiết kế bài dạy theo mô hình dạy học trải nghiệm CDIO

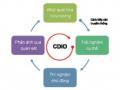
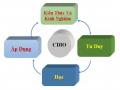
Dạy học theo tiếp cận CDIO đòi hỏi SV đạt được các yêu cầu về kiến thức và kỹ năng đã đặt ra trong CĐR mỗi bài dạy cụ thể. Vì vậy bài dạy cần được thiết kế theo mô hình dạy học trải nghiệm của CDIO gồm 4 bước như sau.

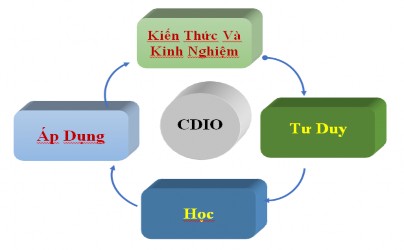
Các bước của quá trình này được vận dụng một cách linh hoạt vào các phần dạy của bài học. Trong thực hiện các bước của mô hình cần sử dụng kết hợp các biện pháp sư phạm đã đề xuất và các phương pháp dạy học chủ động trải nghiệm nhằm giúp SV có cơ hội trải nghiệm nghề nghiệp và đạt các yêu cầu của CĐR về kiến thức và kỹ năng.

Sản phẩm của bước này là mục C sau đây.

C. Bài giảng theo mô hình trải nghiệm CDIO

1. Nhiệm vụ và yêu cầu đối với GV, SV

Nội dung

Thời lượng

Nhiệm vụ GV

Nhiệm vụ SV

Phương tiện

Hiệu quả đối với SV

Kỳ vọng

toán của biến ngẫu nhiên rời rạc

2 tiết

+Thiết kế bài giảng theo mô hình dạy học trải nghiệm CDIO.

+Chiếu các slide và đặc vấn đề.

+Đặt câu hỏi.

+Giảng ít.

+Dẫn dắt SV vào trọng tâm.

+Viết bảng trắng.

+Xem slide và suy nghĩ.

+Nghe giảng ít.

+Tham gia vào các vấn đề GV nêu ra.

+Lên bảng.

+Thảo luận nhóm.

+Máy vi tính

+Máy chiếu Projector, Powerpoint.

+Các slide bảng cố định, bảng trắng.

+Hình ảnh d tiếp thu.

+D theo dõi bài.

+Chủ động chiếm lĩnh tri thức theo trình

tự chu trình học trải nghiệm CDIO.

+Giờ học

sinh động, chủ động thảo luận nhóm.

+Tự kết luận.

2. Tiến trình bài giảng

Bài giảng được thiết kế sử dụng mô hình dạy học trải nghiệm CDIO, gồm 4 bước, được vận dụng linh hoạt trong các nội dung giảng dạy. Bài giảng sử dụng kết hợp các kỹ thuật của những biện pháp sư phạm và các phương pháp giảng dạy tích cực chủ động theo đề xuất CDIO nhằm giúp SV đạt các CĐR về kiến thức và kỹ năng đặt ra.

Hoạt động của GV

Mục đích, vai trò

của SV

Biện pháp –

phương pháp

Chiếu slide 1

BÀI TOÁN MỞ ĐẦU

Trong một cuộc xổ số được tiến hành để giúp quỹ từ thiện địa phương,

10.000 vé số sẽ được bán với giá 5USD mỗi vé. Giải thưởng là một chiếc xe ôtô trị giá 12.000USD. Nếu anh/chị mua hai vé số, thì khoản lợi kỳ vọng của anh/chị là bao nhiêu?

? GV yêu cầu SV nhớ lại bảng phân phối XS của ĐLNN.

? Cách tính giá trị trung bình số học.

Quá trình 1: Kiến thức và kinh nghiệm

+Thầy nêu bài toán mở đầu

+Trò nghe

+Tái hiện lại các kiến thức đã học, đã từng sử dụng

-Kỹ thuật 2.1 – Biện pháp 2

-Dạy học dựa trên vấn đề

Chiếu Slide 2

GV đặt các câu hỏi?

1. Gọi X là khoản lợi có thể nhận, X có thể nhận những giá trị nào?

2. Xác suất tương ứng với mỗi giá trị X nhận là bao nhiêu?

3. Hãy lập bảng phân phối xác suất của X?

4. Giá trị trung bình của X là bao nhiêu? Tính như thế nào?

5. Các em có bao giờ tính giá trị trung bình chưa? Trong trường hợp nào?

6. Trường hợp bài toán có sử dụng được công thức đó hay không? Tại sao? Giống và khác nhau giữa trung

bình số học và trung bình ĐLNN?

Quá trình 2: Tư duy

+SV suy nghĩ 5 phút và trả lời câu hỏi GV đặt ra.

+SV trao đổi từng cặp hoặc theo nhóm nhỏ (theo bàn).

+Hoàn thành và nộp phiếu hỏi cho GV.

-Kỹ thuật 2.2,

2.3–Biện pháp 2

-Động não - Suy nghĩ từng cặp - chia sẽ

X
P(X)

	7. Tổng xác suất của một đại lượng ngẫu nhiên luôn bằng bao nhiêu? 8. Nêu công thức tính trung bình của ĐLNN như thế nào? 9. Kết luận lợi nhuận kì vọng? b/ Phát phiếu cho nhóm (5SV/nhóm, 8 nhóm/lớp) Mẫu phiếu: KỲ VỌNG ĐLNN 1/ Gọi X là lợi nhuận, bảng phân phối XS của X là: 2/ Lãi kỳ vọng: …………………….
3	3	Chiếu slide 3 GV tổng kết câu trả lời Nêu công thức tính kì vọng của ĐLNN. Đặt thêm câu hỏi thảo luận: Lợi nhuận kì vọng là bao nhiêu nếu chúng ta mua 3 vé? Liệu có lỗ hay không?	Quá trình 3: Học +SV đưa ra kết quả bài toán và kết luận. +Trình bày công thức tính kỳ vọng của ĐLNN. +GV tổng kết.	-Hoạt động nhóm
4	4	GV chiếu slide 4 Áp dụng 1: Một công ty bảo hiểm bán thẻ bảo hiểm với giá 100 nghìn đồng/ 1người/ 1năm. Nếu người tham gia bảo hiểm gặp rủi ro trong năm đó thì nhận được số tiền bồi thường là 1 triệu đồng. Theo thống kê biết rằng tỷ lệ người tham gia bảo hiểm bị rủi ro trong năm là 0,05. Hãy tính tiền lãi trung bình khi bán mỗi thẻ bảo hiểm?	Quá trình 4: Áp dụng +Một SV lên bảng lập bảng phân phối của số tiền lãi. +Một SV khác tính kì vọng và kết luận.	- Kỹ thuật 3.1, 3.2, 3.4, 3.5 – Biện pháp 3
5	5	GV chiếu slide 5 Áp dụng 2 (vận dụng cao): Hãy xác định phí bảo hiểm hàng năm cho một hợp đồng bảo hiểm có giá trị 1000USD và bảo hiểm một biến cố đã xảy ra với tỷ lệ 2 lần trong 100, trong suốt một thời kỳ dài. Gọi X bằng khoản lợi tài chính hàng năm của công ty bảo hiểm do việc bán hợp đồng bảo hiểm này, và gọi C bằng mức phí bảo hiểm hàng năm chưa biết. Tính giá trị của C sao cho khoản lợi kỳ vọng, E(X), sẽ bằng 0?	Quá trình 1 +SV tái hiện kiến thức vừa học. +Suy nghĩ cách áp dụng vào bài toán này.