Dạy học kĩ thuật lập trình cho sinh viên ngành Kĩ thuật điện tử - viễn thông theo hướng phát triển tư duy điện toán

Minh họa cho bài toán nội suy được ứng dụng trong thực tế như việc phóng to, thu nhỏ ảnh, các ứng dụng về chương trình thời tiết, hoặc ứng dụng trong sinh học về việc phân tích quần thể về các trường hợp mắc bệnh truyền nhiễm bệnh trong xã hội, xây dựng bản đồ hiện trạng chất lượng không khí,…

c4. Thuật toán xấp xỉ tích phân

Các phương pháp Monte Carlo [10] là một lớp các thuật toán để giải quyết nhiều bài toán trên máy tính theo kiểu không tất định, thường bằng cách sử dụng các số ngẫu nhiên (thường là các số giả ngẫu nhiên), ngược lại với các thuật toán tất định. Một ứng dụng cổ điển của phương pháp này là việc tính tích phân xác định, đặc biệt là các tích phân nhiều chiều với các điều kiện biên phức tạp.

Các phương pháp này đặc biệt hiệu quả khi giải quyết các phương trình vi-tích phân; ví dụ như trong mô tả trường bức xạ hay trường ánh sáng trong mô phỏng hình ảnh ba chiều trên máy tính, có ứng dụng trong trò chơi điện tử, kiến trúc, thiết kế, phim tạo từ máy tính, các hiệu ứng đặc biệt trong điện ảnh, hay trong nghiên cứu khí quyển, và các ứng dụng nghiên cứu vật liệu bằng laser...

Trong toán học, thuật toán Monte Carlo là phương pháp tính bằng số hiệu quả cho nhiều bài toán liên quan đến nhiều biến số mà không dễ dàng giải được bằng các thuật toán khác, chẳng hạn bằng tính tích phân. Hiệu của của phương pháp này, so với các phương pháp khác, tăng lên khi số chiều của bài toán tăng. Monte-Carlo cũng được ứng dụng cho nhiều lớp bài toán tối ưu hóa.

Trong các hệ thống truyền thông số phức tạp, tốc độ lỗi bit (BER) là thông số quan trọng nhất trong việc đánh giá hiệu suất của hệ thống. Thuật toán Monte Carlo trở thành công cụ mô phỏng hiệu quả các thông số này. Các hệ thống ngày nay hoạt động trong các môi trường được đặc trưng bởi nhiễu, sự không tuyến tính, tính đa đường và hàng loạt ảnh hưởng khác. Do vậy, mô phỏng Monte Carlo trở thành một phương pháp khả thi [10] [11].

Một số đoạn chương trình mô phỏng thuật toán Monte Carlo như:

Có thể bạn quan tâm!

Xem toàn bộ 235 trang tài liệu này.

# Tinh gan dung tich phan tren [a,b] x [c,d] - Ve hinh tron

import numpy as np

import matplotlib.pyplot as plt

import time

def hamf(x,y):

f = (1+(1-x)**2 + 10*(y-x**2)**2)

return f a,b = 0,1

c,d = 0,1

# Start time

Start = time.time() N = 5000

X = np.random.uniform(a,b,N) Y = np.random.uniform(c,d,N) Xc = [ ]

Yc = [ ]

for i in range(N):

r2 = (X[i]-0.5)**2 + (Y[i]-0.5)**2

if r2 <= 0.25:

Xc = np.append(Xc,X[i]) Yc = np.append(Yc,Y[i])

fX = hamf(Xc,Yc) N2 = Xc.shape[0]

Imc = np.pi*0.25**2*np.sum(fX)/N2

# End time

End = time.time()

Total = End - Start print("Approximated Value is : ", Imc)

print("Elapsed wall-clock time is : ", Total) plt.plot(Xc,Yc,'b.')

plt.xlabel('X-direction') plt.ylabel('Y-direction') plt.show()

# Tinh gan dung tich phan tren [a,b] x [c,d] – Ve HCN

import numpy as np

import matplotlib.pyplot as plt

def hamf(x,y):

f = (1+(1-x)**2 + 10*(y-x**2)**2)

return f a,b = 1,2

c,d = 0,1

N = 5000

X = np.random.uniform(a,b,N) Y = np.random.uniform(c,d,N) fXY = hamf(X,Y)

Imc = (b-a)*(d-c)*np.sum(fXY)/N

print("Gia tri tich phan gan dung la : ", Imc)

Bên cạnh đó, GV cần cho SV sử dụng tư duy điện toán để phân tích thuật toán Monte Carlo khi ứng dụng trong thực tế ngày nay. Phương pháp Monte Carlo có thể áp dụng cho tất cả các hệ thống mà không cần quan tâm tới kiến trúc hay độ phức tạp, nhưng có một trở ngại quan trọng. Vấn đề cơ bản với phương pháp Monte Carlo đó là thời gian cần để thực hiện một mô phỏng và đạt được một ước lượng đáng tin cậy về hiệu suất của hệ thống thường rất dài. Đặc biệt, trong hầu hết các hệ thống truyền thông số phức tạp trong thực tế với nhiễu ngẫu nhiên và sự không tuyến tính, không thể tính được chính xác xác suất lỗi bằng cách phân tích. Việc ước lượng các sự kiện có xác suất lỗi thấp, hay các sự kiện hiếm bằng cách sử dụng trực tiếp các kĩ thuật mô phỏng Monte Carlo cổ điển thường đòi hỏi số lần thực hiện rất lớn. Từ những hạn chế của kĩ thuật Monte Carlo cổ điển, cần tìm ra một phương

pháp để có thể mô phỏng những hệ thống có xác suất lỗi thấp, đồng thời đảm bảo thời gian thực hiện ngắn. Một phương pháp dựa trên kĩ thuật Monte Carlo đã chỉnh sửa, gọi là kĩ thuật lấy mẫu theo trọng số (IS) được nghiên cứu và sử dụng. IS là kĩ thuật có khả năng cải thiện thời gian chạy mô phỏng trên máy tính, và cung cấp một ước lượng BER thu được có phương sai nhỏ hơn ước lượng theo kĩ thuật Monte Carlo có thời gian mô phỏng tương đương. Kĩ thuật IS đã được áp dụng trong rất nhiều lĩnh vực, như truyền thông sợi quang, vệ tinh, các kênh không tuyến tính và không có dạng Gauss, ước lượng hiệu suất của các hệ thống tính toán có độ tin cậy cao, lý thuyết xếp hàng, thuật toán dò,…

c5. Mô hình hoá và mô phỏng

Mô hình hóa là một quá trình thay thế hệ thống thực bằng một mô hình để nhằm thu nhận các thông tin của hệ thống bằng cách tiến hành các thực nghiệm, tính toán trên mô hình .

Mặc dù chỉ có thể xây dựng được mô hình gần đúng với hệ thống thực, mô hình hóa luôn luôn là một phương pháp hữu hiệu để con người nghiên cứu hệ thống, nhận biết các quá trình, các quy luật tự nhiên. Đặc biệt, ngày nay nhờ có sự trợ giúp đắc lực của máy tính, có thể phát triển các phương pháp mô hình hóa cho phép xây dựng các mô hình ngày càng gần với hệ thống nghiên cứu, đồng thời việc thu nhận lựa chọn, xử lý các thông tin về mô hình rất thuận tiện, nhanh chóng và chính xác. Chính vì vậy, mô hình hóa là một phương pháp nghiên cứu khoa học giúp cho SV luyện tập tư duy điện toán, phân tích bài toán và có thể ứng dụng vào thực tiễn.

Mô phỏng là phương pháp mô hình hóa dựa trên việc xây dựng mô hình số và dùng phương pháp số để tìm các lời giải. Chính vì vậy, máy tính số là công cụ duy nhất và hữu hiệu để thực hiện việc mô phỏng hệ thống. Mô hình số được xây dựng dựa trên phương pháp số tức là bằng các chương trình

chạy trên máy tính số. Mô phỏng bằng máy tính: Xây dựng và thử nghiệm các mô hình thực tế của một hệ thống trên một máy tính [2].

Mô hình hóa toán học là quá trình chuyển đổi từ vấn đề thực tế sang vấn đề toán học bằng cách thiết lập và giải quyết các mô hình toán học. Cụ thể, mô hình hóa toán học là toàn bộ quá trình chuyển đổi từ vấn đề thực tiễn sang vấn đề toán học và ngược lại, cùng với các yếu tố liên quan đến quá trình đó như: từ bước xây dựng lại tình huống thực tiễn, lựa chọn mô hình toán học phù hợp, làm việc trong một môi trường toán học, giải thích, đánh giá kết quả liên quan đến tình huống thực tiễn và điều chỉnh mô hình cho đến khi có được kết quả hợp lí [9].

Về mặt nhận thức, mô hình là sản phẩm của quá trình tư duy, ra đời nhờ quá trình trừu tượng hóa các đối tượng cụ thể. Trong quá trình trừu tượng hóa, cần loại bỏ dấu hiệu không bản chất, chỉ giữ lại những thuộc tính bản chất.

Mô hình hóa trong dạy học Toán là quá trình giúp SV tìm hiểu, khám phá các tình huống nảy sinh từ thực tiễn bằng công cụ và ngôn ngữ Toán học với sự hỗ trợ của công nghệ thông tin. Quá trình này đòi hỏi SV cần có các kĩ năng và thao tác tư duy Toán học như phân tích, tổng hợp, so sánh, khái quát hóa, trừu tượng hóa. Điều này SV cần phải có quá trình rèn luyện tư duy điện toán để hình thành kỹ năng xử lý. GV tiến hành dạy cho SV mô hình hóa gắn chặt với tư duy điện toán [10].

Chẳng hạn có một ứng dụng trong sinh học mô phỏng cách tư duy mô hình hóa một bài toán trong thực tế [44]. Đó là muốn đo sự thay đổi dân số trong quần thể (Hình 2.1) theo thời điểm t.

Bài toán được phát biểu tóm lược như sau:

Ta gọi N(t) là tổng số dân tại thời điểm t, trong đó:

- Số người khoẻ mạnh (chưa bị nhiễm bệnh) là S(t);

- Số người bắt đầu nhiễm bệnh nhưng chưa truyền nhiễm cho người khác là E(t);

- Số người bị nhiễm bệnh và truyền nhiễm cho người khác là I(t);

- Số người đã khỏi bệnh và miễn dịch với bệnh là R(t). Như vậy, N(t) = S(t) + E(t) + I(t) + R(t)

Hãy mô hình hoá và nghiên cứu mô phỏng về sự truyền nhiễm bệnh giữa các nhóm đối tượng nêu trên trong quần thể.

GV hướng dẫn SV cách tư duy về bài toán sao cho tìm ra thuật toán đưa về công thức tính toán cụ thể, tức là muốn đo dân số tại thời điểm t bằng cách lấy dân số thời gian sau – dân số thời gian trước.

- Hàm S(t): tăng do dân số sinh tự nhiên và nhập cư với tỉ lệ B theo t; giảm do bị lây nhiễm với I(t) theo tỉ lệ β và giảm so chết tự nhiên với tỉ lệ µ:

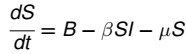
- Hàm E(t): tăng do bị lây nhiễm mới với I(t) theo tỉ lệ β; giảm so chết tự nhiên với tỉ lệ µ; giảm do bệnh nặng lên có thể truyền nhiễm cho người khác với tỉ lệ α và giảm do có khỏi bệnh với tỉ lệ σ:

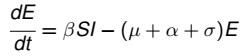
- Hàm I(t) và R(t): Tương tự như trên.

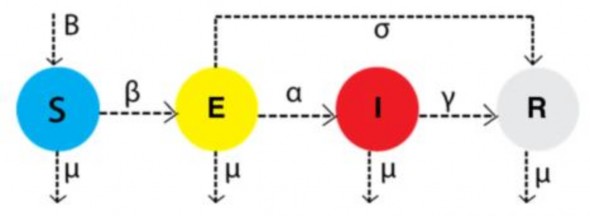
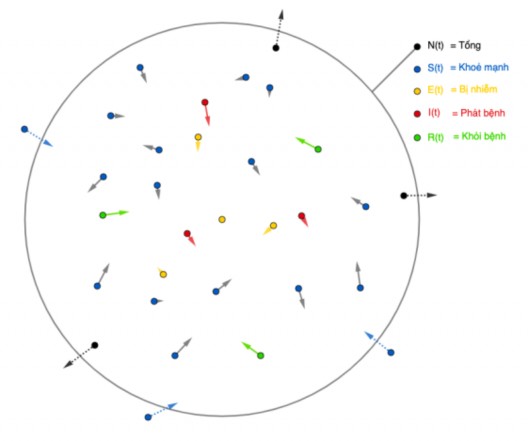
Hình 2.1. Mô hình minh họa quần thể

Ta có hệ phương trình vi phân thường sau đây:

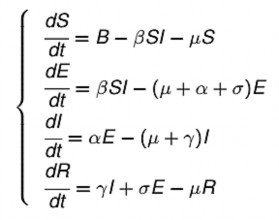
Khi đó, hệ phương trình trên có thể được viết dưới dạng thu gọn như sau: Y’(t) = F(t, Y(t)) .

Đến giai đoạn này, GV đã dẫn dắt SV đi đến hoạt động tiếp theo, đó là sử dụng các phương pháp số trong toán học để giải quyết bài toán hệ phương trình vi phân thường. Áp dụng một số phương pháp giải gần đúng phương trình vi phân thường [43] như phương pháp Euler, phương pháp Euler cải tiến, phương pháp Heun, hoặc phương pháp Runge – Kutta.

Một số đoạn mã chương trình mô phỏng cho các thuật toán trên như sau:

- Phương pháp Euler:

- Phương pháp Euler cải tiến: