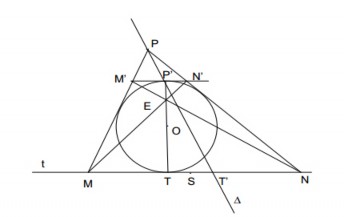
tiếp tuyến với đường tròn (O) cắt t ở M và N. Chứng minh rằng: M,N đối xứng với nhau qua một điểm cố định.
Đáp án
Trước hết ta trình bày lời giải bài toán trên bằng kiến thức của hình học xạ ảnh.
Lời giải 1.
Rõ ràng f: M N là một phép biến đổi xạ ảnh trên t và thuộc loại hypebolic vì nó có hai điểm bất động, trong đó một điểm ở xa vô tận còn một
điểm là trung điểm S của đoạn thẳng TT’ với T’ là giao điểm của và t.
Vì thế f là một phép đồng dạng trên t. Phép đồng dạng này là phép vị tự tâm S tỉ số k. Hơn nữa phép đồng dạng này có tính chất đối hợp nên k = -1. Vậy f là phép đối xứng tâm S. Điều này chứng tỏ M, N đối xứng với nhau qua S cố định (đpcm).
Có thể bạn quan tâm!
-
Kết Quả Khảo Sát Với Giảng Viên -
Tài Liệu Hướng Dẫn Tự Học Cho Sinh Viên -
Dạy học hình học cao cấp ở trường Đại học cho sinh viên sư phạm toán theo hướng chuẩn bị năng lực dạy học hình học ở trường phổ thông - 23
Xem toàn bộ 200 trang tài liệu này.
Với lời giải xạ ảnh trên ta biết được điểm cố định mà M, N đối xứng qua đó chính là trung điểm S của TT’.Từ đó định hướng cho lời giải sơ cấp của bài toán đã cho.
Lời giải 2.
Gọi T ' t và S là trung điểm TT’, suy ra S cố định.
Qua P’ kẻ một đường thẳng song song với t cắt PM, PN lần lượt ở M’ và N’. suy ra MNN’M’ là hình thang ngoại tiếp đường tròn (O).
P ' N ' EN ' M ' N ' P ' N '
Do đó :
MT T ' N MT EM MN T ' N
hay SM = SN
Vậy M và N đối xứng với nhau qua S cố định (đpcm).
Câu 3: Cho bài toán:
Cho hai đường tròn
(O1,R1 ) và
(O2 ,R2 ) ngoài nhau,
R1 R2 . Một đường
tròn (O) thay đổi, tiếp xúc ngoài với (O1,R1 ) tại A, với (O2 ,R2 ) tại B. Chứng minh rằng đường thẳng AB luôn đi qua một điểm cố định.
c) Bài toán trên chứa bất biến của phép biến đổi nào?
- Phép quay.
- Phép tịnh tiến.
- Phép vị tự.
Đáp án: Phép vị tự vì liên quan tới sự thẳng hàng và các đường tròn không bằng nhau.
d) Sử dụng phép biến đổi tương ứng để giải bài toán.
Đáp án:
O
B
I
A
O1
O2
A là tâm vị tự trong biến (O1) thành ( O); B là tâm vị tự biến (O) thành (O2). Khi đó AB qua I là tâm vị tự biến ( O1) thành (O2).( tính chất tích 2 phép vị tự)
V1 là phép vị tự tâm A tỉ số R1/R ; V2 là phép vị tự tâm B, tỉ số R/R2. V1V2 là phép vị tự V tâm I, tỉ số R1/R2. V1V2 (B) = B’ thì A,B,B’ thẳng hàng, mặt khác, V(B) = B’ thì B, B’,I thẳng hàng, hay A, B, I thẳng hàng. Vậy đường thẳng AB luôn qua điểm I cố định.