Định Nghĩa Chuyển Động Tuyệt Đối, Tương Đối Và Chuyển Động Theo

Do (A B )

là véctơ vuông góc với mặt phẳng S, nên vuông góc với. Từ (c)

vBA



A

B

suy ra: A B 

Chú ý 2: Từ cách xác định vận tốc một điểm của vật rắn quay quanh một trục cố định, ta dễ dàng xác định véctơ



vBA

bằng hình học.



vBA

Phương vuông góc với BA Chiều hướng theo chiều quay Trị số vBA = .AB

Hình 1.30

hc hc  ABvB ABvA

(1.37)

Có thể bạn quan tâm!

• Cơ học ứng dụng - 1
• Cơ học ứng dụng - 2
• Khảo Sát Chuyển Động Của Các Điểm Thuộc Vật
• Các Định Lý Hợp Vận Tốc, Hợp Gia Tốc
• Thông Số Làm Việc Chủ Yếu Của Bộ Truyền Bánh Răng
• Lực Liên Kết - Lực Hoạt Động - Phản Lực Liên Kết

Xem toàn bộ 180 trang tài liệu này.

Định lí 2: Hình chiều vận tốc hai điểm bất kì của hình phẳng S chuyển động phẳng lên đường thẳng nối hai điểm đó thì bằng nhau.

Thực vậy:

Chiếu đẳng thức (1.36) lên trục AB ta được:



hcABvB hcABvA hcABvAB

vAB

ABvAB

Do AB , nên hc = 0 vậy định lí được chứng minh

c. Tâm vận tốc tức thời

Định nghĩa: Điểm P trên hình phẳng S mà tại thời điểm khảo sát có vận tốc bằng không, gọi là tâm vận tốc tức thời.

Định lí 3: Ở mỗi thời điểm nếu  0 có một điểm duy nhất thuộc hình phẳng S

có vận tốc bằng không.

Trước hết ta chứng minh sự tồn tại của tâm vận tốc tức thời. Giả sử biết vận tốc



vA và vận tốc góc (Hình 1.31)

Hình 1.31 

Hình 1.32 0

Quay véctơ vA

quanh A theo chiều của đi một góc 90

ta được nửa đường

thẳng AB. Trên AB lấy một điểm P sao cho:

AP 

1

vA



Khi đó:

vPA vA

Mặt khác theo công thức (1.36):



vp vA vPA vA vB  0

Bây giờ ta chứng minh tính duy nhất của tâm P bằng phương pháp phản chứng.

giả sử có hai điểm P1 và P2 mà tại thời điểm khảo sát có tính chất



vp1





vP2

 0 khi đó:



1

2

vp2 vP1 vp p Đó là một điều vô lí vì Vậy: P1  P2.

1

vp p2 .p1 p2  0 .

d. Sự phân bố vận tốc các điểm

Ta xét sự phân bố vận tốc các điểm của tấm phẳng S chuyển động phẳng. Có hai khả năng có thể xảy ra tại môi trương điểm:

Khả năng 1:  0

Lấy tâm vận tốc tức thời P làm cực. Xét vận tốc của một điểm M bất kì thuộc hình phẳng S. Ta có quan hệ vận tốc.



vM vP vMP vMP

Phương vuông góc với MP





vM vMP

Chiều hướng theo chiều 

Trị số

vMP = .MP

Vậy khi

 0 , vận tốc tức thời của hình phẳng S

phân bố giống như S đang quay quanh tâm vận tốc tức thời P với vận tốc góc (Hình 1.32)

Người ta nói rằng hình phẳng S quay tức thời quanh P.

Khả năng 2:  0

Xét vận tốc hai điểm M, N bất kì của hình phẳng S.

Ta có



vM vN vMN

Hình 1.33

Do vMN = MN. = 0, nên vM

vN . Vậy khi  0

, vận tốc tức thời của các điểm của hình phẳng S đều bằng nhau (Hình 1.33).

Người ta nói rằng hình phẳng S chuyển động tịnh tiến tức thời.

Như vậy, tại mỗi thời điểm, hình phẳng S hoặc quay tức thời quanh tâm vận tốc

tức thời P (khi

 0 ) hoặc chuyển động tịnh tiến tức thời (khi =0). Chú ý rằng

chuyển động tức thời của hình phẳng chỉ nói lên tính chất của vận tốc. Tuyệt đối không được từ đó suy ra tính chất của gia tốc.

e. Quy tắc thực hành tìm tâm vận tốc tức thời

Dựa vào các kết quả ở trên đưa ra ở đây một số quy tắc thực hành tìm tâm vận tốc tức thời.

Trường hợp 1: Biết vận tốc điểm A và phương vận tốc điểm B. Hai phương này





không song song với nhau.

Dựa vào tính chất vA PA , vB PB từ A và B ta kẻ tương ứng các đường

vA

vuông góc với và . Giao điểm của chúng là tâm vận tốc P (Hình 1.34a).

vB

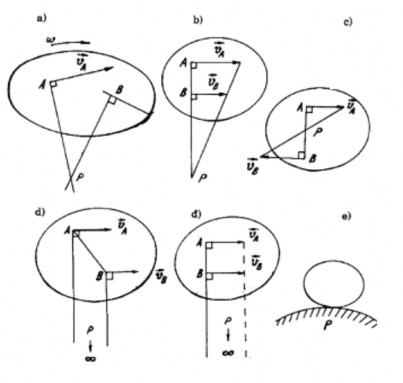
Hình 1.34

Trường hợp 2: Biết vận tốc hai điểm A và B, chúng có phương song song với nhau. Dựa vào tính chất

vA PA vB PB

Ta thấy tâm vận tốc tức thời P chính là giao điểm của đường AB với đường nối

các đầu mút các véctơ vA và vB , (Hình 1.34b và 1.34c). Trường hợp giao điểm ở vô

cùng, tấm phẳng thực hiện chuyển động tịnh tiến tức thời (Hình 1.34d và 1.34đ).

Trường hợp 3: Biết một điểm của hình phẳng có vận tốc bằng không.

Khi chuyển động phẳng là chuyển động lăn không trượt của thiết diện phẳng S trên một đường cố định thì tiếp điểm tiếp xúc có vận tốc tức thời bẳng không. (vì các tiếp điểm của hai vật khi không trượt trên nhau phải có

cùng một vận tốc, mà vật thứ hai cố định). Vì vậy điểm Hình 1.35

của vật tiếp xúc với mặt tựa chính là tâm P (Hình 1.34e).

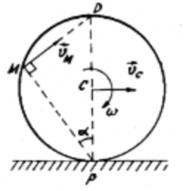
Ví dụ 1.4. Tìm vận tốc của điểm M trên vành của bánh xe bán kính R lăn không

.

v

trượt trên đường thẳng. Cho biết vận tốc tâm C của bánh xe là 

Bài giải

Vì bánh xe lăn không trượt trên đường thẳng, nên điểm tiếp xúc giữa bánh xe và mặt đường là tâm vận tốc tức thời P (Hình 1.35).

Vận tốc góc của bánh xe là:

vc vc

PC R

Vận tốc của điểm M:

vM PM

vc 2R cosR  2v

R c

cos

3. Gia tốc các điểm

a. Biểu thức giải tích xác định gia tốc của một điểm

Đạo hàm biểu thức vận tốc (1.33) ta được:

xBxA

 sin 

 cos

2 cos

 sin B 

yy cos

 sin sin cos

(1.38)

B A 

B 

b. Quan hệ gia tốc giữa hai điểm

Định lý 4: Gia tốc của điểm B tùy ý thuộc hình phẳng S chuyển động phẳng, bằng tổng hình học gia tốc của điểm cực A và gia tốc của điểm B trong chuyển động quay của hình phẳng S quanh A.

n

aB aA aBA aA a BA a BA

(1.39)

Chú ý 1: Từ các hệ thức (1.38) ta có thể nhận được hệ thức (1.39) bằng một vài biến đổi toán học không phức tạp.

Chú ý 2: Từ cách xác định thành phần gia tốc tiếp, gia tốc pháp của một điểm

thuộc vật rắn quay quanh một trục cố định, ta dễ dàng xác định các véc tơ: bằng hình học (Hình 1.36).

a BA , an BA

a BA

Phương AB





Chiều phù hợp với chiều của 

a

BA

Trị số t .AB

an BA 

Hướng từ B đến A

Trong đó:



a

BA

 Trị số n

2

.AB

a AB ;

AB

an

BA

v

BA

Hình 1.36

c. Tâm gia tốc tức thời

Định nghĩa: Điểm Q trên hình phẳng S mà tại thời điểm khảo sát có gia tốc bằng 0 gọi là tâm gia tốc tức thời.

Định lý 5: Ở mỗi thời điểm nếu ω và ε không đồng thời triệt tiêu, có một điểm duy nhất thuộc hình phẳng S có gia tốc bằng 0.

Chứng minh: Sự tồn tại của tâm Q. Giả sử biết

aa ,,,..

Quay véc tơ aa

tg

2

quanh A theo chiều một góc α.

Ta được nửa đường thẳng AB (Hình 7.12). Trên AB lấy một điểm Q sao cho:

AQ 

Như thế:

aA

4 2

aQA aA . Vậy ta có:

Hình 1.37

aQ aA aQA  0

Ta chứng minh sự duy nhất của tâm Q bằng phương pháp phản chứng. Giả sử có hai điểm Q1 và Q2 mà tại thời điểm khảo sát:



Q

Q

a a  0

1 2

Khi đó hệ thức:

aQ aQ aQ Q

2 1 1 2

Là điều vô lý, vì:

aQ Q

 0 . Vậy Q1 Q2

1 2

Chú ý:

- Khi ω và ε không đồng thời triệt tiêu thì Q là một điểm giới nội;

- Khi ω và ε đồng thời triệt tiêu thì Q → ∞;

- Nói chung, tâm vận tốc tức thời P và tâm vận tốc tức thời Q của hình phẳng S không trùng nhau

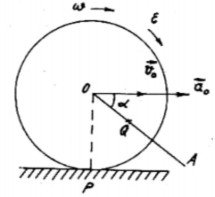
Ví dụ 1.5: Tại một thời điểm nào đó, tâm O của bánh xe lăn không trượt trên đường ray thẳng có vận tốc v0 = 1m/s và gia tốc a0 = 1.5m/s2, (Hình 1.38). Bán kính bánh xe R = 0.5m. Hãy xác định tâm gia tốc tức thời Q tại thời điểm đó.

Bài giải:

Do P là tâm vận tốc tức thời, ta có:

v0  2 / s R

Hình 1.38

Gia tốc góc của bánh xe: a0  3/ s2

R

Chiều của ω và ε cho trên hình 1.38

Quay véc tơ a0

theo chiều của đi một góc α:

tg

2

3 0.75 37o 

4

Ta được nửa đường thẳng OA. Trên đó lấy một điểm Q mà

4 2

OQ ao

 0.4m

Điểm Q đó là tâm gia tốc tức thời.

Chú ý: Khi a0 = 0 thì ε = 0 và do đó α = 0o; OQ = 0. Như vậy khi vận tốc tâm O của bánh xe luôn không đổi thì điểm O đó là gia tốc tức thời.

v0

A

0

vA

600

v

B

B

vBA

Ví dụ 1.6

Tay quay OA có chiều dài r = 0,1 m quay

đều với vận tốc góc

0  30

rad / s . Con trượt

B chuyển động theo phương ngang. Cho chiều

dài của thanh truyền AB là

l r

3 . Tại thời O

điểm đang xét tay quay OA vuông góc với thanh truyền AB (hình 1.39).

Hình 1.39

Hãy: - Xác định vận tốc con trượt B và vận tốc thanh truyền AB.

- Tính gia tốc của con trượt B và gia tốc góc của thanh truyền AB.

Bài giải:

1) Phân tích: Khâu OA chuyển động quay quanh trục cố định O. Thanh truyền AB chuyển động song phẳng, còn con trượt B chuyển động tịnh tiến. Tay quay OA làm với hướng ngang một góc 600.

2) Vận tốc: Tính vận tốc điểm B khi chọn A làm cực:

vB  vA  vBA

(a)

Véc tơ vA có chiều như hình 1.40 và có giá trị:

vA 0OA 0r

Các véc tơ vB và vBA có phương: vB có phương dọc trục Ox còn vBA có phương

vBA cos30  v

A

vuông góc với BA (tức phương AB ):0

Do đó:

vB 

vA

cos 300

0r  2 33

2

m / s

Để tìm giá trị của vBA ta chiếu hai vế của đẳng thức (a) lên phương vuông góc với vB , tức lên phương thẳng đứng:

0  vA cos 60  v cos30

0 0

BA

Từ đó tính được:

cos 60 0

0

vBA  vA cos 300 =vAtg30

0 3

r 3

Vận tốc góc của thanh AB bằng:

vBA

0  10

rad / s

0r 3

BA 3l 3

Tại thời điểm đang xét thanh AB quay thuận chiều kim đồng hồ.

Để tìm vận tốc điểm B cũng có thể sử dụng định lí hình chiếu vận tốc:

0

hcAB vB hcAB vA  vB cos30  vA

Kết quả tìm được trùng với kết quả trên.

Để giải bài toán trên cũng có thể sử dụng phương pháp tâm vận tốc tức thời. Tâm vận tốc tức thời của thanh AB tại thời điểm khảo sát là giao điểm của OA với đường thẳng đứng qua B (hình 1.40).

P

v0

A

0

vA

600

v

B

B

Hình 1.40

vBA

Ta có:

vB 0r 0 

PA ltg600 3 10

rad / s

Vận tốc điểm B được tính theo công thức:

v PB 0

1 2

r3

 3 3

m / s

B 3 cos 6003

Gia tốc của điểm B:

a a at an

B A BA BA

(b)

giá trị:

Thành phần aA

hướng từ A đến O và có

2 2

aA r.0  0,130O

giá trị:

 902

BA

Thành phần an

m / s2

hướng từ B đến A và có

an 2

BA 1020,1 3  10 32

m / s2

BA BA

a

BA

Thành phần t hướng vuông góc với AB tại B, có chiều chưa biết (chọn một

chiều xác định, nếu đáp số dương thì chiều đã chọn là đúng, nếu đáp số âm thì chiều ngược lại với chiều đã chọn) và có trị số:

3

a

BA

t .BA r m / s2

Phương chiều của các véc tơ trong đẳng thức (a) cho trên hình 1.41.

Để tìm giá trị của gia tốc điểm B ta chiếu đẳng thức (b) lên phương AB:

a cos 300 an

Từ đó:

B BA

an 10 32 2 2

aB BA 20m / s

cos 3003

2

Khi chiếu đẳng thức (a) lên phương thẳng đứng (vuông góc với aB ) ta nhận được:

0 an cos300 an cos 600 at sin 600

A BA BA

Từ đó:

at an an tg300  902 102  802

m / s2

BA A BA

Ta dễ dàng tìm được gia tốc của thanh AB:

t

a

 802

 800 32 2

BA

rad / s A

3

BA 0,1 3 

a

Chiều của gia tốc góc n A

a

BA

phù hợp với chiều của t , tại

aBA

thời điểm khảo sát có chiều ngược chiều kim đồng hồ. Thanh O AB tại thời điểm khảo sát chuyển động chậm dần.

Hình 1.41

n t

a

a

BA BA

aB

a

n B

A

1.3. HỢP CHUYỂN ĐỘNG CỦA ĐIỂM- VẬT RẮN

1.3.1. Hợp chuyển động của điểm

1.3.1.1. Khái niệm

1. Mô hình bài toán

Điểm M chuyển động đối với hệ quy chiếu động Oxyz. Thông thường hệ quy chiếu động Oxyz này được gắn liền với một vật S nào đó (Hình 1.42). Hệ quy chiếu động Oxyz chuyển động đối với hệ quy

chiếu cố định O1x1y1z1.

Bài toán đặt ra là khảo sát chuyển động của điểm M đối với hệ quy chiểu Oxyz đang chuyển động đối với hệ quy chiếu O1x1y1z1.

2. Định nghĩa chuyển động tuyệt đối, tương đối và chuyển động theo

a. Chuyển động tuyệt đối

Chuyển động của điểm M đối với hệ

quy chiếu cố định O1x1y1z1 được gọi là

Hình 1.42

chuyển động tuyệt đối. Vận tốc, gia tốc của điểm M trong chuyển động tuyệt đối

Xem tất cả 180 trang.