s s (t)
(1.9)
Biểu diễn quy luật chuyển động của điểm M dọc theo quỹ đạo gọi là phương trình chuyển động của điểm dạng tọa độ tự nhiên.
Chú ý rằng s là một đại lượng đại số. Tuy nhiên nếu chiều chuyển động không đổi và nếu chọn chiều đó là chiều dương để tính cung, thì với cách chọn gốc O thích hợp s sẽ luôn dương.
1.1.3.2. Một vài tính chất hình học của quỹ đạo
1. Hệ tọa độ tự nhiên
Trước hết chúng ta hãy đưa ra
-
O
+
n
M’
b
M
t
t
b
Hình 1.7
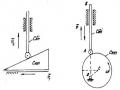
cách xác định mặt phẳng mặt tiếp của n
quỹ đạo tại điểm M của nó. Trên quỹ đạo ngoài điểm M ta lấy thêm điểm M1 (Hình 1.7). Kẻ các tiếp tuyến MT và M1T1. Qua M kẻ đường MT’1// M1T1. Dựng mặt phẳng P chứa các đường MT và MT’1. Khi cho M1 tiến dần đến M, mặt phẳng P sẽ tiến dần đến một mặt
phẳng giới hạn π, gọi là mặt phẳng mật tiếp của quỹ đạo tại điểm M. Như thế, nếu quỹ đạo là đường cong phẳng thì mặt phẳng chứa đường cong quỹ đạo là mặt phẳng mật tiếp tại mọi điểm của quỹ đạo. Khi quỹ đạo là đường cong không gian, ta lấy một cung rất bé MM’ = d s . Vì cung d s rất bé nên có thể thay thế nó bằng một cung phẳng cùng điểm đầu, điểm cuối. Mặt phẳng chứa cung phẳng này sẽ được xem một cách gần đúng là mặt phẳng mật tiếp với quỹ đạo tại điểm M (Hình 1.7).
Dựng trong mặt phẳng mật tiếp với quỹ đạo tại điểm M trục Mt hướng theo tiếp
tuyến của quỹ đạo về phía dương. Véc tơ đơn vị trên trục đó là
t0 . Dựng trục Mn
hướng theo pháp tuyến của quỹ đạo về phía lòm. Pháp tuyến Mn nằm trong mặt phẳng
n0
mật tiếp gọi là pháp tuyến chính. Véc tơ đơn vị trên trục này là . Dựng pháp tuyến
Mb của quỹ đạo tại M và vuông góc với mặt phẳng mật tiếp. Pháp tuyến Mb gọi là
trùng pháp tuyến. Véc tơ đơn vị trên trục này là
b0 . Thường người ta chọn chiều của
b0 sao cho Mtnb tạo thành một hệ trục thuận (Hình 1.7).
Như thế, tại mỗi điểm của đường cong là luôn dựng được một hệ tọa độ vuông
góc có ba trục hướng theo tiếp tuyến, pháp tuyến chính, trùng pháp tuyến, gọi là hệ tọa độ tự nhiên. Hệ tọa độ tự nhiên thay đổi theo vị trí của điểm M trên quỹ đạo và phản ảnh được một phần tính chất hình học của quỹ đạo.
2. Độ cong của quỹ đạo
Ta nhận thấy rằng quỹ đạo càng cong thì tiếp tuyến của nó đổi hướng càng
nhanh dọc theo quỹ đạo ấy. Vì vậy người ta đưa ra khái niệm độ cong của quỹ đạo (Hình 1.8).
Đại lượng: k
tb s
được gọi là độ cong trung bình của quỹ đạo ứng với cung MM1.
Đại lượng:
k lim
d
s 0 s ds
được gọi là độ cong của quỹ đạo tại điểm
M. Đại lượng tại điểm M.
1
k
là bán kính cong của quỹ đạo
Để minh họa, xét quỹ đạo là đường tròn bán kính R. Khi đó ∆s=R∆φ.
Vậy ta có:
k 1 , R
Hình 1.8
s R
Như thế bán kính cong của đường tròn tại các điểm của chúng chính bằng bán kính cong của đường tròn đó.
1.1.3.3. Vận tốc chuyển động
Để xác định vận tốc v ta sẽ tìm hình chiếu của nó trên các trục của hệ tọa độ tự
nhiên. Vì véc tơ v hướng theo tiếp tuyến quỹ đạo tại M, nên định nghĩa:
v t
v t 0
. Mặt khác theo
v dr
dt
dr ds ds dt
sdr
ds
dr
Trong phần hình học vi phân, người ta chứng minh ds
v
vt s; vn vb 0
t0 . Vì vậy ta rút ra:
(1.10)
Chú ý rằng:
vt
1.1.3.4. Gia tốc chuyển động
Tương tự như phần vận tốc, ta sẽ tìm hình chiếu của véc tơ gia tốc trên các trục của hệ tọa độ tự nhiên:
t n b
a a t0 a n0 a b0
Mặt khác theo định nghĩa:
a dv d v t
vtv tvt tv
dt0 ds
dt dt t 0
t 0 t 0
t ds dt
dt
Trong phần hình học vi phân, người ta đã chứng minh:
0n0 ds
dv v2 n
Vì vậy ta có: a tt0 tn0 a a
dt
Cuối cùng ta rút ra: at
dvt ; an
dt
v2
; ab 0
(1.11)
n
a
a
Từ (1.11) ta thấy gia tốc pháp tuyến
luôn luôn hướng về tâm cong của quỹ đạo,
còn gia tốc tiếp tuyến
thì có thể hướng cùng chiều hoặc ngược chiều với vận tốc v .
Từ các biểu thức (1.11) ta đưa ra một vài nhận xét về ý nghĩa của các thành phần gia tốc.
Từ biểu thức
an v2 /
ta thấy: khi điểm chuyển động nói chung v ≠ 0, do đó
an= 0 khi ρ = ∞. Vậy chỉ trong chuyển động thẳng thì an mới luôn luôn triệt tiêu. Trong chuyển động cong, nói chung a ≠ 0. Như thế gia tốc pháp tuyến phản ứng tính cong của quỹ đạo, do đó đặc trưng cho sự thay đổi về phương của véc tơ vận tốc. Chú ý rằng giá trị của an tỷ lệ với bình phương của vận tốc nên tăng rất nhanh khi giá trị vận tốc tăng.
Từ biểu thức a
dvt
dt
ta rút ra: gia tốc tiếp đặc trưng cho sự biến đổi của vận tốc
về mặt trị số. Nó phản ánh tính đều ( at
động.
1.1.4. Một số chuyển động thường gặp
0 ) hay tính biến đổi ( at
0 ) của chuyển
1.1.4.1. Chuyển động đều: Chuyển động đều của điểm là chuyển động mà vận tốc của nó có trị số không đổi (v = v0 = hằng số).
Nếu chọn chiều chuyển động không đổi của điểm làm chiều dương trên quỹ đạo thì phương trình chuyển động của điểm có dạng:
t
s v0dt s0v0t s0
0
1.1.4.2. Chuyển động biến đổi đều: Chuyển động biến đổi đều của điểm là chuyển động mà thành phần gia tốc tiếp luôn có trị số không đổi (at = a = hằng số).
Từ biểu thức a
dvt a; ta suy ra: v
dt t
at v0
Vậy phương trình chuyển động có dạng:
v ds s 1 at 2 v t s
t dt
2 0 0
Trong chuyển động biến đổi đều nếu vt và at cùng dấu thì chuyển động là nhanh dần đều, nếu vt và at ngược dấu nhau thì chuyển động là chậm dần đều. Trong thực tế,
nếu ta chọn chiều dương trên quỹ đạo trùng với chiều của vận tốc đầu v0
thì nếu
at a 0
chuyển động là nhanh dần đều, còn
at a 0
chuyển động là chậm dần
đều cho đến khi dừng lại (v = 0).
Ví dụ 1.2. Cho điểm chuyển động theo quy luật:
x t sin t;
y 1 cost;
z 4sin t
2
Xác định bán kính cong của quỹ đạo theo thời gian t.
Bài giải:
Trước hết đạo hàm các hàm x, y, z theo t:
x 1 cost;
x sin t;
Ta dễ dàng tính được:
y sin t;
y cost;
t
z 2cos ;
2
t
z sin ; 2
t
2
v x2 y 2
z 2
2(1 cost) 4cos2 4
2
a2 x2
y 2
z 2
1 sin 2t
2
Từ đó suy ra:
at
dv 0;
dt
a n v 4
2
1 sin 2 t
2
Do an = a nên ta có: 4
Ví dụ 1.3. Một chất điểm chuyển động trên một đoạn cung của đường tròn có bán kính R = 1000m với vận tốc ban đầu v0 = 54 km/h. Sau khi đi được một đoạn đường có chiều dài 500m, vận tốc của chất điểm giảm xuống còn 36 km/h. Cho biết chất điểm chuyển động chậm dần đều.
Tính gia tốc của chất điểm tại lúc xuất phát và lúc vận tốc có giá trị 36 km/h.
Bài giải:
Chọn chiều dương quỹ đạo thuận chiều chuyển động của chất điểm và chọn gốc toạ độ trùng với vị trí xuất phát của chất điểm (s0 = 0).
Vì chất điểm chuyển động chậm dần đều nên ta có:
v at t v ; s 1 at t 2 v t
0 20
Trong đó: at là gia tốc tiếp tuyến của chất điểm. Khử t từ hai phương trình trên, ta có:
at (v0 v)(v0 v)
2s
Khi thay các giá trị: v0 = 15 m/s (ứng với 54 km/h), v = 10 m/s (ứng với 36 km/h), s = 500m, ta nhận được:
at 5 25 0,125 m / s2
1000
Vì chuyển động là chậm dần đều nên gia tốc tiếp có giá trị như nhau tại mọi thời điểm (at = 0,125 m/s2), còn gia tốc pháp được tính theo công thức (1.11)
- Gia tốc pháp tại thời điểm xuất phát:
a
0
n v2
0 R
152
1000
0,225 m / s 2
- Gia tốc pháp tại thời điểm vận tốc có giá trị 36 km/h:
2
an v
R
102
1000
0,1m / s 2
0,1252 0,2252
Vậy gia tốc toàn phần tại hai thời điểm này là:
(at )2 (an )2
0
0
a0
0,258 m / s 2
(at )2 (a n )2
0,1252 0,12
a 0,16m / s 2
1.2. ĐỘNG HỌC VẬT RẮN TUYỆT ĐỐI
1.2.1. Các chuyển động cơ bản của vật rắn
1.2.1.1. Chuyển động tịnh tiến
1. Định nghĩa
Chuyển động tịnh tiến của vật rắn là chuyển động mà mỗi đoạn thẳng thuộc vật luôn luôn song song với vị trí ban đầu của nó.
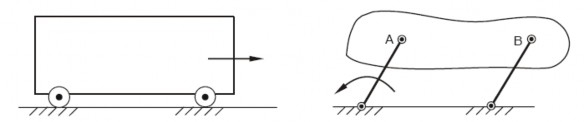
Ví dụ. Chuyển động của thùng xe trên đoạn đưởng thẳng (Hình 1.9), chuyển động của thanh truyền AB trong cơ cấu bốn khâu có các tay quay O1A và O2B bằng nhau (Hình 1.10) là chuyển động tịnh tiến.
Hình 1.9 Hình 1.10
Chú ý: Không có khái niệm điểm chuyển động tịnh tiến. Khi vật rắn chuyển động tịnh tiến, các điểm thuộc vật có thể chuyển động không thẳng, không đều.
2. Khảo sát chuyển động của vật
Định lí. Khi vật rắn chuyển động tịnh tiến, quỹ đạo, vận tốc, gia tốc các điểm của vật rắn như nhau tại cùng một thời điểm.
Chứng minh. Lấy hai điểm A, B bất kỳ thuộc vật. các véc tơ định vị của chúng thỏa mãn điều kiện (Hình 1.11)
rB rA
AB
(1.12)
Đối với vật rắn bất kỳ, véctơ AB luôn có độ lớn không đổi, đối với chuyển
động tịnh tiến AB luôn có hướng không đổi. Vậy
AB = const.
z
B'
B
r
B
A'
A
O
r
A
y
Phương trình (1.12) chứng tỏ rằng vị trí của điểm B là vị trí của điểm A trượt đi một véctơ
hằng AB . Nếu sự dịch chuyển trên được thực hiện
thì quỹ đạo của điểm A sẽ chồng khít lên quỹ đạo của điểm B. Các quỹ đạo như thế được gọi là như nhau.
Do AB =const nên đạo hàm đẳng thức x
(1.12) theo thời gian, ta có:
Hình 1.11
drB drA
hay V V
dt dt B A
dvB dvA
dt dt
hay aB aA
Từ định lý trên ta thấy rằng, việc khảo sát chuyển động tịnh tiến của vật rắn được đưa về khảo sát chuyển động của một điểm bất kỳ thuộc vật rắn. Phương pháp khảo sát chuyển động của điểm đã được trình bày như trong chương trước.
1.2.1.2. Chuyển động quay của vật rắn quanh trục cố định
1. Định nghĩa
z
I
P
P0
Hình 1.12b |
Có thể bạn quan tâm!
-
 Cơ học ứng dụng - 1
Cơ học ứng dụng - 1 -
 Khảo Sát Chuyển Động Của Các Điểm Thuộc Vật
Khảo Sát Chuyển Động Của Các Điểm Thuộc Vật -
 Định Nghĩa Chuyển Động Tuyệt Đối, Tương Đối Và Chuyển Động Theo
Định Nghĩa Chuyển Động Tuyệt Đối, Tương Đối Và Chuyển Động Theo -
 Các Định Lý Hợp Vận Tốc, Hợp Gia Tốc
Các Định Lý Hợp Vận Tốc, Hợp Gia Tốc
Xem toàn bộ 180 trang tài liệu này.

Chuyển động của vật rắn có hai điểm cố định, do đó có một trục đi qua hai điểm đó cố định, được gọi là chuyển động quay quanh một trục cố định. Trục cố định đó được gọi là trục quay của vật.
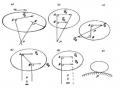
Trên hình 1.12a cho ta mô hình không gian của vật rắn quay quanh một trục cố
định. Giao giữa vật rắn quay và mặt phẳng vuông góc với trục quay cho ta mô hình phẳng như hình vẽ 1.12b.
2. Khảo sát chuyển động của vật
a. Phương trình chuyển động
P0
P
Ta chọn quy ước một chiều quay dương quanh trục. Dựng
mặt phẳng P0 cố định qua trục và mặt phẳng động P qua trục và z
gắn chặt với vật rắn. Góc giữa mặt phẳng P0 và mặt phẳng P và
. Vị trí của vật rắn khi đó được xác định vởi vị trí của mặt phẳng P đối với mặt phẳng P0 tức là được xác định bởi góc quay giữa . Khi vật quay, góc quay thay đổi theo thời gian.
(t) (1.13)
Phương trình (1.13) là phương trình chuyển động của vật rắn quay quanh một trục cố định.
Như thế, vị trí của vật rắn quay quanh một trục cố định được xác định bởi một tham số là góc quay . Do đó vật rắn loại này có một bậc tự do.
Hình 1.13
Chú ý: Góc quay có thể dương hay âm tùy thuộc vào chiều quay dương đã chọn. Thông thường người ta quy ước góc quay được xem là dương nếu vật quay ngược chiều kim đồng hồ, và xem là âm nếu vật quay cùng chiều kim đồng hồ. Góc quay được tính bằng radian (rad).
b. Vận tốc góc của vật
Để đặc trưng cho chuyển động quay của vật rắn quanh một trục cố định, người ta đưa vào các khái niệm vận tốc góc và gia tốc góc.
Đại lượng
d
dt
.
(1.14)
gọi là vận tốc góc của vật.
Như thế vận tốc góc là đạo hàm bậc nhất theo thời gian của góc quay. Dấu của
.
cho biết chiều quay của vật quanh trục. Nếu = > 0 thì tăng theo thời gian và
vật rắn quay theo chiều dương. Ngược lại nếu < 0 thì vật quay theo chiều âm.
Giá trị tuyệt đối
cho biết độ nhanh của chuyển động quay: có giá trị
càng lớn, thì vật quay càng nhanh.
Đơn vị để tính vận tốc góc là radian trên giây. Ký hiệu là rad/s. Người ta cũng dùng đơn vị 1/s để tính vận tốc góc.
Trong kỹ thuật người ta hay sử dụng đơn vị vòng/phút để tính tốc độ góc. Do 1
vòng = 2rad , 1 phút =60s nên ta dễ dàng thiết lập hệ thức liên hệ giữa hai loại đơn vị:
n 0,1n
30
rad / s
(1.15)
Ví dụ: n = 9000 vòng/ph thì
c. Gia tốc của vật
Đại lượng
300
rad / s
d
dt
d 2
dt 2
..
(1.16)
Gọi là gia tốc góc của vật.
Đơn vị để tính gia tốc góc là radian/giây2. Ký hiệu là rad/s2. Người ta cũng dùng đơn vị 1/s2 để tính gia tốc góc.
Gia tốc góc đặc trưng cho sự biến thiên của vận tốc góc theo thời gian.
Khi =0, do đó = const, chuyển động quay đều. Khi 0 , chuyển động quay biến
đổi. Nếu = tăng theo thời gian, thì vật rắn quay nhanh dần. Ngược lại khi giảm theo thời gian, thì vật rắn quay chậm dần. Chú ý rằng sự biến đổi của giá trị vận tốc
góc được đặc trưng bởi sự biến đổi của 22. Do đó để tìm dấu hiệu nhận biết
d 2
tính chất của chuyển động quay, ta xét dấu của đạo hàm:
dt
d 2
2
Do .
dt
Ta có kết luận:
Khi =0: Vật rắn quay đều;
. >0: Vật rắn quay nhanh dần;
. <0: Vật rắn quay chậm dần.
d. Một vài dạng chuyển động quay đặc biệt
- Chuyển động quay đều: Đó là chuyển động quay mà vận tốc góc có trị số
không đổi ( 0 const ). Do đó = 0
Từ đó suy ra: 0 0t 0
= const.
(1.17)
- Chuyển động quay biến đổi đều: Đó là chuyển động quay mà gia tốc góc có trị
số không đổi (
0const ).
dt2 0 t 0 1 t 2 t 2 0 0 0 | (1.18) |
Do d 2 , ta suy ra
e. Véctơ vận tốc góc và véctơ gia tốc góc