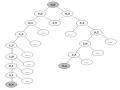
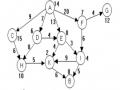
Trạng thái đầu (0;0)
Tập trạng thái đích T={(x, 3) / 0x5} {(3, y) / 0y4}
Quá trình tìm kiếm theo chiều sâu thể hiện theo từng bước sau:
u | Đỉnh kề với u và chưa đánh dấu | L | Father | |
0 | Khởi tạo | (0, 0) | ||
1 | (0, 0) | (5, 0) (0, 4) | (5, 0) (0, 4) | Father(5, 0) =(0, 0) Father(0, 4) =(0, 0) |
2 | (5, 0) | (5, 4), (1, 4) | (5, 4), (1, 4), (0, 4) | Father(5, 4) =(5, 0) Father(1, 4) =(5, 0) |
3 | (5, 4) | (1, 4), (0, 4) | ||
4 | (1, 4) | (1, 4), (4, 0) | ||
5 | (1, 4) | (1, 0) | (1, 0), (4, 0) | Father(1, 0) =(1, 4) |
6 | (1, 0) | (0, 1) | (0, 1), (4, 0) | Father(0, 1) =(1, 0) |
7 | (0, 1) | (5, 1) | (5, 1), (4, 0) | Father(5, 1) =(0, 1) |
8 | (5, 1) | (2, 4) | (2, 4), (4, 0) | Father(2, 4) =(5, 1) |
9 | (2, 4) | (2, 0) | (2, 0), (4, 0) | Father(2, 0) =(2, 4) |
10 | (2, 0) | (0, 2) | (0, 2), (4, 0) | Father(0, 2) =(2, 0) |
11 | (0, 2) | (5, 2) | (5, 2), (4, 0) | Father(5, 2) =(0, 2) |
12 | (5, 2) | (3, 4) | (3, 4), (4, 0) | Father(3, 4) =(5, 2) |
13 | (3, 4) T |
Có thể bạn quan tâm!
-
Hiểu Và Mô Hình Hoá Ngữ Nghĩa Ngôn Ngữ Tự Nhiên -
Mô Tả Không Gian Trạng Thái Bằng Đồ Thị Định Hướng -
Các Chiến Lược Tìm Kiếm Kinh Nghiệm (Tìm Kiếm Heuristic) -
Đồ Thị Và Hoặc Biểu Diễn Toán Tử A B, C, D -
Một Phần Đồ Thị Không Gian Trạng Thái Của Ví Dụ 2.22 -
Đồ Thị Không Gian Trạng Thái Với Hàm Đánh Giá
Xem toàn bộ 272 trang tài liệu này.
Lời giải của bài toán như sau:
(3, 4) (5, 2) (0, 2) (2, 0) (2, 4) (5, 1) (0, 1)
(1, 0) (1, 4) (5, 0) (0, 0)
Ví dụ 2.12: Xét bài toán 8 số, thực hiện tìm kiếm theo chiều sâu với bảng xuất phát A và bảng kết thúc B:
2 | 8 | 3 |
1 | 6 | 4 |
7 | 5 |
2 | 8 | 3 |
6 | 4 | |
1 | 7 | 5 |
Bảng A Bảng B
Bước | u | Đỉnh kề với u và chưa đánh dấu | L | Father | ||||||||||||
0 | Khởi tạo | A | ||||||||||||||
1 | A | 2 | 8 | 3 | 2 | 8 | 3 | 2 | 8 | 3 | D, C, E | Father(C) =A Father(D) =A Father(E) =A | ||||
1 | 4 | 1 | 6 | 4 | 1 | 6 | 4 | |||||||||
7 | 6 | 5 | 7 | 5 | 7 | 5 | ||||||||||
C D E | ||||||||||||||||
2 | D | 2 | 8 | 3 | F, C, E | Father(F) =D | ||||||||||
6 | 4 | |||||||||||||||
1 | 7 | 5 | ||||||||||||||
F | ||||||||||||||||
3 | F=B | C, E | ||||||||||||||
Lời giải của bài toán như sau: BDA
Ví dụ 2.13. Tìm kiếm theo chiều sâu bài toán tháp Hà Nội với n=3
u | Đỉnh kề với u và chưa đánh dấu | L | Father | |
0 | Khởi tạo | (1, 1, 1) | ||
1 | (1, 1, 1) | (1, 1, 2) | (1, 1, 3), (1, 1, 2) | Father(1, 1, 2)=(1, 1, 1) |
(1, 1, 3) | Father(1, 1, 3)=(1, 1, 1) | |||
2 | (1, 1, 3) | (1, 1, 2) | (1, 2, 3), (1, 1, 2) | Father(1, 1, 2)=(1, 1, 3) |
(1, 2, 3) | Father(1, 2, 3)=(1, 1, 3) | |||
3 | (1, 2, 3) | (1, 2, 1) | (1, 2, 2), (1, 2, 1), | Father(1, 2, 1)=(1, 2, 3) |
(1, 2, 2) | (1, 1, 2) | Father(1, 2, 2)=(1, 2, 3) | ||
4 | (1, 2, 2) | (3, 2, 2) | (3, 2, 2), (1, 2, 1), (1, 1, 2) | Father(3, 2, 2)=(1, 2, 2) |
5 | (3, 2, 2) | (3, 2, 3) | (3, 2, 1), (3, 2, 3), | Father(3, 2, 1)=(3, 2, 2) |
(3, 2, 1) | (1, 2, 1), (1, 1, 2) | Father(3, 2, 3)=(3, 2, 2) | ||
6 | (3, 2, 1) | (3, 3, 1) | (3, 3, 1), (3, 2, 3), (1, 2, 1), (1, 1, 2) | Father(3, 3, 1)=(3, 2, 1) |
7 | (3, 3, 1) | (3, 3, 2) | (3, 3, 3), (3, 3, 2), | Father(3, 3, 2)=(3, 3, 1) |
(3, 3, 3) | (3, 2, 3), (1, 2, 1), | Father(3, 3, 3)=(3, 3, 1) | ||
(1, 1, 2) |
Bước | u | Đỉnh kề với u và chưa đánh dấu | L | Father |
8 | (3, 3, 3)T |
Lời giải của bài toán: (1, 1, 1) (1, 1, 3) (1, 2, 3) (1, 2, 2) (3, 2, 2)
(3, 2, 1) (3, 3, 1) (3, 3, 3)
2.4.3. Các trạng thái lặp
Mảng logic DD trong các thuật toán tìm kiếm theo chiều sâu và theo bề rộng đảm bảo cho các đỉnh không được đi qua quá 1 lần trên đường đi đến đích (nếu có). Tuy nhiên, khi không gian trạng thái quá lớn, việc sử dụng mảng DD trong tìm kiếm sẽ bị hạn chế bởi tốc độ tính toán và số phần tử của mảng.
2.4.4. Tìm kiếm sâu lặp
Một giải pháp để tránh phải dùng mảng DD để đánh dấu các đỉnh đã thăm và cho phép một đỉnh có thể thăm nhiều lần, ta tìm kiếm theo độ sâu chỉ tới mức d; nếu không tìm ra nghiệm, ta tăng độ sâu lên d+1 và lại tìm kiếm theo độ sâu tới mức d+1. Quá trình trên được lặp lại với d lần lượt là 1, 2.. đến một độ sâu tối đa max nào đó. Như vậy, thuật toán tìm kiếm sâu lặp (iterative deepening search) sẽ sử dụng thủ tục tìm kiếm sâu hạn chế (depth_limited search) như thủ tục con. Đó là thủ tục tìm kiếm theo độ sâu, nhưng chỉ đi tới độ sâu d nào đó rồi quay lên.
Kỹ thuật tìm kiếm sâu lặp thường được thực hiện khi cây tìm kiếm chứa nhánh vô hạn, và nếu sử dụng tìm kiếm theo độ sâu ta có thể mắc kẹt ở một nhánh nào đó (thuật toán không dừng) và không tìm ra nghiệm.
Trong thủ tục tìm kiếm sâu hạn chế, d là tham số độ sâu, hàm depth ghi lại độ sâu của mỗi đỉnh.
Input: Không gian trạng thái có uo là trạng thái đầu, T là tập trạng thái kết thúc.
Output: Tìm kiếm thành công (có đường đi từ uo đến một trạng thái kết thúc) với độ sâu không quá d hoặc thất bại.
Procedure Depth_Limited_Search(d) Begin
1. Khởi tạo danh sách L chỉ chứa trạng thái ban đầu uo; depth(uo) 0;
2. Loop do
2.1 if L rỗng then
{thông báo thất bại; stop};
End;
2.2 Loại trạng thái u ở đầu danh sách L;
2.3 if u là trạng thái kết thúc then
{thông báo thành công; stop};
2.4 if depth(u) < d then
for mỗi trạng thái v kề u do
{Đặt v vào đầu danh sách L; depth(v) depth(u) + 1};
Input: Không gian trạng thái có uo là trạng thái đầu, T là tập trạng thái kết thúc. Độ sâu tối đa là max.
Output: Tìm kiếm thành công (có đường đi từ uo đến một trạng thái kết thúc) hoặc thất bại.
Procedure Depth_Deepening_Search;
Begin
for d 0 to max do
{Depth_Limited_Search(d) ; if thành công then exit}
End;
Kỹ thuật tìm kiếm sâu lặp kết hợp được các ưu điểm của tìm kiếm theo bề rộng và tìm kiếm theo độ sâu.
- Cũng như tìm kiếm theo bề rộng, tìm kiếm sâu lặp luôn luôn tìm ra nghiệm (nếu bài toán có nghiệm), miễn là ta chọn độ sâu max đủ lớn.
- Tìm kiếm sâu lặp chỉ cần không gian nhớ như tìm kiếm theo độ sâu.
- Trong tìm kiếm sâu lặp, ta phải phát triển lặp lại nhiều lần cùng một trạng thái. Điều đó làm cho ta có cảm giác rằng, tìm kiếm sâu lặp lãng phí nhiều thời gian. Thực ra thời gian tiêu tốn cho phát triển lặp lại các trạng thái là không đáng kể so với thời gian tìm kiếm theo bề rộng. Thật vậy, mỗi lần gọi thủ tục tìm kiếm sâu hạn chế tới mức d, nếu cây tìm kiếm có nhân tố nhánh là b, thì số đỉnh cần phát triển là:
1 + b + b2 +.. + bd
Nếu nghiệm ở độ sâu d, thì trong tìm kiếm sâu lặp, ta phải gọi thủ tục tìm kiếm sâu hạn chế với độ sâu lần lượt là 0, 1, 2, .., d. Do đó các đỉnh ở mức 1 phải phát triển lặp d lần, các đỉnh ở mức 2 lặp d-1 lần, .., các đỉnh ở mức d lặp 1 lần. Như vậy tổng số đỉnh cần phát triển trong tìm kiếm sâu lặp là:
(d+1) 1 + db + (d-1) b2 +.. + 2bd-1 + 1bd Do đó thời gian tìm kiếm sâu lặp là O(bd).
Tóm lại, tìm kiếm sâu lặp có độ phức tạp thời gian là O(bd) (như tìm kiếm theo bề rộng), và có độ phức tạp không gian là O (biểu diễn) (như tìm kiếm theo độ sâu). Nói chung, chúng ta nên áp dụng tìm kiếm sâu lặp cho các vấn đề có không gian trạng thái lớn và độ sâu của nghiệm không biết trước.
Ví dụ 2.13:
Cho đồ thị không gian trạng thái với đỉnh bắt đầu là A, tập đỉnh kết thúc là {E}.
Hình 2.9. Đồ thị không gian trạng thái ví dụ 2.13
Hãy thực hiện tìm kiếm sâu lặp từ đỉnh A đến đỉnh E theo trật tự bảng chữ cái của nhãn các đỉnh với độ sâu max=4.
- Xét d=0: Gọi thủ tục Depth_Limited_Search(0) thì tập đỉnh được tìm thấy là {A}
- Xét d=1: Gọi thủ tục Depth_Limited_Search(1) thì các đỉnh được tìm thấy là
{A, B}
- Xét d=2: Gọi thủ tục Depth_Limited_Search(2) thì các đỉnh được tìm thấy là {A, B, D}
- Xét d=3: Gọi thủ tục Depth_Limited_Search(3) thì các đỉnh được tìm thấy là {A, B, D, A, C} (đỉnh A được xét 2 lần)
- Xét d=4: Gọi thủ tục Depth_Limited_Search(4) thì các đỉnh được tìm thấy là {A, B, D, A, B, C, A, E} (đỉnh A được xét 3 lần, đỉnh B được xét 2 lần).
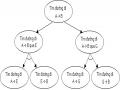
Kết luận: đỉnh E được tìm thấy. Cây tìm kiếm trong ví dụ này là:
Hình 2.10. Các mức tìm kiếm trong cây tìm kiếm ví dụ 2.13
Ví dụ 2.14:
Cho đồ thị không gian trạng thái với đỉnh bắt đầu là A, tập đỉnh kết thúc là {E}.
Hình 2.11. Đồ thị không gian trạng thái ví dụ 2.14
Hãy thực hiện tìm kiếm sâu lặp từ đỉnh A đến đỉnh E theo trật tự tăng dần của nhãn các đỉnh với độ sâu max=3.
- Xét d=0: Gọi thủ tục Depth_Limited_Search(0) thì tập đỉnh được tìm thấy là {A}
- Xét d=1: Gọi thủ tục Depth_Limited_Search(1) thì các đỉnh được tìm thấy là
{A, B, C}
- Xét d=2: Gọi thủ tục Depth_Limited_Search(2) thì các đỉnh được tìm thấy là
{A, B, A, D, C, D}
- Xét d=3: Gọi thủ tục Depth_Limited_Search(3) thì các đỉnh được tìm thấy là
{A, B, A, B, C, } (đỉnh A được xét 2 lần)
- Xét d=4: Gọi thủ tục Depth_Limited_Search(4) thì các đỉnh được tìm thấy là
{A, B, D, A, B, C, A, E} (đỉnh A được xét 3 lần, đỉnh B được xét 2 lần). Kết luận: Không tìm thấy đỉnh E.
Cây tìm kiếm trong ví dụ này là:
Hình 2.12. Các mức tìm kiếm trong cây tìm kiếm ví dụ 2.14
2.4.5.Tìm kiếm trên đồ thị và/hoặc
a) Qui vấn đề về các vấn đề con
Trong mục này chúng ta sẽ nghiên cứu một phương pháp luận để giải quyết vấn đề tìm kiếm dựa trên việc quy vấn đề về các vấn đề con. Quy vấn đề về các vấn đề con (còn gọi là rút gọn vấn đề) là một phương pháp được sử dụng rộng rãi nhất để giải quyết các vấn đề. Trong đời sống hàng ngày, cũng như trong khoa học kỹ thuật, mỗi khi gặp một vấn đề cần giải quyết, ta vẫn thường cố gắng tìm cách đưa nó về các vấn đề đơn giản hơn. Quá trình rút gọn vấn đề sẽ được tiếp tục cho tới khi ta dẫn tới các vấn đề con có thể giải quyết được dễ dàng. Sau đây chúng ta xét một số vấn đề.
1) Vấn đề tính tích phân bất định
Giả sử ta cần tính một tích phân bất định, chẳng hạn (xex + x3) dx. Quá trình chúng ta vẫn thường làm để tính tích phân bất định là như sau. Sử dụng các quy tắc tính tích phân (quy tắc tính tích phân của một tổng, quy tắc tính tích phân từng phần...), sử dụng các phép biến đổi biến số, các phép biến đổi các hàm (chẳng hạn, các phép biến đổi lượng giác)... để đưa tích phân cần tính về tích phân của các hàm số sơ cấp mà chúng ta đã biết cách tính. Chẳng hạn, đối với tích phân (xex + x3) dx, áp dụng quy tắc tích phân của tổng ta đưa về hai tích phân xexdx và x3dx. Áp dụng quy tắc tích phân từng phần ta đưa tích phân xexdx về tích phân exdx. Quá trình trên có thể biểu diễn bởi đồ thị trong hình 2.10.
Các tích phân exdx và x3dx là các tích phân cơ bản đã có trong bảng tích phân. Kết hợp các kết quả của các tích phân cơ bản, ta nhận được kết quả của tích phân đã cho (Hình 2.10)
Hình 2.13. Quy một tích phân về các tích phân cơ bản
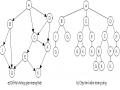
Chúng ta có thể biểu diễn việc quy một vấn đề về các vấn đề con cơ bởi các trạng thái và các toán tử. Ở đây, bài toán cần giải là trạng thái ban đầu. Mỗi cách quy bài toán về các bài toán con được biểu diễn bởi một toán tử, toán tử AB, C biểu diễn việc quy bài toán A về hai bài toán B và C. Chẳng hạn, đối với bài toán tính tích phân bất định, ta có thể xác định các toán tử dạng:
(f1 + f2) dx f1 dx, f2 dx và u dv v du
Các trạng thái kết thúc là các bài toán sơ cấp (các bài toán đã biết cách giải). Chẳng hạn, trong bài toán tính tích phân, các tích phân cơ bản là các trạng thái kết thúc. Một điều cần lưu ý là, trong không gian trạng thái biểu diễn việc quy vấn đề về các vấn đề con, các toán tử có thể là đa trị, nó biến đổi một trạng thái thành nhiều trạng thái khác.
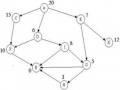
2) Vấn đề tìm đường đi trên bản đồ giao thông
Hình 2.14. Bản đồ nối các thành phố
Bài toán này đã được phát triển như bài toán tìm đường đi trong không gian trạng thái, trong đó mỗi trạng thái ứng với một thành phố, mỗi toán tử ứng với một con đường nối, nối thành phố này với thành phố khác. Bây giờ ta đưa ra một cách biểu diễn khác dựa trên việc quy vấn đề về các vấn đề con. Giả sử ta có bản đồ giao thông