Các Chiến Lược Tìm Kiếm Kinh Nghiệm (Tìm Kiếm Heuristic)

sâu được hình dung như việc khảo sát một cây bắt đầu từ gốc đi theo mọi cành có thể được, khi gặp cành cụt thì quay lại xét cành chưa đi qua.

Trong nhiều vấn đề, dù chúng ta phát triển các trạng thái theo hệ thống nào (theo bề rộng hoặc theo chiều sâu) thì số lượng các trạng thái được sinh ra trước khi ta gặp trạng thái đích thường là cực kỳ lớn. Do đó các thuật toán tìm kiếm mù kém hiệu quả, đòi hỏi rất nhiều không gian và thời gian. Trong thực tế, nhiều vấn đề không thể giải quyết được bằng tìm kiếm mù.

2.2.2. Các chiến lược tìm kiếm kinh nghiệm (tìm kiếm heuristic)

Trong rất nhiều trường hợp, chúng ta có thể dựa vào sự hiểu biết của chúng ta về vấn đề, dựa vào kinh nghiệm, trực giác, để đánh giá các trạng thái. Sử dụng sự đánh giá các trạng thái để hướng dẫn sự tìm kiếm: trong quá trình phát triển các trạng thái, ta sẽ chọn trong số các trạng thái chờ phát triển, trạng thái được đánh giá là tốt nhất để phát triển. Do đó tốc độ tìm kiếm sẽ nhanh hơn. Các phương pháp tìm kiếm dựa vào sự đánh giá các trạng thái để hướng dẫn sự tìm kiếm gọi chung là các phương pháp tìm kiếm kinh nghiệm.

Như vậy chiến lược tìm kiếm được xác định bởi chiến lược chọn trạng thái để phát triển ở mỗi bước. Trong tìm kiếm mù, trạng thái được chọn để phát triển theo thứ tự mà chúng được sinh ra; còn trong tìm kiếm kinh nghiệm việc chọn trạng thái dựa vào sự đánh giá các trạng thái.

2.3. Cây tìm kiếm

Chúng ta có thể nghĩ đến quá trình tìm kiếm như quá trình xây dựng cây tìm kiếm.

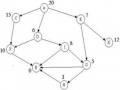
Cây tìm kiếm là cây mà các đỉnh được gắn bởi các trạng thái của không gian trạng thái. Gốc của cây tìm kiếm tương ứng với trạng thái ban đầu. Nếu một đỉnh ứng với trạng thái u, thì các đỉnh con của nó ứng với các trạng thái v. Hình 2.6(a) là đồ thị biểu diễn một không gian trạng thái với trạng thái ban đầu là A, Hình 2.6(b) là cây tìm kiếm tương ứng với không gian trạng thái đó.

Hình 2.6. Đồ thị không gian trạng thái và cây tìm kiếm tương ứng

Mỗi chiến lược tìm kiếm trong không gian trạng thái tương ứng với một phương pháp xây dựng cây tìm kiếm. Quá trình xây dựng cây bắt đầu từ cây chỉ có một đỉnh là trạng thái ban đầu. Giả sử tới một bước nào đó trong chiến lược tìm kiếm, ta đã xây dựng được một cây nào đó, các lá của cây tương ứng với các trạng thái chưa được phát triển. Bước tiếp theo phụ thuộc vào chiến lược tìm kiếm mà một đỉnh nào đó trong các lá được chọn để phát triển. Khi phát triển đỉnh đó, cây tìm kiếm được mở rộng bằng cách thêm vào các đỉnh con của đỉnh đó. Kỹ thuật tìm kiếm theo bề rộng (theo chiều sâu) tương ứng với phương pháp xây dựng cây tìm kiếm theo bề rộng (theo chiều sâu).

2.4. Các chiến lược tìm kiếm mù

2.4.1. Tìm kiếm theo bề rộng

a) Thuật toán

Input: Không gian trạng thái có uo là trạng thái đầu, T là tập trạng thái kết thúc. Output: Tìm kiếm thành công (có đường đi từ uo đến một trạng thái kết thúc) hoặc thất bại. Trong trường hợp tìm kiếm thành công thi đưa ra đường đi.

Procedure Breadth_First_Search; Begin

1. L ={uo}

DD(uo)  true; DD(u) false mọi u khác uo

2. Loop do

2.1. if L =  then

{thông báo tìm kiếm thất bại; stop};

2.2. Loại trạng thái u ở đầu danh sách L;

2.3. if u  T then {thông báo tìm kiếm thành công; stop};

2.4. for (mỗi trạng thái v kề u) and (DD(v) =false) do

End;

{ DD(v)  true;

Đặt v vào cuối danh sách L; Father(v)  u}

Ghi chú:

- Mảng logic DD để đảm bảo mỗi đỉnh không được xét quá 1 lần;

- Mảng Father để tìm lại 1 đường đi trên con đường từ uo đến đích;

- Danh sách L được xử lý như hàng đợi;

- Nếu bài toán có nghiệm (tồn tại đường đi từ trạng thái ban đầu tới trạng thái đích), thì thuật toán tìm kiếm theo bề rộng sẽ tìm ra nghiệm, đồng thời đường đi tìm được sẽ là ngắn nhất (qua ít đỉnh nhất). Trong trường hợp bài toán vô nghiệm và không gian trạng thái hữu hạn, thuật toán sẽ dừng và cho thông báo vô nghiệm.

b) Đánh giá độ phức tạp

Giả sử mỗi trạng thái khi được phát triển sẽ sinh ra b trạng thái kề, b được gọi là nhân tố nhánh. Giả sử nghiệm của bài toán là đường đi có độ dài d. Bởi nhiều nghiệm có thể được tìm ra tại một đỉnh bất kỳ ở mức d của cây tìm kiếm, do đó số đỉnh cần xem xét để tìm ra nghiệm là: 1 + b + b2 +.. + bd-1 + k, trong đó k có thể là 1, 2, .., bd. Do đó số lớn nhất các đỉnh cần xem xét là: 1 + b + b2 +.. + bd

Như vậy, độ phức tạp thời gian của thuật toán tìm kiếm theo bề rộng là O(bd). Độ

phức tạp không gian cũng là O(bd), bởi vì ta cần lưu vào danh sách L tất cả các đỉnh của cây tìm kiếm ở mức d, số các đỉnh này là bd.

c) Ưu và nhược điểm

* Ưu điểm:

Kỹ thuật tìm kiếm theo bề rộng sẽ tìm được lời giải và đường đi tìm được đi qua ít đỉnh nhất (nếu có).

* Nhược điểm:

Không phù hợp với không gian bài toán kích thước lớn. Đối với loại bài toán này, phương pháp tìm kiếm theo bề rộng đối mặt với các thách thức:

+ Cần nhiều bộ nhớ theo số nút cần lưu trữ;

+ Cần nhiều công sức xử lý các nút, nhất là khi các nhánh cây dài làm cho số nút tăng lên;

+ Dễ thực hiện các thao tác không thích hợp, thừa, đưa đến việc tăng đáng kể số nút phải xử lý.

+ Không hiệu quả nếu lời giải ở mức quá sâu trên cây tìm kiếm.

Ví dụ 2.7:

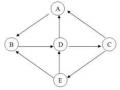
Cho đồ thị biểu diễn không gian trạng thái như sau (Hình 2.7):

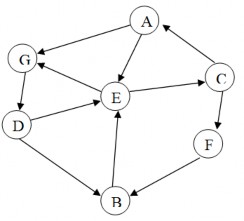
Hình 2.7. Đồ thị không gian trạng thái

Hãy tìm đường đi xuất phát từ trạng thái A đến trạng thái B bằng phương pháp tìm kiếm theo bề rộng theo thứ tự bảng chữ cái của nhãn các đỉnh.

Bước

u	Đỉnh kề với u và chưa đánh dấu	L	Father
0	Khởi tạo		A
1	A	E, G	E, G	Father(E) =A Father(G) =A
2	E	C	G, C	Father(C) =E
3	G	D	C, D	Father(D) =G
4	C	F	D, F	Father(A) =C
5	D	B  T		Father(B) =D

Có thể bạn quan tâm!

• Nhập môn trí tuệ nhân tạo - 2
• Hiểu Và Mô Hình Hoá Ngữ Nghĩa Ngôn Ngữ Tự Nhiên
• Mô Tả Không Gian Trạng Thái Bằng Đồ Thị Định Hướng
• Đồ Thị Không Gian Trạng Thái Ví Dụ 2.13
• Đồ Thị Và Hoặc Biểu Diễn Toán Tử A  B, C, D
• Một Phần Đồ Thị Không Gian Trạng Thái Của Ví Dụ 2.22

Xem toàn bộ 272 trang tài liệu này.

Đường đi tìm được là: B  D  G  A

Ví dụ 2.8:

Bài toán rót nước (xem Ví dụ 2.4) với bình A có dung tích 5 lít, bình B có dung tích 4 lít, yêu cầu đong được 3 lít nước.

Trạng thái đầu (0;0)

Tập trạng thái đích T={(x, 3) / 0x5} {(3, y) / 0y4} Quá trình tìm kiếm theo bề rộng thể hiện theo từng bước sau:

Bước

u	Đỉnh kề với u và chưa đánh dấu	L	Father
0	Khởi tạo		(0, 0)
1	(0, 0)	(5, 0) (0, 4)	(5, 0) (0, 4)	Father(5, 0) =(0, 0) Father(0, 4) =(0, 0)

Bước	u	Đỉnh kề với u và chưa đánh dấu	L	Father
2	(5, 0)	(5, 4), (1, 4)	(0, 4), (5, 4), (1, 4)	Father(5, 4) =(5, 0) Father(1, 4) =(5, 0)
3	(0, 4)	(4, 0)	(5, 4), (1, 4), (4, 0)	Father(4, 0) =(0, 4)
4	(5, 4)		(1, 4), (4, 0)
5	(1, 4)	(1, 0)	(4, 0), (1, 0)	Father(1, 0) =(1, 4)
6	(4, 0)	(4, 4)	(1, 0), (4, 4)	Father(4, 4) =(4, 0)
7	(1, 0)		(4, 4)
8	(4, 4)	(5, 3)	(5, 3)	Father(5, 3) =(4, 4)
9	(5, 3) T

Vì vậy có được lời giải như sau:

(0, 0)  (0, 4)  (4, 0)  (4, 4)  (5, 3)

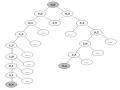
Ví dụ 2.9: Xét bài toán 8 số, thực hiện tìm kiếm theo bề rộng với bảng xuất phát A và bảng kết thúc B:

2	8	3
1	6	4
7		5

2	8	3
	6	4
1	7	5

Bảng A Bảng B

Bước

u	Đỉnh kề với u và chưa đánh dấu													L	Father
0		Khởi tạo													A
1	A		2	8	3		2	8	3		2	8	3		C, D, E	Father(C) =A Father(D) =A Father(E) =A
			1		4		1	6	4		1	6	4
			7	6	5			7	5		7	5
		C D E
2	C		2	8	3		2		3		2	8	3		D, E, F, G, H	Father(F) =C Father(G) =C Father(H) =C
				1	4		1	8	4		1	4
			7	6	5		7	6	5		7	6	5
		F G H
3	D		2	8	3										E, F, G, H, I	Father(I) =D
				6	4
			1	7	5
		I
4	E		2	8	3										F, G, H, I, J	Father(J) =E
			1	6
			7	5	4

Bước	u	Đỉnh kề với u và chưa đánh dấu									L	Father
		J
5	F			8	3		2	8	3		G, H, I, J, K, L	Father(K) =F Father(L) =F
			2	1	4		7	1	4
			7	6	5			6	5
		K L
6	G			2	3		2	3			H, I, J, K, L, M, O	Father(M) =G Father(O) =G
			1	8	4		1	8	4
			7	6	5		7	6	5
		M O
7	H		2	8			2	8	3		I, J, K, L, M, O, P, Q	Father(P) =H Father(Q) =H
			1	4	3		1	4	5
			7	6	5		7	6
		P Q
8	I=B

Vậy lời giải của bài toán là: B  D  A

2.4.2. Tìm kiếm theo chiều sâu

a) Thuật toán

Input: Không gian trạng thái có uo là trạng thái đầu, T là tập trạng thái kết thúc.

Output: Tìm kiếm thành công (có đường đi từ uo đến một trạng thái kết thúc) hoặc thất bại. Trong trường hợp tìm kiếm thành công thi đưa ra đường đi.

Procedure Depth_First_Search Begin

1. L ={ uo};

DD(uo)  true; DD(u) false mọi u khác uo

2. Loop do

2.1. if L =  then

{thông báo tìm kiếm thất bại; stop};

2.2. Loại trạng thái u ở đầu danh sách L;

2.3. if u  T then {thông báo tìm kiếm thành công; stop};

2.4. for (mỗi trạng thái v kề u) and (DD(v) =false) do

{ DD(v)  true;

Đặt v vào đầu danh sách L; Father(v)  u}

End;

Ghi chú:

- Mảng logic DD để đảm bảo mỗi đỉnh không được xét quá 1 lần;

- Mảng Father để tìm lại 1 đường đi trên con đường từ uo đến đích;

- Danh sách L được xử lý như ngăn xếp.

- Thuật toán tìm kiếm theo chiều sâu là hoàn toàn tương tự như thuật toán tìm kiếm theo bề rộng, chỉ có một điều khác là, ta xử lý danh sách L các trạng thái chờ phát triển không phải như hàng đợi mà như ngăn xếp. Cụ thể là trong bước 2.4 của thuật toán tìm kiếm theo bề rộng, ta cần sửa lại là"Đặt v vào đầu danh sách L”.

Sau đây chúng ta sẽ đưa ra các nhận xét so sánh hai chiến lược tìm kiếm mù:

Thuật toán tìm kiếm theo bề rộng luôn luôn tìm ra nghiệm nếu bài toán có nghiệm. Song không phải với bất kỳ bài toán có nghiệm nào thuật toán tìm kiếm theo độ sâu cũng tìm ra nghiệm. Nếu bài toán có nghiệm và không gian trạng thái hữu hạn thì thuật toán tìm kiếm theo độ sâu sẽ tìm ra nghiệm. Tuy nhiên, trong trường hợp không gian trạng thái vô hạn (chẳng hạn như độ thị trạng thái chứa chu trình), thì có thể nó không tìm ra nghiệm, lý do là nếu ta đi theo một nhánh vô hạn mà nghiệm không nằm trên nhánh đó thì thuật toán sẽ không dừng. Do đó không nên áp dụng tìm kiếm theo dộ sâu cho các bài toán có cây tìm kiếm chứa các nhánh vô hạn.

b) Đánh giá độ phức tạp của thuật toán tìm kiếm theo độ sâu

Giả sử rằng, nghiệm của bài toán là đường đi có độ dài d, cây tìm kiếm có nhân tố nhánh là b và có chiều cao là d. Có thể xảy ra, nghiệm là đỉnh ngoài cùng bên phải trên mức d của cây tìm kiếm, do đó độ phức tạp thời gian của tìm kiếm theo độ sâu trong trường hợp xấu nhất là O(bd), tức là cũng như tìm kiếm theo bề rộng. Tuy nhiên, trên thực tế đối với nhiều bài toán, tìm kiếm theo độ sâu thực sự nhanh hơn tìm kiếm theo bề rộng. Lý do là tìm kiếm theo bề rộng phải xem xét toàn bộ cây tìm kiếm tới mức d-

1, rồi mới xem xét các đỉnh ở mức d. Còn trong tìm kiếm theo độ sâu, có thể ta chỉ cần xem xét một bộ phận nhỏ của cây tìm kiếm thì đã tìm ra nghiệm.

Để đánh giá độ phức tạp không gian của tìm kiếm theo độ sâu ta có nhận xét rằng, khi ta phát triển một đỉnh u trên cây tìm kiếm theo độ sâu, ta chỉ cần lưu các đỉnh chưa được phát triển mà chúng là các đỉnh con của các đỉnh nằm trên đường đi từ gốc tới đỉnh u. Như vậy đối với cây tìm kiếm có nhân tố nhánh b và độ sâu lớn nhất là d, ta chỉ cần lưu ít hơn db đỉnh. Do đó độ phức tạp không gian của tìm kiếm theo độ sâu là O(db), trong khi đó tìm kiếm theo bề rộng đòi hỏi không gian nhớ O(bd)!

c) Ưu và nhược điểm của phương pháp tìm kiếm sâu

*Ưu điểm

- Nếu bài toán có lời giải, và không gian trạng thái là hữu hạn thì phương pháp tìm kiếm sâu bảo đảm tìm ra lời giải.

- Kỹ thuật tìm kiếm sâu tập trung vào đích, con người cảm thấy hài lòng khi các câu hỏi tập trung vào vấn đề chính.

- Do cách tìm của kỹ thuật này, nếu lời giải ở rất sâu, kỹ thuật tìm sâu có thể sẽ tiết kiệm thời gian.

* Nhược điểm

Không phù hợp với không gian bài toán lớn, kỹ thuật tìm kiếm sâu có thể không đến lời giải trong khoảng thời gian vừa phải.

d) Ví dụ

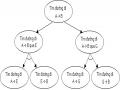
Ví dụ 2.10: Cho đồ thị biểu diễn không gian trạng thái như Hình 2.8.

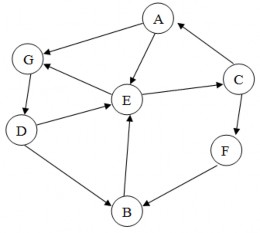
Hình 2.8. Đồ thị không gian trạng thái

Hãy tìm đường đi xuất phát từ trạng thái A đến trạng thái B bằng phương pháp tìm kiếm theo chiều sâu theo thứ tự tăng dần của nhãn các đỉnh.

Bước

u	Đỉnh kề với u và chưa đánh dấu	L	Father
0	Khởi tạo		A
1	A	E, G	G, E	Father(E) =A Father(G) =A
2	G	D	D, E	Father(D) =G
3	D	B	B, E	Father(B) =D
4	B  T

Đường đi tìm được là: B  D  G  A

Ví dụ 2.11:

Bài toán đong nước với bình A có dung tích 5 lít, bình B có dung tích 4 lít, yêu cầu đong được 3 lít nước