so sánh với các giá trị tính toán thực tế khi RR xảy ra để xem xét giá trị chênh lệch trong giới hạn cho phép hay vượt quá giới hạn cho phép.
Bước 2: Xác định xác suất xảy ra của các RR, tác động của RR này đối với các chỉ tiêu như thời gian, chi phí, chất lượng và các chỉ tiêu khác.
Bước 3: Tính toán mức độ ưu tiên rủi ro được tính bằng cách nhân xác suất xảy ra của rủi ro và mức độ tác động của những rủi ro này
Mức độ ưu tiên rủi ro = Xác suất xảy ra của rủi ro x Mức độ tác động của RR
Bước 3: Tính toán tổng mức độ rủi ro hay mức độ ưu tiên cho từng chỉ tiêu như chi phí, thời gian thực hiện công trình hay hiệu suất hoạt động của dự án bằng các tổng hợp mức độ rủi ro do từng rủi ro cụ thể gây ra.
Bước 4: So sánh tổng mức độ rủi ro cho từng chỉ tiêu và giá trị chênh lệch cho phép của các chỉ tiêu này. Từ đó có thể xếp hạng thứ tự ưu tiên của các rủi ro.
Công việc ĐGRR có thể được thực hiện với mức độ chi tiết khác nhau, việc này phù thuộc vào loại RR, mục đích của việc đánh giá, các thông tin, dữ liệu và các nguồn lực hiện có của tổ chức. Nhóm QLRR có thể dùng phương pháp định tính, định lượng hoặc kết hợp giữa định tính và định lượng để thực hiện công việc này. Một số công cụ khác sử dụng trong đánh giá rủi ro được trình bày trong bảng 2.7.
Bảng 2.7. Các phương pháp đánh giá rủi ro [27]
Phương pháp đánh giá | Diễn giải | |
Đánh giá rủi ro đơn giản | Định tính | Bức tranh về RR sẽ được thiết lập thông qua các công cụ đơn giản như động não, thảo luận nhóm, ma trận xác suất – tác động. Xác suất xảy ra RR cũng như mức độ tác động thường được đo lường bởi các mức độ như thấp, trung bình, cao và thường không sử dụng phương pháp phân tích RR chính thức nào |
Có thể bạn quan tâm!
-
Các Rủi Ro Liên Quan Đến Yếu Tố Xã Hội -
Khái Niệm Quản Lý Rủi Ro Và Một Số Hướng Dẫn Về Quản Lý Rủi Ro -
Đánh Giá Rủi Ro Thông Qua Ma Trận Xác Suất – Tác Động (Probability – Impact Matrix) -
Phương Pháp Phân Tích Mạng Anp (Analytic Network Process) -
Tình Hình Thực Hiện Dự Án Đsđt Tại Thành Phố Hồ Chí Minh -
Tình Hình Thực Hiện Dự Án Đầu Tư Xây Dựng Đsđt Tuyến Số 1 Thành Phố Hồ Chí Minh – Tuyến Bến Thành – Suối Tiên
Xem toàn bộ 204 trang tài liệu này.
Phương pháp đánh giá | Diễn giải | |
Đánh giá rủi ro chuẩn (standard risk analysis) | Định tính và định lượng | Một số phương pháp được sử dụng để đánh giá RR như phân tích độ nhạy, phân tích kịch bản, phân tích tương quan, ANP/AHP, ma trận RR thường được sử dụng để trình bày kết quả. Phương pháp ANP sẽ được trình bày cụ thể trong phần tiếp theo. |
Đánh giá RR dựa trên các mô hình | Chủ yếu là định lượng | Sử dụng các công cụ như phân tích Monte Carlo, System Dynamics (SDs), cây sự kiện để phân tích các RR. |
2.5. Mô hình phân tích mạng ANP
Phương pháp phân tích mạng ANP là những phương pháp được sử dụng rộng rãi trong việc ra quyết định dưới sự ảnh hưởng của nhiều tiêu chuẩn cho trước. Trước khi thảo luận về phương pháp ANP, mô hình phân tích thứ bậc AHP (Analytic Hierarchy Process) sẽ được phân tích vì nó là nền tảng lý thuyết để phát triển mô hình ANP.
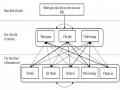
AHP được phát triển bởi Saaty T L [105] trong những thập niên 70s. Đến nay, phương pháp này được áp dụng trong nhiều lĩnh vực như kinh doanh, phân bổ nguồn lực, phân tích và lựa chọn dự án, và ĐGRR. Về cơ bản, phương pháp AHP xác định và sắp xếp một vấn đề cần giải quyết theo một trật tự thứ bậc từ mục tiêu (Goal), đến các tiêu chí (Criteria) và các phương án lựa chọn (Alternatives). Cấu trúc cơ bản của AHP phương pháp được thể hiện ở hình 2.2.
Mục tiêu
Tiêu chí
Các phương án
Mục tiêu
Tiêu chí
Các phương án
Hình 2.2. Cấu trúc cơ bản của mô hình AHP (bên trái) và ANP (bên phải)
Việc xác định cấu trúc của AHP có thể dựa vào nhiều phương pháp như quá trình tư duy, hoặc dựa vào ý kiến chuyên gia hoặc các nghiên cứu đi trước. Giải quyết vấn đề trong phương pháp AHP là việc so sánh cặp giữa các yếu tố để xác định mức độ tác động của mỗi yếu tố trong mô hình AHP dựa vào một bảng phỏng vấn cấu trúc (trình bày chi tiết bên dưới). Nghĩa là, người ra quyết định phải so sánh tầm quan trọng của các tiêu chí đóng góp đến mục tiêu. Tiếp đến, người ra quyết định phải so sánh tầm quan trọng của các phương án đến từng tiêu chí cụ thể. Trong giải quyết vấn đề phức tạp với nhiều cấp độ, việc quyết định mức độ tác động của mỗi yếu tố trong mỗi cấp độ được xác định bằng cách so sánh mức độ tác động của yếu tố trong cấp độ đó đóng góp đến cấp độ trước nó. Saaty T L [105] đề xuất một một bảng phỏng vấn cấu trúc với 9 cấp độ để so sánh mức độ tác động giữa các tiêu chuẩn, các phương án.
Gọi yếu tố cần so sánh tầm quan trọng là x1,….xn, và w1,…,wn là trọng số tầm quan trọng của mỗi yếu tố, so sánh cặp tầm quan trọng có thể biểu diễn dưới dạng ma trận 2.1.
(2.1)
Chú ý rằng:
A (
với
aij ,
aji
1 , và
aij
aii 1
Trong đó, i là yếu tố ở hàng i và j là yếu tố ở cột j, và vì thế aij là tầm quan trọng của yếu tố i so sánh với yếu tố j. Saaty T L và Vargas L G [107] chỉ ra rằng, ma
trận so sánh tầm quan trọng là để xác định trọng số tầm quan trọng cho tất cả các yếu tố trong mô hình. Hiện nay, có nhiều phương pháp để xác định trọng số ưu tiên (priority weights- ma trận w) tầm quan trọng cho tất cả các yếu tố trong mô hình. Phương pháp đơn giản nhất là dùng phương pháp xấp xỉ được tính toán dựa theo các bước và công thức tương ứng dưới đây:
Bước 1: Tổng tất cả các yếu tố trong dòng i:
ri aij
i
(2.2)
Bước 2: Chuẩn hóa các dòng i:
pi
ri
ri
(2.3)
i
Lợi thế của phương pháp này là đơn giản, dễ tính toán và được ứng dụng trong trường hợp ma trận so sánh mức độ tác động (ma trận A) là đồng nhất (thảo luận chi tiết bên dưới). Tuy nhiên, nhược điểm của phương pháp này là không tính toán và kiểm tra được tính đồng nhất của ma trận so sánh cặp (ma trận A), vì thế nó ít được sử dụng.
Một phương pháp được sử dụng rộng rãi để tính toán ma trận trọng số ưu tiên là phương pháp trị số đặc trưng (eigenvalue method). Ma trận trọng số ưu tiên (w) có thể được tính toán dựa vào công thức sau:
Aw max w
(2.4)
Trong đó, A là ma trận so sánh cặp tầm quan trọng dùng bảng phỏng vấn cấu trúc, 9 cấp độ phát triển bởi Saaty T L [105] trong bảng 2.7. w là ma trận trọng số ưu
tiên cần tính toán, hay còn gọi là vector trị số đặc trưng (eigenvectors), và
max
là giá
trị đặc trưng lớn nhất (eigenvalue) của ma trận A. Nếu ma trận A là đồng nhất hoàn hảo, lúc đó max = n (số tiêu chuẩn cần so sánh).
Lợi thế của phương pháp trị số đặc trưng là nó cho phép kiểm tra tính đồng nhất của ma trận so sánh cặp (A). Trị số n - max đo lường mức độ không đồng nhất của ma trận A. Một ma trận so sánh cặp được gọi là đồng nhất nếu nó đảm bảo hai tính chất:
Thứ nhất: Thỏa mãn tính chất bắc cầu:
aij aik akj
(2.5)
Nghĩa là nếu bạn thích phương án A nhiều hơn 2 lần phương án B, và thích
phương án B nhiều hơn 3 lần phương án C. Sau đó, theo tính chất bắc cầu, bạn phải thích phương án A nhiều hơn 6 lần so với phương án C.
Thứ 2: Phải thỏa mãn tính chất đảo ngược:
aij a
(2.6)
1
ji
Tính chất này có nghĩa là nếu bạn thích phương án A nhiều hơn 2 lần phương án B, sau đó tính chất đảo ngược yêu cầu rằng, bạn thích phương án B chỉ bằng ½ so với phương án A.
Nếu một ma trận so sánh cặp giữa các yếu tố (A) thỏa mãn hai tính chất trên thì được gọi là ma trận so sánh cặp đồng nhất. Tuy nhiên, trong thực tế, vì khi có nhiều cấp độ, tiêu chuẩn để so sánh, sự đồng nhất là khó để đảm bảo. Saaty T L [104] đề xuất phương pháp để kiểm tra tính đồng nhất của ma trận so sánh cặp như sau:
Chỉ số nhất quán:
CI max n
n 1
Tỷ lệ nhất quán:
CR CI
RI
(2.7)
(2.8)
Trong đó RI là chỉ số ngẫu nhiên (Random index) được tính toán từ trung bình 500 ma trận của CI được cung cấp ở bảng 2.8.
Bảng 2.8. Chỉ số RI đề xuất bởi Saaty [105]
Saaty T L và Vargas L G [107] chỉ ra rằng, một ma trận so sánh cặp được xem
là đồng nhất nếu chúng có tỷ lệ đồng nhất CR ít hơn 10% (CR 0.1).
Cuối cùng, tổng hợp tất cả các bước để đạt được trọng số tổng thể (global priority weights). Nghĩa là trọng số ưu tiên của tiêu chuẩn sẽ được nhân với trọng số của phương án lựa chọn để đạt được trọng số ưu tiên tổng thể. Phương án được chọn là phương án có trọng số ưu tiên tổng thể lớn nhất.
Nhược điểm của phương pháp phân tích thứ bậc AHP là nó giả sử rằng, các tiêu chí và phương án lựa chọn là độc lập, không phụ thuộc lẫn nhau. Tuy nhiên, trong thực tế, các tiêu chí có thể có mối quan hệ qua lại với nhau hoặc các phương án lựa chọn có thể có quan hệ với ngược lại với tiêu chí. Vì thế, phương pháp ANP, được phát triển dựa trên phương pháp AHP, để giải quyết sự tương tác bên trong và bên ngoài của các yếu tố, tiêu chí, phương án trong mô hình. Sự sự khác biệt giữa AHP và ANP được thể hiện rõ ràng trong hình 2.2 ở trên.
Mục tiêu
Tiêu chí
Tiêu chí nhỏ
Phương án
Mục tiêu
Tiêu chí
Tiêu chí nhỏ
Phương án
ANP là một phương pháp mở rộng của AHP để cho phép các yếu tố trong các cấp độ có phụ thuộc lẫn nhau. Saaty T L [104] phát triển một phương pháp được gọi là các siêu ma trận (supermatrix) để giải quyết vấn đề tương tác và quan hệ giữa các yếu tố trong mô hình. Nói cách khác, siêu ma trận là ma trận tổng hợp thể hiện mối quan hệ tương tác giữa tất cả các yếu tố từ mối quan hệ giữa các mục tiêu với các tiêu, tiêu chí nhỏ với tiêu chí lớn, giữa các mục tiêu, tiêu chí, tiêu chí nhỏ với các phương án được đưa ra. Ví dụ, hình 2.3 dưới đây thể hiện một siêu ma trận giải quyết vấn đề quan hệ và tương tác qua lại giữa các yếu tố trong ANP.
W21 | w22 | ||
W32 | W33 | ||
W34 | I |
Hình 2.3. Cấu trúc cơ bản của một siêu ma trận trong mô hình ANP [104]
Trong hình 2.3, các vector trọng số ưu tiên xác định trong phương pháp ANP ở trên được sắp xếp vào các cột tương ứng với các tiêu chuẩn và các phương án lựa chọn.
+ Ma trận W21 chỉ ra trọng số ưu tiên của các tiêu chí đóng góp đến mục tiêu
+ Ma trận W22 giải thích cho mối quan hệ giữa các tiêu chí với nhau
+ Ma trận W32 trọng số ưu tiên thể hiện sự đóng góp của các tiêu chí nhỏ lên tiêu chí lớn
+ Ma trận W33 thể hiện sự tương tác trong nội bộ các tiêu chuẩn nhỏ
+ Ma trận W34 là ma trận trọng số ưu tiên chỉ ra tầm quan trọng của các tiêu chuẩn nhỏ lên các phương án lựa chọn
Trong ANP, hai loại siêu ma trận cần được xác định, bao gồm: siêu ma trận không trọng số (Unweighted supermatrix) và ma trận trọng số (Weighted supermatrix). Khác biệt với AHP, siêu ma trận đạt được bởi ANP có tổng các trọng số ưu tiên trong mỗi cột của siêu ma trận thường lớn hơn 1. Điều này xuất phát từ sự tương tác và quan hệ giữa các yếu tố trong mô hình ANP. Diễn đạt một cách toán học, siêu ma trận sẽ không thỏa mãn tính chất ma trận ngẫu nhiên (stochastic matrix), một tính chất quan trọng để đạt được trọng số ưu tiên cuối cùng của các phương án. Siêu ma trận mà tổng các trọng số ưu tiên của mỗi cột lớn hơn 1 được gọi là siêu ma trận không trọng số. Vì thế, Saaty T L [106] đề xuất chuẩn hóa ma trận không trọng số theo cột để đạt được ma trận trọng số.
Cuối cùng là để đạt được ma trận so sánh tầm quan trọng tổng thể, bằng cách đạt được ma trận giới hạn (limit matrix). Siêu ma trận giới hạn được thiết lập từ siêu ma trận trọng số bởi nhân nó với chính nó cho đến khi các phần tử theo cột của nó không thay đổi. Các giá trị trong siêu ma trận giới hạn là chỉ số ưu tiên mong muốn của các phần tử trong ma trận có xem xét đến mục tiêu của hệ thống.
AHP là một phương pháp lý thuyết về đo lường nhằm mô hình hóa vấn đề theo thứ bậc từ trên xuống dưới [17]. Tuy nhiên, không phải việc ra quyết định nào cũng có thể phân cấp theo dạng thứ bậc. Có rất nhiều vấn đề, các yếu tố ảnh hưởng không những tác động tới bản chất của vấn đề mà còn tương tác ảnh hưởng lẫn nhau. Việc tương tác giữa các yếu tố có thể xảy ra trong phạm vi cùng một nhóm hoặc giữa các nhóm với nhau. Để giải quyết vấn đề này, phương pháp phân tích mạng ANP được sử dụng.
ANP là phương pháp được xem là phù hợp trong nghiên cứu đánh giá rủi ro dự án bởi một số lý do sau:
Thứ nhất, ưu điểm của ANP so với AHP đó là ANP cho phép phân tích các mối
quan hệ phụ thuộc lẫn nhau giữa các yếu tố nhằm đưa ra các quyết định mang tính chắc chắn hơn [20]. Đối với dự án ĐSĐT, có rất nhiều biến RR và các biến RR này được nhóm gộp thành nhiều nhóm nhỏ. Các nhóm RR này có mức độ ảnh hưởng lên từng mục tiêu dự án như chi phí, thời gian và chất lượng là hoàn toàn khác nhau. Việc sử dụng ANP cho phép tác giả có thể đánh giá tầm quan trọng của các nhóm RR này đối với mục tiêu dự án một cách tổng hợp có tính đến trọng số giữa các mục tiêu. Bên cạnh đó, các biến RR trong từng nhóm cũng có mức độ ảnh hưởng khác nhau đến các mục tiêu và trong nội bộ các nhóm RR cũng tồn tại sự tương tác qua lại lẫn nhau. Do vậy ANP được xem là phương pháp phù hợp nhằm xác định chỉ số mức độ tác động tổng hợp của chúng có tính đến trọng số các mục tiêu của dự án.
Thứ hai, ANP được xem là công cụ phổ biến trong quản lý dự án đầu tư xây dựng nói chung và cụ thể là quản lý rủi ro hiện nay trên thế giới và được nhiều nhà khoa học áp dụng trong nghiên cứu liên quan đến quá trình thực hiện các dự án đầu tư xây dựng. Cụ thể, Meade L M và Presley A [88] đã sử dụng ANP như một phương pháp đánh giá trong việc lựa chọn các dự án. Cheng E W L và Li H [44] đã tính toán mức độ ưu tiên của các dự án xây dựng tiềm năng với 5 mức độ thông qua ANP. Bên cạnh đó, việc lựa chọn các dự án, xác định mức độ ưu tiên của các đề xuất dự án xây dựng bằng ANP cũng được Dikmen I, Birgonul M T và cộng sự [49] sử dụng. Nhiều nhà nghiên cứu đã sử dụng ANP như công cụ đánh giá công tác quản lý tiến độ dự án của các nhà thầu xây dựng [51]. Mavi R K và Standing C [87] đã xác định các yếu tố dẫn đến thành công của một dự án cũng như xác định nguyên nhân và những ảnh hưởng của các yếu tố này đến dự án thông qua ANP. Một số lĩnh vực nghiên cứu khác liên quan đến sử dụng ANP như lựa chọn nhà thầu xây dựng [102]. Almeida M [22] cho rằng lựa chọn nhà thầu có năng lực là việc làm cần thiết vì điều này có thể loại bỏ được một số rủi ro có thể dẫn đến sự thất bại của dự án. Tác giả này nhận định, ANP là một công cụ hỗ trợ cho việc ra quyết định lựa chọn nhà thầu bằng cách xác định mức độ quan trọng của các tiêu chí được sử dụng để lựa chọn nhà thầu. Chen Z, Li H và cộng sự [42] đã ứng dụng mô hình ANP trong đánh giá rủi ro môi trường tổng thể đến dự án đầu tư xây dựng sân bay quốc tế.
Thứ ba, mục đích của ANP là phương pháp sắp xếp thứ tự ưu tiên các lựa chọn (alternatives) dựa vào các tiêu chí cho trước, từ đó giúp đưa ra quyết định phương